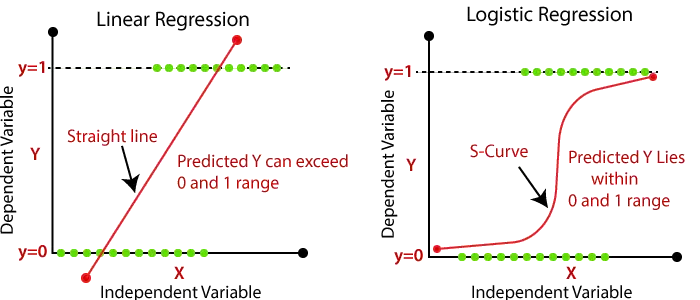
Lineārā regresija un loģistiskā regresija ir divi slavenie mašīnmācīšanās algoritmi, uz kuriem attiecas uzraudzīta mācību tehnika. Tā kā abiem algoritmiem ir uzraudzīts raksturs, šie algoritmi prognožu veikšanai izmanto marķētu datu kopu. Bet galvenā atšķirība starp tām ir tā, kā tās tiek izmantotas. Lineāro regresiju izmanto regresijas problēmu risināšanai, savukārt loģistisko regresiju izmanto klasifikācijas problēmu risināšanai. Tālāk ir sniegts abu algoritmu apraksts kopā ar atšķirību tabulu.
Lineārā regresija:
- Lineārā regresija ir viens no vienkāršākajiem mašīnmācīšanās algoritmiem, kas ietilpst uzraudzītās mācīšanās tehnikā un tiek izmantots regresijas problēmu risināšanai.
- To izmanto nepārtraukta atkarīgā mainīgā prognozēšanai ar neatkarīgu mainīgo palīdzību.
- Lineārās regresijas mērķis ir atrast vislabāko atbilstības līniju, kas var precīzi paredzēt nepārtrauktā atkarīgā mainīgā izvadi.
- Ja prognozēšanai izmanto vienu neatkarīgu mainīgo, tad to sauc par vienkāršu lineāro regresiju, un, ja ir vairāk nekā divi neatkarīgi mainīgie, tad šādu regresiju sauc par vairāku lineāro regresiju.
- Atrodot vispiemērotāko līniju, algoritms nosaka attiecības starp atkarīgo mainīgo un neatkarīgo mainīgo. Un attiecībām jābūt lineārām.
- Lineārās regresijas izvadei jābūt tikai tādām nepārtrauktām vērtībām kā cena, vecums, alga utt. Atkarīgo mainīgo un neatkarīgo mainīgo attiecību var parādīt zemāk esošajā attēlā:

Augšējā attēlā atkarīgais mainīgais atrodas uz Y ass (alga) un neatkarīgais mainīgais ir uz x ass (pieredze). Regresijas līniju var uzrakstīt šādi:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Kur0un a1ir koeficienti un ε ir kļūdas termins.
Loģistiskā regresija:
- Loģistiskā regresija ir viens no populārākajiem mašīnmācīšanās algoritmiem, kas ietilpst uzraudzītās mācīšanās paņēmienos.
- To var izmantot klasifikācijas, kā arī regresijas problēmām, bet galvenokārt izmanto klasifikācijas problēmām.
- Loģistisko regresiju izmanto, lai prognozētu kategoriski atkarīgo mainīgo ar neatkarīgu mainīgo palīdzību.
- Loģistikas regresijas problēmas rezultāts var būt tikai no 0 līdz 1.
- Loģistisko regresiju var izmantot, ja ir vajadzīgas varbūtības starp divām klasēm. Piemēram, vai šodien līs vai nē, 0 vai 1, patiess vai nepatiess utt.
- Loģistiskās regresijas pamatā ir maksimālās iespējamības novērtējuma koncepcija. Saskaņā ar šo aplēsi novērotajiem datiem jābūt visticamākajiem.
- Loģistikas regresijā ievades svērto summu nododam caur aktivizācijas funkciju, kas var kartēt vērtības no 0 līdz 1. Šāda aktivizācijas funkcija ir pazīstama kā sigmoīdā funkcija un iegūto līkni sauc par sigmoīdo līkni vai S-līkni. Apsveriet tālāk redzamo attēlu:

- Loģistiskās regresijas vienādojums ir:

Atšķirība starp lineāro regresiju un loģistisko regresiju:
| Lineārā regresija | Loģistiskā regresija |
|---|---|
| Lineāro regresiju izmanto, lai prognozētu nepārtrauktu atkarīgo mainīgo, izmantojot noteiktu neatkarīgu mainīgo kopu. | Loģistisko regresiju izmanto, lai prognozētu kategoriski atkarīgo mainīgo, izmantojot noteiktu neatkarīgu mainīgo kopu. |
| Regresijas problēmas risināšanai izmanto lineāro regresiju. | Loģistisko regresiju izmanto klasifikācijas problēmu risināšanai. |
| Lineārajā regresijā mēs prognozējam nepārtraukto mainīgo vērtību. | Loģistikas regresijā mēs prognozējam kategorisko mainīgo vērtības. |
| Lineārajā regresijā mēs atrodam vislabāk atbilstošo līniju, ar kuras palīdzību mēs varam viegli paredzēt rezultātu. | Loģistikas regresijā mēs atrodam S līkni, pēc kuras mēs varam klasificēt paraugus. |
| Precizitātes noteikšanai tiek izmantota mazākā kvadrāta novērtējuma metode. | Precizitātes novērtēšanai tiek izmantota maksimālās varbūtības aplēses metode. |
| Lineārās regresijas izvadei ir jābūt nepārtrauktai vērtībai, piemēram, cenai, vecumam utt. | Loģistikas regresijas izvadei ir jābūt kategoriskajai vērtībai, piemēram, 0 vai 1, Jā vai Nē utt. |
| Lineārajā regresijā ir nepieciešams, lai attiecība starp atkarīgo mainīgo un neatkarīgo mainīgo būtu lineāra. | Loģistiskajā regresijā nav nepieciešama lineāra sakarība starp atkarīgo un neatkarīgo mainīgo. |
| Lineārās regresijas gadījumā starp neatkarīgiem mainīgajiem var būt kolinearitāte. | Loģistiskajā regresijā starp neatkarīgo mainīgo nedrīkst būt kolinearitāte. |
