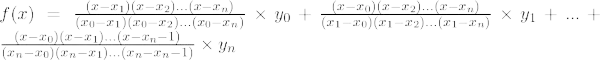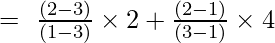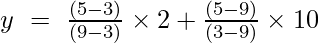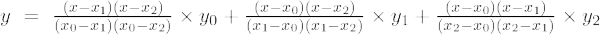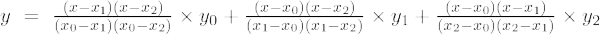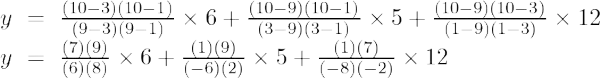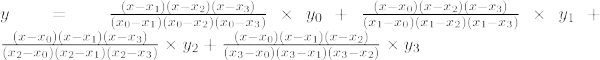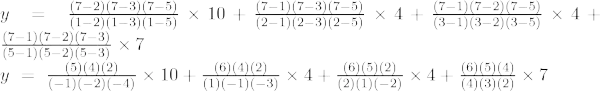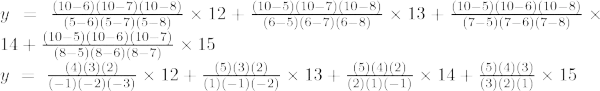logo

TechCodeview

Lagranža interpolācijas formula

Lagranža interpolācijas formula atrod polinomu ar nosaukumu Lagranža polinoms, kas iegūst noteiktas vērtības patvaļīgā punktā. Tā ir n-tā pakāpe funkcijas f(x) polinoma izteiksme. Interpolācijas metode tiek izmantota, lai atrastu jaunus datu punktus zināmu datu punktu diskrētas kopas diapazonā.

Šajā rakstā mēs detalizēti uzzināsim par Lagranža interpolāciju, Lagranža interpolācijas formulu, Lagranža interpolācijas formulas pierādījumu, piemēriem, kuru pamatā ir Lagranža interpolācijas formula, un citiem.



Kas ir Lagranža interpolācija?

Lagranža interpolācija ir veids, kā atrast jebkuras funkcijas vērtību jebkurā noteiktā punktā, kad funkcija nav dota. Mēs izmantojam citus funkcijas punktus, lai iegūtu funkcijas vērtību jebkurā vajadzīgajā punktā.

Pieņemsim, ka mums ir funkcija y = f(x), kurā, aizstājot x vērtības, tiek iegūtas dažādas y vērtības. Un mums tiek doti divi punkti (x1, un1) un (x2, un2) uz līknes, tad y vērtību pie x = a(konstante) aprēķina, izmantojot Lagranža interpolācijas formulu.

Lagranža interpolācijas formula

Dotas dažas reālās vērtības x1, x2, x3, …, xnun y1, un2, un3, …, unnun būs polinoms P ar reāliem koeficientiem, kas atbilst nosacījumiem P(xi) = uni, ∀ i = {1, 2, 3, …, n} un polinoma P pakāpei jābūt mazākai par reālo vērtību skaitu, t.i., pakāpi (P)



Lagranža interpolācijas formula n-tajai kārtībai

Lagranža interpolācijas formula nthpakāpes polinoms ir norādīts zemāk:

Lagranža interpolācijas formula n th kārtība ir,

f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} imes y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n



Lagranža pirmās kārtas interpolācijas formula

Ja Polinoma pakāpe ir 1, tad to sauc par pirmās kārtas polinomu. Lagranža interpolācijas formula 1stpolinomu secība ir,

f(x)~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Lagranža otrās kārtas interpolācijas formula

Ja polinoma pakāpe ir 2, tad to sauc par otrās kārtas polinomu. Lagranža interpolācijas formula otrās kārtas polinomiem ir,

f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Lagranža teorēmas pierādījums

Apskatīsim dotās formas n-tās pakāpes polinomu,

f(x) = A0(x–x1)(x–x2)(x–x3)…(x – xn) + A1(x–x1)(x–x2)(x–x3)…(x – xn) + … + A(n-1)(x–x1)(x–x2)(x–x3)…(x – xn)

Aizstāj novērojumus xilai iegūtu Ai

Ielieciet x = x0tad mēs saņemam A0

operatori python programmēšanā

f(x0) = un0= A0(x0– x1)(x0– x2)(x0– x3)…(x0– xn)

A 0 = un 0 /(x 0 – x 1 )(x 0 – x 2 )(x 0 – x 3 )…(x 0 – x n )

Aizstājot x = x1mēs saņemam A1

f(x1) = un1= A1(x1– x0)(x1– x2)(x1– x3)…(x1– xn)

A 1 = un 1 /(x 1 – x 0 )(x 1 – x 2 )(x 1 – x 3 )…(x 1 – x n )

Līdzīgi, aizstājot x = xnmēs saņemam An

f(xn) = unn= An(xn– x0)(xn– x1)(xn– x2)…(xn– xn-1)

A n = un n /(x n – x 0 )(x n – x 1 )(x n – x 2 )…(x n – x n-1 )

Ja mēs aizstājam visas A vērtībasifunkcijā f(x), kur i = 1, 2, 3, …n, tad mēs iegūstam Lagranža interpolācijas formulu kā,

f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} reizes y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n

Lagranža interpolācijas formulas īpašības

Tālāk ir apskatītas dažādas Lagranža interpolācijas formulas īpašības,

  • Šo formulu izmanto, lai atrastu funkcijas vērtību jebkurā brīdī, pat ja pati funkcija nav dota.
  • To lieto pat tad, ja norādītie punkti nav vienmērīgi izvietoti.
  • Tas dod atkarīgā mainīgā vērtību jebkuram neatkarīgam mainīgajam, kas pieder jebkurai funkcijai, un tādējādi tiek izmantots skaitļu analīzē, lai atrastu funkcijas vērtības utt.

Lagranža interpolācijas formulas lietojumi

Tālāk ir apskatīti dažādi Lagranža interpolācijas formulas lietojumi,

  • To izmanto, lai atrastu atkarīgā mainīgā vērtību pie jebkura konkrēta neatkarīga mainīgā, pat ja pati funkcija nav dota.
  • To izmanto attēla mērogošanā.
  • To izmanto AI modelēšanā.
  • To izmanto, lai mācītu NLP utt.

Lasīt vairāk,

  • Interpolācijas formula
  • Lineārā interpolācijas formula

Lagranža interpolācijas formulas izmantošanas piemēri

Apskatīsim dažus jautājumu paraugus par Lagranža interpolācijas formulu.

1. piemērs: atrodiet y vērtību pie x = 2 dotajai punktu kopai (1, 2), (3, 4)

Risinājums:

Ņemot vērā,

  • (x0, un0) = (1, 2)
  • (x1, un1) = (3, 4)

Pirmās kārtas Lagranža interpolācijas formula ir,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Pie x = 2

un =~frac{(2-3)}{(1-3)} imes 2+frac{(2-1)}{(3-1)} imes 4

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

Y vērtība pie x = 2 ir 3

2. piemērs: atrodiet y vērtību pie x = 5 dotajai punktu kopai (9, 2), (3, 10)

Risinājums:

Ņemot vērā,

  • (x0, un0) = (9, 2)
  • (x1, un1) = (3, 10)

Pirmās kārtas Lagranža interpolācijas formula ir,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Pie x = 5

y~=~frac{(5-3)}{(9-3)} imes 2+frac{(5-9)}{(3-9)} imes 10

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

Y vērtība pie x = 5 ir 7,33

3. piemērs. Atrodiet y vērtību pie x = 1 dotajai punktu kopai (1, 6), (3, 4), (2, 5)

Risinājums:

Ņemot vērā,

  • (x0, un0) = (1, 6)
  • (x1, un1) = (3, 4)
  • (x2, un2) = (2, 5)

Otrās kārtas Lagranža interpolācijas formula ir,

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1) -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Pie x = 1

y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} imes 6+frac{(1-1)(1-2)}{( 3-1)(3-2)} eizes 4+frak{(1-1)(1-3)}{(2-1)(2-3)} eizes 5 y~=~ frac{(-2)(-1)}{(-2)(-1)} imes 6+frac{(0)(-1)}{(2)(1)} imes 4+frac {(0)(-2)}{(1)(-1)} imes 5

y = (12/2) + 0 + 0

y = 6

Y vērtība pie x = 1 ir 6

4. piemērs. Atrodiet y vērtību pie x = 10 dotajai punktu kopai (9, 6), (3, 5), (1, 12)

Risinājums:

Ņemot vērā,

  • (x0, un0) = (9, 6)
  • (x1, un1) = (3, 5)
  • (x2, un2) = (1, 12)

Otrās kārtas Lagranža interpolācijas formula ir,

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1) -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Pie x = 10

y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)} eizes 5+frak{(10-9)(10-3)}{(1-9)(1-3)} eizes 12 y~=~ frac{(7)(9)}{(6)(8)} imes 6+frac{(1)(9)}{(-6)(2)} imes 5+frac{(1) (7)}{(-8)(-2)} imes 12

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

Y vērtība pie x = 10 ir 9,375

5. piemērs. Atrodiet y vērtību pie x = 7 dotajai punktu kopai (1, 10), (2, 4), (3, 4), (5, 7)

Risinājums:

Ņemot vērā,

  • (x0, un0) = (1, 10)
  • (x1, un1) = (2, 4)
  • (x2, un2) = (3, 4)
  • (x3, un3) = (5, 7)

Trešās kārtas Lagranža interpolācijas formula ir,

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)} imes y_3

Pie x = 7

y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)} imes 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)} imes 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} imes 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)} eizes 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)} imes 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} imes 4+frac{(6)(5)(2)}{(2)(1) (-2)} eizes 4+frak{(6)(5)(4)}{(4)(3)(2)} eizes 7

y = -50 + 64 - 60 + 35

y = 99–110 = - vienpadsmit

Y vērtība pie x = 7 ir -11

6. piemērs. Atrodiet y vērtību pie x = 10 dotajai punktu kopai (5, 12), (6, 13), (7, 14), (8, 15).

Risinājums:

Ņemot vērā,

  • (x0, un0) = (5, 12)
  • (x1, un1) = (6, 13)
  • (x2, un2) = (7, 14)
  • (x3, un3) = (8, 15)

Trešās kārtas Lagranža interpolācijas formula ir,

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)} imes y_3

Ja x = 10,

y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)} imes 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)} imes 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)} imes 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)} imes 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)} imes 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} imes 13+frac{(5)(4)(2)}{(2)(1) (-1)} eizes 14+frak{(5)(4)(3)}{(3)(2)(1)} eizes 15

y = -48 + 195 - 280 + 150

y = 17

Y vērtība pie x = 10 ir 17

7. piemērs. Atrodiet y vērtību pie x = 0 dotajai punktu kopai (-2, 5), (1, 7)

Risinājums:

Ņemot vērā,

  • (x0, un0) = (-2, 5)
  • (x1, un1) = (1, 7)

Pirmās kārtas Lagranža interpolācijas formula ir,

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

pie x = 0,

y~=~frac{(0-1)}{(-2-1)} imes 5+frac{(0+2)}{(1+2)} imes 7

y = (5/3) + (14/3)

y = 19/3 = 6,33

Y vērtība pie x = 0 ir 6,33

FAQ par Lagranža interpolācijas formulu

1. Kas ir Lagranža interpolācijas formula?

Lagranža interpolācijas formula ir formula, ko izmanto, lai atrastu funkcijas atkarīgā mainīgā vērtību jebkuram neatkarīgam mainīgajam, pat ja pati funkcija nav norādīta.

2. Kādi ir Lagranža interpolācijas formulas pielietojumi?

Lagranges formulai ir dažādi pielietojumi mūsdienu matemātikā un datu zinātnēs,

  • Tas tiek izmantots AI modelim Traning.
  • To izmanto attēlu apstrādē.
  • To izmanto trīsdimensiju un augstāku līkņu attēlošanai utt.

3. Kas ir pirmās kārtas Lagranža interpolācijas formula?

Pirmās kārtas Lagranža interpolācijas formula ir,

f(x) = (x – x 1 )/(x 0 – x 1 )×f 0 + (x – x 0 )/(x 1 – x 0 )×f 1

4. Kas ir otrās kārtas Lagranža interpolācijas formula?

Otrās kārtas Lagranža interpolācijas formula ir,

f(x) = [(x – x 1 )(x–x 2 )/(x 0 – x 1 )(x 0 – x 2 )]×f 0 + [(x – x 0 )(x–x 2 )/(x 1 – x 0 )(x 1 – x 2 )]×f 1 + [(x – x 0 )(x–x 1 )/(x 2 – x 0 )(x 2 – x 2 )]×f 0