A Režisēts aciklisks grafiks , bieži saīsināti kā DIENA , ir grafu teorijas pamatjēdziens. DAG tiek izmantoti, lai skaidri un organizēti parādītu, kā lietas ir saistītas vai ir atkarīgas viena no otras. Šajā rakstā mēs uzzināsim par Režisēts aciklisks grafiks , tā īpašības un pielietojums reālajā dzīvē.

Režisēts aciklisks grafiks

Kas ir virzītais acikliskais grafiks?

A Režisēts aciklisks grafiks (DAG) ir virzīts grafiks, kas nesatur nevienu ciklu.

Zemāk redzamajā diagrammā ir attēlots virzīts aciklisks grafiks (DAG):

Tiešais acikliskais grafiks

Virzītā acikliskā grafika nozīme:

Režisētajam acikliskajam grafikam ir divas svarīgas funkcijas:

• Režisors Edžs s:virzītajā acikliskajā diagrammā, katrai malai ir virziens, kas nozīmē, ka tā iet no vienas virsotnes (mezgla) uz otru. Šis virziens apzīmē a vienvirziena attiecības vai atkarība starp mezgliem.
• Aciklisks: Termiņš aciklisks norāda, ka grafikā nav ciklu vai slēgtu cilpu. Citiem vārdiem sakot, jūs nevarat šķērsot virzītu malu secību un atgriezties tajā pašā mezglā, ievērojot malu virzienus. Ciklu veidošanās ir aizliegta DIENA. Tāpēc šī īpašība ir būtiska.

Režisēts aciklisks grafiks

Virzītā acikliskā grafika DAG īpašības:

Directed Acyclic Graph (DAG) ir dažādas īpašības, kas padara tos izmantojamus grafiku problēmās.

Ir šādas virzītās acikliskās diagrammas (DAG) īpašības:

• Sasniedzamības attiecība: Programmā DAG mēs varam noteikt, vai starp diviem mezgliem pastāv sasniedzamības attiecība. Tiek uzskatīts, ka mezgls A ir sasniedzams no mezgla B, ja pastāv virzīts ceļš, kas sākas mezglā B un beidzas mezglā A. Tas nozīmē, ka varat sekot diagrammas malu virzienam, lai nokļūtu no B uz A.
• Pārejas slēgšana: Virzīta grafika pārejoša slēgšana ir jauns grafiks, kas attēlo visas tiešās un netiešās attiecības vai savienojumus starp mezgliem sākotnējā diagrammā. Citiem vārdiem sakot, tas norāda, kurus mezglus var sasniegt no citiem mezgliem, sekojot vienai vai vairākām virzītām malām.

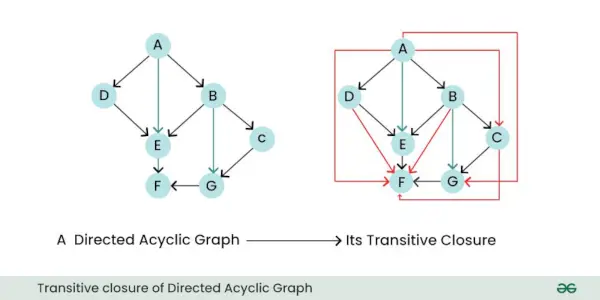
Virzīta acikliskā grafika pārejoša slēgšana

• Transitīvā samazināšana: Virzīta grafika pārejoša samazināšana ir jauns grafiks, kas saglabā tikai būtiskās, tiešās attiecības starp mezgliem, vienlaikus noņemot visas nevajadzīgās netiešās malas. Būtībā tas vienkāršo grafiku, novēršot malas, kuras var secināt no atlikušajām malām.

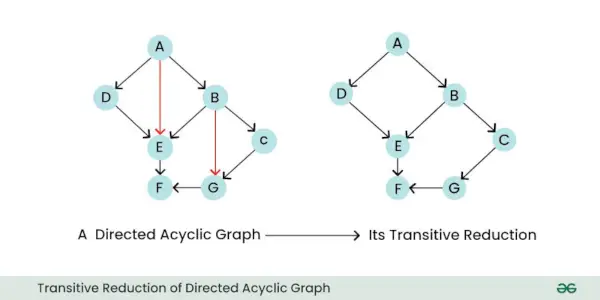
Virzīta acikliskā grafika pārejoša samazināšana

• Topoloģiskā secība: DAG var kārtot topoloģiski, kas nozīmē, ka varat lineāri sakārtot tā mezglus tā, lai visām malām malas sākuma mezgls atrastos agrāk secībā. Šis rekvizīts ir noderīgs tādiem uzdevumiem kā plānošana un atkarības atrisināšana.

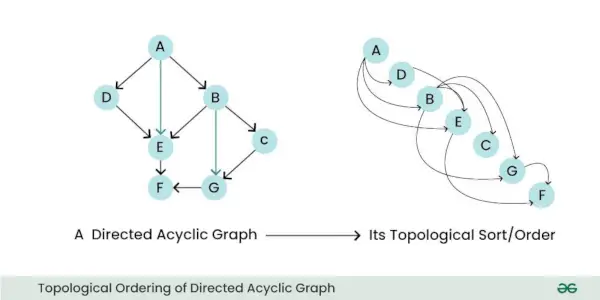
Virzīto aciklisko grafiku topoloģiskā secība

DAG praktiskie pielietojumi:

• Datu plūsmas analīze: Kompilatoru projektēšanā un optimizācijā DAG izmanto, lai attēlotu datu plūsmu programmā. Tas palīdz optimizēt kodu, identificējot liekos aprēķinus un mirušo kodu. DAG izmanto arī, lai attēlotu struktūru pamata bloki sadaļā Kompilatoru dizains.

• Uzdevumu plānošana: DAG tiek izmantoti projektu vadībā un darbu plānošanā. Katrs uzdevums vai darbs tiek attēlots kā mezgls DAG ar novirzītām malām, kas norāda uz atkarībām. DAG acikliskais raksturs nodrošina, ka uzdevumi tiek ieplānoti loģiskā secībā, novēršot cirkulāras atkarības.

Svērtu virzītu aciklisku grafiku var izmantot, lai attēlotu plānošanas problēmu. Ņemsim piemēru par uzdevumu plānošanas problēmu. Šeit virsotne var attēlot uzdevumu, un tās svars var attēlot uzdevuma aprēķina lielumu. Līdzīgi mala var attēlot saziņu starp diviem uzdevumiem, un tās svars var atspoguļot komunikācijas izmaksas:

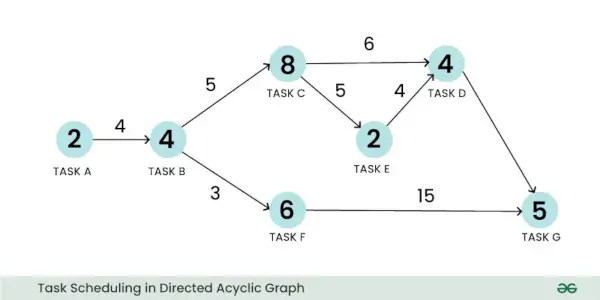
Uzdevumu plānošana virzītā acikliskā diagrammā

Secinājums:

Rezumējot, virzīti acikliskie grafiki ir grafu teorijas pamatjēdziens ar daudziem praktiskiem pielietojumiem. DAG ir izšķiroša loma uzdevumu plānošanā, datu plūsmas analīzē, atkarības izšķiršanā un dažādās citās datorzinātņu un inženierijas jomās. Tie palīdz optimizēt procesus, pārvaldīt atkarības un nodrošināt efektīvu uzdevumu vai darbu izpildi.