Trīsstūra centrējums ir visu trīs trijstūra leņķa bisektrišu krustpunkts. Incents ir svarīgs punkts trijstūrī, kur savienojas līnijas, kas sagriež leņķus uz pusēm. Šis punkts ir arī apļa centrs ar nosaukumu Incircle, kas lieliski iederas trijstūra iekšpusē un vienādi pieskaras visām trim malām. Šajā rakstā ir aplūkoti dažādi trijstūra centra jēdzieni, piemēram, kāpēc šis punkts ir svarīgs, kā to atrast, izmantojot kompasu vai skaitļus, un apļa centra īpašības.

Satura rādītājs

• Kas ir trijstūra incents?
• Trijstūra incenta īpašības
• Trīsstūra formulas centrējums
• Kā atrast trīsstūra centrējumu
• Centroid, Circumcenter, Incenter, Orthocenter

Kas ir trijstūra incents?

Trijstūra viduspunkts, kā norāda nosaukums, ir trijstūra centra punkts. Šis punkts, ko mēs saucam par centrējumu, veidojas krustojumā, kur satiekas visas līnijas, kas sadala iekšējos leņķus. Punkta attālums no visām trim trijstūra malām ir vienāds. Trijstūra aplis arī iederas perfektā aplī trijstūra iekšpusē, un šo apli sauc par trijstūra apli.

Incenta definīcija

Trijstūra viduspunkts ir punkts trīsstūra iekšpusē, kur visas trīs līnijas, kas sagriež tā iekšējos leņķus uz pusēm, saplūst. Šis punkts atrodas tādā pašā attālumā no trijstūra trim malām, padarot to līdzīgu trijstūra vidum. Tas ir arī lielākā apļa centrs, kas var cieši ietilpt trīsstūrī, ko mēs saucam par apli. Lai simbolizētu centru, mēs parasti lietojam burtu I,

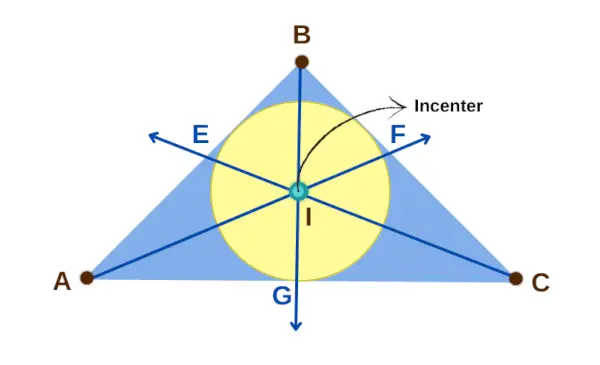
Trīsstūra centrējums

Trijstūra incenta īpašības

Tālāk ir norādītas dažas svarīgas trīsstūra centra īpašības:

1. īpašums: Ja es ir trijstūra ABC centrs, tad trīs līniju segmentu pāri ir vienādi garumā: AE un AG, CG un CF, un BF un BE. Tas nozīmē, ka AE = AG, CG = CF un BF = BE.

2. īpašums: Centrs es ir arī īpašas attiecības ar trijstūra leņķiem. Tā rezultātā leņķi ∠BAI un ∠CAI ir vienādi, ∠BCI un ∠ACI ir vienādi un ∠ABI un ∠CBI ir vienādi. Tas seko leņķa bisektrise teorēmai.

3. īpašums: Centrs es ir apļa centrs, kas skar visas trīs trijstūra malas, un attālumi no es trijstūra malām (EI, FI, GI) ir vienādas. Šos attālumus sauc par inradii vai apļa rādiusu.

4. īpašums: Trijstūra laukumu var aprēķināt, izmantojot pusperimetru (s) un rādiusu (r). Formula ir A = sr, kur A ir laukums, s ir pusperimetrs (s = (a + b + c)/2, kur a, b un c ir trijstūra malu garumi), un r ir rādiuss.

5. īpašums: Trijstūra viduspunkts vienmēr paliek trīsstūra iekšpusē. Atšķirībā no ortocentra, kas dažos gadījumos var būt ārpus trijstūra, centrējums vienmēr atrodas trīsstūra robežās.

Trīsstūra formulas centrējums

Formula, lai atrastu formulas centru ar 3 koordinātām (x₁, un₁), (x₂, un₂), un (x₃, un₃) ir:

{(cirvis ₁ + bx ₂ + cx ₃ )/(a + b + c), (ir ₁ + autors ₂ + c ₃ )/(a + b + c)}

Vienkārši sakot, lai iegūtu centru, jums:

• Reiziniet punkta A x koordinātu ar malas garumu a, punkta B x koordinātu ar malas garumu b un punkta C x koordinātu ar malas garumu c. Pēc tam pievienojiet tos kopā.
• Sadaliet rezultātu ar malu garumu a, b un c summu.
• Atkārtojiet to pašu procesu ar y koordinātām, bet izmantojot malu garumus a, b un c.

Trīsstūra leņķa formulas iecentrs

Formula trijstūra leņķa centra atrašanai ir šāda:

Pieņemsim, ka trijstūrī D, F un G ir punkti, kur attiecīgi leņķu A, B un C leņķa bisektrise saskaras ar malām BC, AC un AB.

Leņķi ∠AIB (kur I ir trijstūra viduspunkts) var aprēķināt, izmantojot formulu:

∠AIB = 180° – (puse no leņķu A un B summas)

VAI

∠AIB = 180° – (∠A + ∠B)/2

Kā atrast trīsstūra centrējumu

Trīsstūra centra atrašanai ir divas metodes. Būvniecībā mēs atrodam centrējumu, zīmējot trijstūra leņķa bisektrise. Koordinātu ģeometrijā mēs izmantojam formulu, lai noteiktu incentu.

Koordinātu ģeometrijas izmantošana : atrodiet trijstūra centru ar koordinātām, kas norādītas kā: A(2, 2), B(6, 2) un C(4, 5)

Saskaņā ar sniegto informāciju

• (x₁, un₁) = (2, 2)
• (x₂, un₂) = (6, 2)
• (x₃, un₃) = (4, 5)

Mēs zinām, ka trijstūra centrs ir:

I(x, y) = {(cirvis ₁ + bx ₂ + cx ₃ )/(a + b + c), (ir ₁ + autors ₂ + c ₃ )/(a + b + c)}

A malai: attālums starp punktiem B un C = √((6–4)²+ (2–5)²) = √8

Malai b: attālums starp punktiem A un C = √((2–4)²+ (2–5)²) = √13

C malai: attālums starp punktiem A un B = √((6–2)²+ (2–2)²) = 4

Ievietojot a, b, c vērtības incenta formulā, mēs iegūstam:

I(x, y) = {(8 × 2 + 13 × 5 + 4 × 4)/(8 + 13 +4), (8 × 2 + 13 × 2 + 4 × 5) / (8 + 13 +4 )}

⇒ I(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)

⇒ I(x, y) = (110/25, 62/25) = (22/5,62/25)

∴ Trijstūra ABC centrs ar koordinātām ir (22/5,62/25)

Kā izveidot trijstūra centrējumu?

Lai izveidotu trijstūra centru, būs jāizmanto kompass. Izmantojot kompasu, veiciet tālāk norādītās darbības.

1. darbība: Novietojiet vienu kompasa galu uz trijstūra virsotnes, un otrs gals pieskaras vienai malai.

2. darbība: Izmantojiet kompasu, lai uzzīmētu divus lokus abās trīsstūra malās.

3. darbība: Ar tādu pašu attālumu uz kompasa izveidojiet divus lokus trīsstūra iekšpusē. Šiem lokiem vajadzētu šķērsot viens otru no vietas, kur tie pieskaras malām.

4. darbība: Novelciet līniju no trīsstūra virsotnes līdz vietai, kur krustojas divi iekšējie loki.

5. darbība: Atkārtojiet tās pašas darbības no otras trīsstūra virsotnes.

6. darbība: Vieta, kur abas līnijas saskaras vai krustojas, ir trijstūra viduspunkts.

Taisnleņķa trijstūra centrējums

Centrs, ja a Taisnleņķa trīsstūris ir punkts, kur satiekas visas taisnleņķa trijstūra leņķa bisektrise. Ja taisnleņķa trijstūra malas mēra a, b un c, tad apļa “r” rādiuss tiek dots kā r = (ab)/(a + b + c). Labā trīsstūra vidusdaļa ir parādīta zemāk:

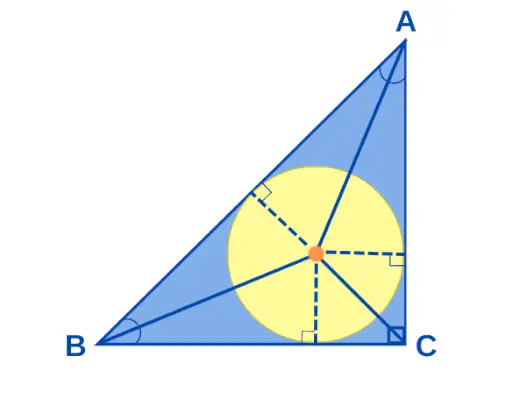
Taisnleņķa trijstūra centrējums

Centroid, Circumcenter, Incenter, Orthocenter

Centroid, Circumcenter, Incenter un Orthocenter ir četri svarīgi punkti, kas saistīti ar traingle. Salīdzinājums starp Centroid, Circumcenter, Incenter un Orthocenter ir parādīts tabulā zemāk:

Tāpat pārbaudiet

• Trīsstūra laukums
• Trijstūra perimetrs
• Trijstūra leņķa summas īpašība

Trijstūra centrējuma piemēri

1. piemērs: Aprēķiniet trijstūra ABC centrējumu. AB= 8cm, BC= 15 cm, CA= 17 cm.

Risinājums:

Izmantojot formulu Trijstūra incents = (aA + bB + cC)/(a + b + c)

kur,

• a = 8
• b = 15
• c = 17

Un leņķi ir,

• A = 30°
• B = 60°
• C = 90°

Ievietojot šīs vērtības formulā, lai iegūtu,

⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}

⇒ (240 + 900 + 1530)/40

⇒ 2670/40

⇒ 66,75

2. piemērs: Džeina aprēķināja trīsstūrveida lauka laukumu kā 120 kvadrātmetrus. Lauka perimetrs ir 36 metri. Ja trijstūra iekšpusē ir ievilkts aplis tā, ka tas skar katru trijstūra malu, palīdziet Džeinai aprēķināt trijstūra rādiusu.

Risinājums:

Saskaņā ar sniegto informāciju,

Trijstūra laukums = 120 kvadrātmetri

Trijstūra perimetrs = 36 metri

Mēs zinām, ka trijstūra laukums = r × s

s = pusperimetrs

s = p/2 = 36/2 = 18

A = r × s

r = A/s

r = 120/18

r = 6,67 metri

imessage spēles Android ierīcēs

Prakses uzdevumi trijstūra centrēšanai

1. uzdevums: dots trīsstūris PQR ar virsotnēm P(1, 2), Q(4, 6) un R(7, 2), atrodiet centra koordinātas.

2. uzdevums: izveidojiet trīsstūri ABC ar ∠A = 45°, ∠B = 60° un ∠C = 75°. Izmantojiet konstrukcijas metodi, lai atrastu centru.

3. uzdevums: trijstūrī LMN, ja ∠L = 75°, ∠M = 60° un ∠N = 45°, atrodiet centra koordinātas.

4. uzdevums: izveidojiet trīsstūri XYZ ar ∠X = 80°, ∠Y = 50° un ∠Z = 50°. Izmantojiet konstrukcijas metodi, lai atrastu centru.

Trīsstūra centrējums: FAQ

Kas ir trijstūra incents?

Trijstūra viduspunkts ir punkts, kurā krustojas iekšējo leņķu bisektrise. Tas atrodas vienādā attālumā no visām trim trijstūra malām.

Kāda ir centrējuma nozīme trīsstūrī?

Incents ir nozīmīgs, jo tas ir trijstūra apļa centrs, lielākais aplis, kas iekļaujas trīsstūra iekšpusē. Tam ir īpašība būt vienādā attālumā no visām pusēm.

Vai incents var būt ārpus trīsstūra?

Nē, centrs vienmēr atrodas trīsstūra iekšpusē. Tas ir leņķa bisektoru sakritības punkts, un pēc definīcijas tam jāatrodas trīsstūra robežās.

Kā tiek izveidots incents, izmantojot kompasu un taisno malu?

Lai izveidotu centrējumu, izmantojiet kompasu, lai no katras virsotnes uz pretējo pusi novilktu leņķa bisektrise. Incents ir punkts, kur šīs bisektrise krustojas.

Kas ir Incenter Formula?

Trijstūra incenta formulu var uzrakstīt šādi:

frac{(aA+bB+cC)}{a+b+c}

Kādas ir trīsstūra centra īpašības?

Centram ir dažas galvenās īpašības. Tas atrodas vienādā attālumā no trijstūra malām, kas nozīmē, ka attālumi līdz malām ir vienādi. Tas ir arī leņķa bisektoru krustpunkts, sadalot leņķus divās vienādās daļās.

Kā tiek noteikts centrs?

Lai noteiktu incentu, jāatrod vieta, kur krustojas leņķa bisektrise. To var izdarīt, izmantojot centrēšanas formulu vai zīmējot leņķa bisektorus un atrodot to krustpunktu.

Kāda ir atšķirība starp Incentre un Circumcentre?

Galvenā atšķirība starp incenter un circumcenter ir to fokuss. Incenter attiecas uz leņķa bisektriecēm un ir ierakstītā apļa centrs, savukārt apkārtmēra centrs attiecas uz perpendikulārām bisektriecēm un ir ierobežotā apļa centrs.

Vai Incentre un Centroid ir vienādi?

Nē, centrs un centrs atšķiras. Centrs ir vieta, kur satiekas leņķa bisektrise, turpretim centroīds ir vieta, kur krustojas mediānas. Mediānas savieno virsotnes ar pretējās puses viduspunktu.

Vai Incentrs un Ortocentrs ir viens un tas pats?

Nē, centrs un ortocentrs nav viens un tas pats. Centrs ir punkts, kur leņķis sadala viens otru, savukārt ortocentrs ietver augstumus - līnijas no katras virsotnes, kas ir perpendikulāra pretējai pusei. Tie ir dažādi punkti trīsstūrī.