• Kalnā kāpšanas algoritms ir lokāls meklēšanas algoritms, kas nepārtraukti pārvietojas augstuma/vērtības pieauguma virzienā, lai atrastu kalna virsotni vai labāko problēmas risinājumu. Tas beidzas, kad tas sasniedz maksimālo vērtību, kur nevienam kaimiņam nav lielākas vērtības.
• Kalnā kāpšanas algoritms ir paņēmiens, ko izmanto matemātisko problēmu optimizēšanai. Viens no plaši apspriestajiem kalnā kāpšanas algoritma piemēriem ir Travelling-salesman Problem, kurā mums ir jāsamazina pārdevēja nobrauktais attālums.
• To sauc arī par mantkārīgu vietējo meklēšanu, jo tā skatās tikai uz savu labo tuvāko kaimiņvalsti, nevis tālāk.
• Kalnā kāpšanas algoritma mezglam ir divas sastāvdaļas, kas ir stāvoklis un vērtība.
• Kalnu kāpšana galvenokārt tiek izmantota, ja ir pieejama laba heiristika.
• Izmantojot šo algoritmu, mums nav jāuztur un jāapstrādā meklēšanas koks vai grafiks, jo tas saglabā tikai vienu pašreizējo stāvokli.

Kalnā kāpšanas iezīmes:

Tālāk ir norādītas dažas galvenās kalnā kāpšanas algoritma iezīmes:

Ģenerēt un pārbaudīt variantu:Kalnā kāpšana ir ģenerēšanas un pārbaudes metodes variants. Ģenerēšanas un pārbaudes metode rada atgriezenisko saiti, kas palīdz izlemt, kurā virzienā pārvietoties meklēšanas telpā.Mantkārīga pieeja:Kalnā kāpšanas algoritma meklēšana virzās virzienā, kas optimizē izmaksas.Nav atkāpšanās:Tas neatkāpjas no meklēšanas vietas, jo neatceras iepriekšējos stāvokļus.

Stāvokļa telpas diagramma kalnā kāpšanai:

Stāvokļa telpas ainava ir kalnā kāpšanas algoritma grafisks attēlojums, kas parāda grafiku starp dažādiem algoritma stāvokļiem un mērķa funkciju/izmaksu.

Uz Y ass esam izvēlējušies funkciju, kas var būt mērķa funkcija vai izmaksu funkcija, un stāvokļa telpa uz x ass. Ja Y ass funkcija ir maksa, meklēšanas mērķis ir atrast globālo minimumu un lokālo minimumu. Ja Y ass funkcija ir Objective funkcija, tad meklēšanas mērķis ir atrast globālo maksimumu un lokālo maksimumu.

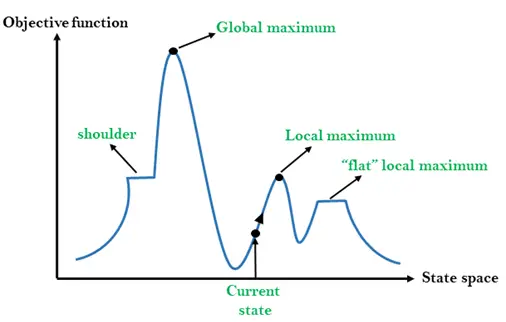
Dažādi reģioni valsts telpas ainavā:

Vietējais maksimums: Vietējais maksimums ir stāvoklis, kas ir labāks par kaimiņvalstīm, taču ir arī cits stāvoklis, kas ir augstāks par to.

Globālais maksimums: Globālais maksimums ir labākais iespējamais valsts telpas ainavas stāvoklis. Tam ir visaugstākā mērķa funkcijas vērtība.

Pašreizējais stāvoklis: Tas ir stāvoklis ainavas diagrammā, kurā pašlaik atrodas aģents.

Plakans vietējais maksimums: Tā ir līdzena telpa ainavā, kurā visiem pašreizējo štatu kaimiņvalstīm ir vienāda vērtība.

jauna līnija python

Plecs: Tas ir plato reģions, kuram ir kalna mala.

Kalnā kāpšanas algoritmu veidi:

• Vienkārša kāpšana kalnā:
• Stāvākais kāpums kalnā:
• Stohastiskā kāpšana kalnā:

1. Vienkārša kāpšana kalnā:

Vienkārša kāpšana kalnā ir vienkāršākais veids, kā ieviest kalnā kāpšanas algoritmu. Tas vienlaikus novērtē tikai kaimiņu mezgla stāvokli un atlasa pirmo, kas optimizē pašreizējās izmaksas un iestata to kā pašreizējo stāvokli. . Tas tikai pārbauda, ​​vai tas ir viens pēctecis, un, ja tiek atrasts labāks par pašreizējo stāvokli, pārvietojiet citur, lai būtu tajā pašā stāvoklī. Šim algoritmam ir šādas funkcijas:

• Mazāk laikietilpīga
• Mazāk optimāls risinājums un risinājums netiek garantēts

Algoritms vienkāršai kāpšanai kalnā:

1. darbība:Novērtējiet sākotnējo stāvokli, ja tas ir mērķa stāvoklis, atgriezieties panākumos un Stop.2. darbība:Cikls Līdz tiek atrasts risinājums vai nav atlicis neviens jauns operators, kuram pieteikties.3. darbība:Izvēlieties un lietojiet operatoru pašreizējam stāvoklim.4. darbība:Pārbaudiet jauno stāvokli:
1. Ja tas ir mērķa stāvoklis, atdodiet panākumus un pametiet.
2. Ja tas ir labāks par pašreizējo stāvokli, piešķiriet jaunu stāvokli kā pašreizējo stāvokli.
3. Ja ne labāk par pašreizējo stāvokli, atgriezieties pie 2. darbības.
5. darbība:Izeja.

2. Stāvākais kāpums kalnā:

Stāvākā pacelšanās algoritms ir vienkārša kalnā kāpšanas algoritma variācija. Šis algoritms pārbauda visus pašreizējā stāvokļa blakus mezglus un atlasa vienu kaimiņu mezglu, kas ir vistuvāk mērķa stāvoklim. Šis algoritms patērē vairāk laika, jo tiek meklēti vairāki kaimiņi

Algoritms kāpšanai kalnā stāvākajam kāpumam:

1. darbība:Novērtējiet sākotnējo stāvokli, ja tas ir mērķa stāvoklis, atdodiet panākumus un apstājieties, pretējā gadījumā izveidojiet pašreizējo stāvokli kā sākotnējo stāvokli.2. darbība:Veiciet cilpu, līdz tiek atrasts risinājums vai pašreizējais stāvoklis nemainās.
1. Lai SUCC ir tāds stāvoklis, ka jebkurš pašreizējā stāvokļa pēctecis būs labāks par to.
2. Katram operatoram, kas attiecas uz pašreizējo stāvokli:
   1. Lietojiet jauno operatoru un ģenerējiet jaunu stāvokli.
   2. Novērtējiet jauno stāvokli.
   3. Ja tas ir mērķa stāvoklis, atgrieziet to un pametiet, pretējā gadījumā salīdziniet to ar SUCC.
   4. Ja tas ir labāks par SUCC, iestatiet jauno stāvokli kā SUCC.
   5. Ja SUCC ir labāks par pašreizējo stāvokli, iestatiet pašreizējo stāvokli uz SUCC.
5. darbība:Izeja.

3. Stohastiskā kāpšana kalnā:

Stohastiskā kāpšana kalnā pirms pārcelšanās nepārbauda visus kaimiņus. Drīzāk šis meklēšanas algoritms nejauši atlasa vienu kaimiņu mezglu un izlemj, vai izvēlēties to kā pašreizējo stāvokli vai pārbaudīt citu stāvokli.

Problēmas kalnā kāpšanas algoritmā:

1. Lokālais maksimums: Lokālais maksimums ir pīķa stāvoklis ainavā, kas ir labāks par katru no blakus esošajiem stāvokļiem, taču ir arī cits stāvoklis, kas ir augstāks par vietējo maksimumu.

Risinājums: Atkāpšanās tehnika var būt lokālā maksimuma risinājums valsts telpas ainavā. Izveidojiet daudzsološā ceļa sarakstu, lai algoritms varētu atgriezties meklēšanas telpā un izpētīt arī citus ceļus.

2. Plato: Plato ir meklēšanas telpas plakana zona, kurā visi pašreizējā stāvokļa kaimiņu stāvokļi satur vienu un to pašu vērtību, jo šis algoritms neatrod labāko virzienu kustībai. Meklēšana kalnā var tikt zaudēta plato apgabalā.

Risinājums: Plato risinājums ir spert lielus vai ļoti mazus soļus, meklējot, lai atrisinātu problēmu. Nejauši atlasiet stāvokli, kas atrodas tālu no pašreizējā stāvokļa, tāpēc ir iespējams, ka algoritms varētu atrast reģionu, kas nav plato.

3. Izciļņi: Ridge ir īpaša vietējā maksimuma forma. Tam ir platība, kas ir augstāka par apkārtējām teritorijām, bet tai ir slīpums, un to nevar sasniegt ar vienu kustību.

Risinājums: Izmantojot divvirzienu meklēšanu vai pārvietojoties dažādos virzienos, mēs varam uzlabot šo problēmu.

Simulētā atkausēšana:

Kalnā kāpšanas algoritms, kas nekad nepārvietojas uz zemāku vērtību, garantēts, ka tas ir nepilnīgs, jo tas var iestrēgt vietējā maksimumā. Un, ja algoritms izmanto nejaušu gājienu, pārvietojot pēcteci, tas var pabeigt, bet neefektīvi. Simulētā atkvēlināšana ir algoritms, kas nodrošina gan efektivitāti, gan pilnīgumu.

Mehāniskā ziņā Atkausēšana ir metāla vai stikla sacietēšanas process līdz augstai temperatūrai, pēc tam pakāpeniski atdzesējot, tādējādi ļaujot metālam sasniegt zemas enerģijas kristālisko stāvokli. Tas pats process tiek izmantots simulētajā rūdīšanā, kurā algoritms izvēlas nejaušu kustību, nevis labāko kustību. Ja nejaušā kustība uzlabo stāvokli, tad tā iet to pašu ceļu. Pretējā gadījumā algoritms iet pa ceļu, kura varbūtība ir mazāka par 1, vai arī virzās lejup un izvēlas citu ceļu.