Hierarhiskā klasterizācija attiecas uz nepārraudzītu mācību procedūru, kas nosaka secīgus klasterus, pamatojoties uz iepriekš definētiem klasteriem. Tas darbojas, grupējot datus klasteru kokā. Hierarhiskā klasterizācijas statistika, katru datu punktu apstrādājot kā atsevišķu kopu. Galapunkts attiecas uz atšķirīgu klasteru kopu, kur katrs klasteris atšķiras no otras kopas, un objekti katrā klasterī ir tādi paši kā cits.

Ir divu veidu hierarhiskās klasterizācijas

• Aglomeratīvā hierarhiskā klasterizācija
• Sadalošā klasterizācija

Aglomeratīvā hierarhiskā klasterizācija

Aglomeratīvā klasterizācija ir viens no visizplatītākajiem hierarhiskās klasterizācijas veidiem, ko izmanto līdzīgu objektu grupēšanai klasteros. Aglomeratīvā klasterizācija ir pazīstama arī kā AGNES (aglomeratīvā ligzdošana). Aglomeratīvajā klasterizācijā katrs datu punkts darbojas kā atsevišķs klasteris, un katrā solī datu objekti tiek grupēti, izmantojot augšupēju metodi. Sākotnēji katrs datu objekts atrodas savā klasterī. Katrā iterācijā klasteri tiek apvienoti ar dažādām kopām, līdz tiek izveidots viens klasteris.

tīģera lauvas atšķirība

Aglomeratīvās hierarhiskās klasterizācijas algoritms

1. Nosakiet līdzību starp indivīdiem un visām pārējām kopām. (Atrast tuvuma matricu).
2. Apsveriet katru datu punktu kā atsevišķu kopu.
3. Apvienojiet līdzīgas kopas.
4. Pārrēķiniet katra klastera tuvuma matricu.
5. Atkārtojiet 3. un 4. darbību, līdz iegūstat vienu kopu.

Izpratīsim šo jēdzienu ar grafiskā attēlojuma palīdzību, izmantojot dendrogrammu.

Ar dotās demonstrācijas palīdzību mēs varam saprast, kā darbojas faktiskais algoritms. Šeit neviens aprēķins nav veikts, ja tiek pieņemts, ka ir tuvu klasteriem.

Pieņemsim, ka mums ir seši dažādi datu punkti P, Q, R, S, T, V.

šķirošanas tuples python

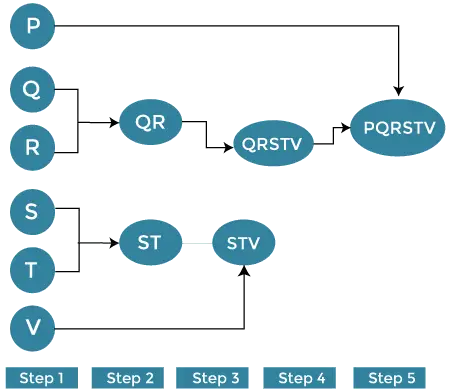
1. darbība:

Apsveriet katru alfabētu (P, Q, R, S, T, V) kā atsevišķu kopu un atrodiet attālumu starp atsevišķo klasteru no visām pārējām kopām.

skaitļi alfabētam

2. darbība:

Tagad apvienojiet salīdzināmās kopas vienā klasterī. Pieņemsim, ka klasteris Q un klasteris R ir līdzīgi viens otram, lai mēs varētu tos apvienot otrajā darbībā. Visbeidzot, mēs iegūstam kopas [ (P), (QR), (ST), (V)]

3. darbība:

Šeit mēs pārrēķinām tuvumu saskaņā ar algoritmu un apvienojam divus tuvākos klasterus [(ST), (V)] kopā, lai izveidotu jaunas kopas kā [(P), (QR), (STV)]

4. darbība:

Atkārtojiet to pašu procesu. STV un PQ klasteri ir salīdzināmi un apvienoti kopā, veidojot jaunu kopu. Tagad mums ir [(P), (QQRSTV)].

5. darbība:

pārvēršot virkni datumā

Visbeidzot, atlikušās divas kopas tiek apvienotas, lai izveidotu vienu kopu [(PQRSTV)]

Sadalošā hierarhiskā klasterizācija

Sadalošā hierarhiskā klasterizācija ir tieši pretēja aglomeratīvajai hierarhiskajai klasterizācijai. Sadalošajā hierarhiskajā klasterizācijā visi datu punkti tiek uzskatīti par atsevišķu kopu, un katrā iterācijā datu punkti, kas nav līdzīgi, tiek atdalīti no kopas. Atdalītie datu punkti tiek uzskatīti par atsevišķu kopu. Visbeidzot, mums paliek N kopas.

Hierarhiskās klasterizācijas priekšrocības

• Tas ir vienkārši īstenojams un dažos gadījumos nodrošina vislabāko rezultātu.
• Tas ir vienkārši un rada hierarhiju, struktūru, kas satur vairāk informācijas.
• Mums nav iepriekš jānorāda klasteru skaits.

Hierarhiskās klasterizācijas trūkumi

• Tas sadala lielās kopas.
• Ir grūti rīkoties ar dažāda izmēra klasteriem un izliektām formām.
• Tas ir jutīgs pret troksni un novirzēm.
• Algoritmu nekad nevar mainīt vai dzēst, ja tas ir izdarīts iepriekš.