Mantkārīgā metode ir viena no stratēģijām, piemēram, sadali un iekaro, ko izmanto problēmu risināšanai. Šo metodi izmanto optimizācijas problēmu risināšanai. Optimizācijas problēma ir problēma, kas prasa maksimālu vai minimālu rezultātu. Izpratīsim, izmantojot dažus terminus.
Mantkārīgā metode ir vienkāršākā un vienkāršākā pieeja. Tas nav algoritms, bet tā ir tehnika. Šīs pieejas galvenā funkcija ir lēmumu pieņemšana, pamatojoties uz pašlaik pieejamo informāciju. Neatkarīgi no pašreizējās informācijas, lēmums tiek pieņemts, neuztraucoties par pašreizējā lēmuma ietekmi nākotnē.
aritmētiskā loģiskā vienība
Šo paņēmienu pamatā izmanto, lai noteiktu iespējamo risinājumu, kas var būt vai nebūt optimāls. Iespējamais risinājums ir apakškopa, kas atbilst dotajiem kritērijiem. Optimālais risinājums ir risinājums, kas ir labākais un vislabvēlīgākais risinājums apakškopā. Iespējamā gadījumā, ja dotajiem kritērijiem atbilst vairāk nekā viens risinājums, tie tiks uzskatīti par iespējamiem, savukārt optimālais risinājums ir labākais risinājums no visiem risinājumiem.
Greedy metodes raksturojums
Tālāk ir norādītas mantkārīgas metodes pazīmes:
- Lai optimāli izveidotu risinājumu, šis algoritms izveido divas kopas, kur vienā komplektā ir visi izvēlētie vienumi, bet citā kopā ir noraidītie vienumi.
- Mantkārīgs algoritms veic labas vietējās izvēles, cerot, ka risinājumam jābūt vai nu īstenojamam, vai optimālam.
Mantkārīgā algoritma sastāvdaļas
Mantkārīgajā algoritmā var izmantot šādas sastāvdaļas:
pārveidotāja virkne līdz šim
Mantkārīgā algoritma pielietojumi
- To izmanto, lai atrastu īsāko ceļu.
- To izmanto, lai atrastu minimālo aptverošo koku, izmantojot prim algoritmu vai Kruskal algoritmu.
- To izmanto darbu secībā ar termiņu.
- Šis algoritms tiek izmantots arī daļējas mugursomas problēmas risināšanai.
Greedy Algorithm pseido kods
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } Iepriekš minētais ir mantkārīgais algoritms. Sākotnēji risinājumam tiek piešķirta nulles vērtība. Mēs nododam masīvu un elementu skaitu mantkārīgajā algoritmā. For cilpas iekšpusē mēs izvēlamies elementu pa vienam un pārbaudām, vai risinājums ir iespējams. Ja risinājums ir iespējams, mēs veicam savienību.
Sapratīsim, izmantojot piemēru.
Pieņemsim, ka ir problēma “P”. Es vēlos ceļot no A uz B, kā parādīts zemāk:
P : A → B
Problēma ir tāda, ka mums ir jādodas šajā ceļojumā no A līdz punktam B. Ir dažādi risinājumi, kā nokļūt no A līdz B. Mēs varam doties no A līdz B līdz plkst. pastaiga, mašīna, velosipēds, vilciens, lidmašīna u.c. Braucienam ir noteikts ierobežojums, ka mums šis brauciens ir jāveic 12 stundu laikā. Ja es braucu ar vilcienu vai lidmašīnu, es varu veikt šo attālumu 12 stundu laikā. Šai problēmai ir daudz risinājumu, taču ir tikai divi risinājumi, kas apmierina ierobežojumu.
klēpjdatora ievietošanas atslēga
Ja sakām, ka brauciens jāsedz ar minimālām izmaksām. Tas nozīmē, ka mums ir jānobrauc šis attālums pēc iespējas mazāks, tāpēc šī problēma ir pazīstama kā minimizēšanas problēma. Līdz šim mums ir divi iespējami risinājumi, t.i., viens ar vilcienu un otrs ar gaisa transportu. Tā kā ceļošana ar vilcienu radīs minimālas izmaksas, tāpēc tas ir optimāls risinājums. Optimāls risinājums ir arī iespējamais risinājums, bet nodrošinot vislabāko rezultātu, lai risinājums būtu optimālais risinājums ar minimālām izmaksām. Būtu tikai viens optimālais risinājums.
Problēmu, kas prasa minimālu vai maksimālo rezultātu, sauc par optimizācijas problēmu. Mantkārīgā metode ir viena no stratēģijām, ko izmanto optimizācijas problēmu risināšanai.
Greedy algoritma izmantošanas trūkumi
Mantkārīgs algoritms pieņem lēmumus, pamatojoties uz katrā fāzē pieejamo informāciju, neņemot vērā plašāku problēmu. Tāpēc var būt iespēja, ka mantkārīgais risinājums nesniedz labāko risinājumu katrai problēmai.
romiešu ciparu diagramma 1100
Tas katrā posmā seko vietējai optimālajai izvēlei, lai atrastu globālo optimālo. Sapratīsim, izmantojot piemēru.
Apsveriet diagrammu, kas parādīta zemāk:
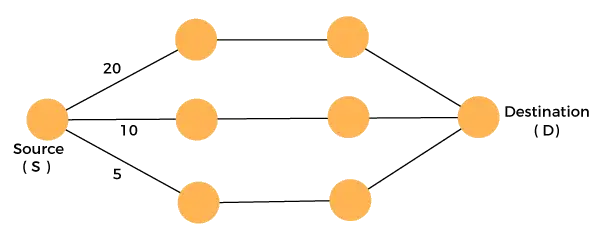
Mums ir jābrauc no avota līdz galamērķim ar minimālām izmaksām. Tā kā mums ir trīs iespējami risinājumi, kuru izmaksu ceļi ir 10, 20 un 5, 5 ir minimālo izmaksu ceļš, tāpēc tas ir optimālais risinājums. Tas ir lokālais optimums, un šādā veidā mēs atrodam lokālo optimumu katrā posmā, lai aprēķinātu globālo optimālo risinājumu.
