- Ierobežotā stāvokļa mašīna tiek izmantota, lai atpazītu modeļus.
- Ierobežots automāts izmanto simbola virkni kā ievadi un attiecīgi maina tā stāvokli. Ievadē, kad tiek atrasts vēlamais simbols, notiek pāreja.
- Pārejas laikā automāti var pāriet uz nākamo stāvokli vai palikt tajā pašā stāvoklī.
- FA ir divi stāvokļi: pieņemt stāvokli vai noraidīt stāvokli. Kad ievades virkne ir veiksmīgi apstrādāta un automāts sasniegs galīgo stāvokli, tas tiks pieņemts.
Ierobežots automāts sastāv no šādiem elementiem:
J: ierobežota stāvokļu kopa
∑: ierobežota ievades simbolu kopa
q0: sākotnējais stāvoklis
F: galīgais stāvoklis
d: pārejas funkcija
Pārejas funkciju var definēt kā
δ: Q x ∑ →Q
FA raksturo divos veidos:
- DFA (ierobežoti automāti)
- NDFA (nenodeterministiski galīgi automāti)
DFA
DFA apzīmē Deterministic Finite Automata. Deterministisks attiecas uz aprēķina unikalitāti. Programmā DFA ievades rakstzīme pāriet tikai uz vienu stāvokli. DFA nepieņem nulles pārvietošanu, kas nozīmē, ka DFA nevar mainīt stāvokli bez ievades rakstzīmes.
DFA ir pieci korteži {Q, ∑, q0, F, δ}
J: visu stāvokļu kopa∑: ierobežota ievades simbolu kopa, kur δ: Q x ∑ →Q
q0: sākotnējais stāvoklis
F: galīgais stāvoklis
d: pārejas funkcija
Piemērs
Skatiet deterministisko galīgo automātu piemēru:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3} 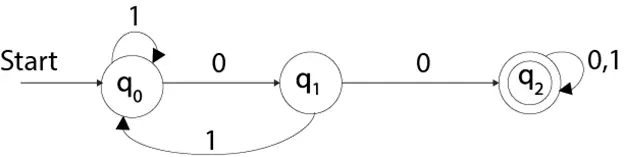
NDFA
NDFA attiecas uz nedeterministiskajiem galīgajiem automātiem. To izmanto, lai pārsūtītu neierobežotu skaitu stāvokļu konkrētai ievadei. NDFA pieņem NULL kustību, kas nozīmē, ka tā var mainīt stāvokli, nelasot simbolus.
NDFA ir arī pieci stāvokļi, kas ir tādi paši kā DFA. Taču NDFA ir atšķirīga pārejas funkcija.
NDFA pārejas funkciju var definēt šādi:
d: Q x ∑ →2JPiemērs
Skatiet nedeterministisku galīgo automātu piemēru:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3} 
