Izteicienu koks ir koks, ko izmanto dažādu izteiksmju attēlošanai. Koka datu struktūra tiek izmantota izteiksmīgo paziņojumu attēlošanai. Šajā kokā iekšējais mezgls vienmēr apzīmē operatorus.
- Lapu mezgli vienmēr apzīmē operandus.
- Darbības vienmēr tiek veiktas ar šiem operandiem.
- Operatoram, kas atrodas koka dziļumā, vienmēr ir augstākā prioritāte.
- Operatoram, kura dziļumā kokā nav daudz, vienmēr ir zemākā prioritāte salīdzinājumā ar operatoriem, kas guļ dziļumā.
- Operands vienmēr būs redzams koka dziļumā; tāpēc tas tiek uzskatīts par augstākā prioritāte starp visiem operatoriem.
- Īsāk sakot, mēs varam to apkopot, jo vērtībai, kas atrodas koka dziļumā, ir augstākā prioritāte salīdzinājumā ar citiem operatoriem, kas atrodas koka augšdaļā.
- Šo izteiksmes koku galvenais lietojums ir tāds, ka tas ir pieradis izvērtēt, analizēt un modificēt dažādie izteicieni.
- To izmanto arī, lai noskaidrotu katra operatora asociativitāti izteiksmē.
- Piemēram, operators + ir kreisās puses asociatīvais un / ir labās puses asociatīvais.
- Šīs asociativitātes dilemma ir novērsta, izmantojot izteiksmju kokus.
- Šie izteiksmju koki tiek veidoti, izmantojot bezkonteksta gramatiku.
- Mēs esam saistījuši kārtulu bezkonteksta gramatikā katras gramatikas produkcijas priekšā.
- Šie noteikumi ir zināmi arī kā semantiskie noteikumi, un, izmantojot šos semantiskos noteikumus, mēs varam viegli izveidot izteiksmju kokus.
- Tā ir viena no galvenajām kompilatora dizaina daļām un pieder semantiskās analīzes fāzei.
- Šajā semantiskajā analīzē mēs izmantosim uz sintaksi vērstus tulkojumus, un izvades veidā mēs izveidosim anotētu parsēšanas koku.
- Anotēts parsēšanas koks nav nekas cits kā vienkārša parsēšana, kas saistīta ar tipa atribūtu un katru ražošanas noteikumu.
- Izteiksmju koku izmantošanas galvenais mērķis ir izveidot sarežģītas izteiksmes, un tās var viegli novērtēt, izmantojot šos izteiksmju kokus.
- Tas ir nemainīgs, un, kad esam izveidojuši izteiksmes koku, mēs nevaram to mainīt vai modificēt tālāk.
- Lai veiktu vairāk modifikāciju, ir pilnībā jākonstruē jaunais izteiksmes koks.
- To izmanto arī, lai atrisinātu postfiksa, prefiksa un infiksa izteiksmes novērtējumu.
Izteiksmes kokiem ir ļoti svarīga loma, pārstāvot to valodas līmenī kodu datu formā, kas galvenokārt tiek glabāta kokam līdzīgā struktūrā. To izmanto arī atmiņas attēlojumā lambda izteiksme. Izmantojot koka datu struktūru, mēs varam izteikt lambda izteiksmi pārredzamāk un skaidrāk. Vispirms tas tiek izveidots, lai pārveidotu koda segmentu par datu segmentu, lai izteiksmi varētu viegli novērtēt.
Izteiksmes koks ir binārs koks, kurā katrs ārējais vai lapas mezgls atbilst operandam un katrs iekšējais vai vecākmezgls atbilst operatoriem, tāpēc, piemēram, izteiksmes koks 7 + ((1+8)*3) būtu:
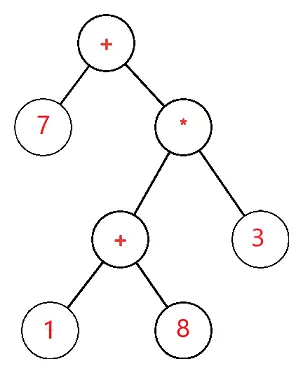
Lai S ir izteiksmes koks
Ja S nav nulle, tad
Ja S.vērtība ir operands, tad
Atgriezt S.vērtību
x = atrisināt (S.pa kreisi)
y = atrisināt (S.pa labi)
Atdeves aprēķināšana(x, y, S.vērtība)
Iepriekš minētajā piemērā izteiksmes koks izmantoja bezkonteksta gramatiku.
Mums ir daži iestudējumi, kas saistīti ar dažiem ražošanas noteikumiem šajā gramatikā, galvenokārt pazīstami kā semantiskie noteikumi . Mēs varam definēt rezultātu radīšanu no atbilstošajiem ražošanas noteikumiem, izmantojot šos semantiskos noteikumus. Šeit mēs izmantojām vērtības parametru, kas aprēķinās rezultātu un atgriezīs to gramatikas sākuma simbolā. S.left aprēķinās mezgla kreiso bērnu, un līdzīgi, izmantojot parametru S.right, var aprēķināt mezgla labo bērnu.
Izteiksmju koka izmantošana
- Izteiksmju koku izmantošanas galvenais mērķis ir izveidot sarežģītas izteiksmes, un tās var viegli novērtēt, izmantojot šos izteiksmju kokus.
- To izmanto arī, lai noskaidrotu katra operatora asociativitāti izteiksmē.
- To izmanto arī, lai atrisinātu postfiksa, prefiksa un infiksa izteiksmes novērtējumu.
Izteiksmes koka ieviešana
Lai ieviestu izteiksmes koku un uzrakstītu tā programmu, mums būs jāizmanto kaudzes datu struktūra.
Tā kā mēs zinām, ka steka pamatā ir LIFO princips, kas ir pēdējais, pirmais ārā, datu elements, kas nesen tika ievietots stekā, tiek parādīts, kad vien tas ir nepieciešams. Tās ieviešanai tiek izmantotas divas galvenās steka darbības, push un pop. Izmantojot push operāciju, datu elementu ievietosim stekā, un, izmantojot pop operāciju, datu elementu noņemsim no steka.
Galvenās steka funkcijas izteiksmes koka realizācijā:
Vispirms mēs veiksim dotās izteiksmes skenēšanu no kreisās uz labo pusi, pēc tam pa vienam pārbaudīsim identificēto rakstzīmi,
- Ja skenēta rakstzīme ir operands, mēs pielietosim push operāciju un iespiedīsim to kaudzē.
- Ja skenēta rakstzīme ir operators, mēs tai izmantosim uznirstošo darbību, lai noņemtu abas vērtības no steka un padarītu tās par tās atvasinātajām vērtībām, un pēc tam mēs atbīdīsim pašreizējo vecākmezglu atpakaļ kaudzē.
Izteiksmju koka ieviešana C programmēšanas valodā
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> Iepriekš minētās programmas rezultāts ir:
X + Y * Z / W
Izteiksmju koka ieviešana C++ programmēšanas valodā
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> Iepriekš minētās programmas rezultāts ir:
X + Y * Z / W
Izteiksmju koka ieviešana Java programmēšanas valodā
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 