1. piemērs:
Izveidojiet NFA pārejas tabulai, kā parādīts tālāk:
| Pašreizējais stāvoklis | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| q1 | q3 | e |
| q2 | q2, q3 | q3 |
| →q3 | q3 | q3 |
Risinājums:
Pārejas diagrammu var uzzīmēt, izmantojot kartēšanas funkciju, kā norādīts tabulā.
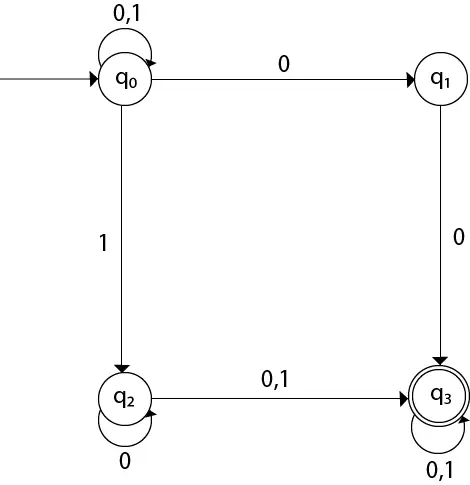
Šeit,
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} 2. piemērs:
Izveidojiet NFA ar ∑ = {0, 1}, pieņem visas virknes, kas beidzas ar 01.
java math.random
Risinājums:

Tādējādi NFA būtu:

3. piemērs:
Izveidojiet NFA ar ∑ = {0, 1}, kurā dubultā '1' seko dubultā '0'.
Risinājums:
pārvērst virkni par datumu
FA ar dubulto 1 ir šāds:

Tūlīt pēc tā ir jāraksta dubultā 0.
Tad

Tagad pirms dubultā 1 var būt jebkura virkne 0 un 1. Tāpat pēc dubultā 0 var būt jebkura virkne 0 un 1.
Tādējādi NFA kļūst:
stīgu savienošana

Tagad ņemot vērā virkni 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
4. piemērs:
Izveidojiet NFA, kurā visa virkne satur apakšvirkni 1110.
Risinājums:
Valoda sastāv no visas virknes, kas satur apakšvirkni 1010. Daļējas pārejas diagramma var būt:

Tagad kā 1010 varētu būt apakšvirkne. Tādējādi mēs pievienosim ievades 0 un 1, lai varētu saglabāt valodas apakšvirkni 1010. Tādējādi NFA kļūst:
java satur apakšvirkni

Iepriekš minētās pārejas diagrammas pārejas tabulu var sniegt zemāk:
| Pašreizējais stāvoklis | 0 | 1 |
|---|---|---|
| →q1 | q1 | q1, q2 |
| q2 | q3 | |
| q3 | q4 | |
| q4 | q5 | *q5 | q5 | q5 |
Apsveriet virkni 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
Iesprūst! Tā kā ievades simbolam 0 nav ceļa no q2. Mēs varam apstrādāt virkni 111010 citā veidā.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
Tā kā stāvoklis q5 ir pieņemšanas stāvoklis. Mēs saņemam pilnīgu skenēšanu un esam sasnieguši galīgo stāvokli.
5. piemērs:
Izveidojiet NFA ar ∑ = {0, 1} pieņem visas virknes, kurās trešais simbols no labā gala vienmēr ir 0.
char uz veselu java
Risinājums:

Tādējādi mēs vienmēr iegūstam trešo simbolu no labā gala kā “0”. NFA var būt:

Iepriekš redzamais attēls ir NFA, jo stāvoklī q0 ar ievadi 0 mēs varam pāriet uz stāvokli q0 vai q1.
