Ievietošanas kārtošana un atlases kārtošana ir divi populāri kārtošanas algoritmi, un to galvenā atšķirība ir tajā, kā tie atlasa un ievieto elementus sakārtotā secībā.
Atlases kārtošana:
- Atlases kārtošanā ievades masīvs tiek sadalīts divās daļās: sakārtotajā daļā un nešķirotajā daļā.
- Algoritms atkārtoti atrod minimālo elementu nešķirotajā daļā un apmaina to ar nešķirotās daļas vistālāk kreiso elementu, tādējādi paplašinot sakārtoto daļu par vienu elementu.
- Atlases kārtošanas laika sarežģītība visos gadījumos ir O(n^2).
Ievietošanas kārtošana:
- Ievietošanas kārtošanā arī ievades masīvs tiek sadalīts divās daļās: sakārtotajā daļā un nešķirotajā daļā.
Algoritms paņem elementu no nešķirotās daļas un novieto to pareizajā pozīcijā sakārtotajā daļā, pārvietojot lielākos elementus par vienu pozīciju pa labi.
Ievietošanas kārtošanas laika sarežģītība sliktākajā gadījumā ir O(n^2), taču tā var labāk darboties daļēji sakārtotiem masīviem, un labākā gadījuma laika sarežģītība ir O(n).
Galvenās atšķirības: - Atlases kārtošana skenē nešķiroto daļu, lai atrastu minimālo elementu, savukārt ievietošanas kārtošana skenē sakārtoto daļu, lai atrastu pareizo pozīciju elementa novietošanai.
Atlases kārtošanai nepieciešams mazāk mijmaiņas darījumu nekā ievietošanas kārtošanai, bet vairāk salīdzinājumu.
Ievietošanas kārtošana ir efektīvāka nekā atlases kārtošana, ja ievades masīvs ir daļēji vai gandrīz sakārtots, savukārt atlases kārtošana darbojas labāk, ja masīvs ir ļoti nešķirots.
Rezumējot, abiem algoritmiem ir līdzīga laika sarežģītība, taču atšķiras to izvēles un izvietošanas metodes. Izvēle starp tiem ir atkarīga no ievades datu īpašībām un konkrētās problēmas prasībām.
Ievietošanas šķirošanas priekšrocības:
- Vienkārši un viegli saprotami un īstenojami.
- Efektīva mazām datu kopām vai gandrīz sakārtotiem datiem.
- Vietas šķirošanas algoritms, kas nozīmē, ka tam nav nepieciešama papildu atmiņa.
- Stabils kārtošanas algoritms, kas nozīmē, ka tas saglabā vienādu elementu relatīvo secību ievades masīvā.
Ievietošanas šķirošanas trūkumi:
- Neefektīvs lielām datu kopām vai apgrieztās secības datiem ar sliktākā gadījuma laika sarežģītību O(n^2).
- Ievietošanas kārtošanai ir daudz mijmaiņas darījumu, kas mūsdienu datoros var palēnināt to darbību.
Atlases kārtošanas priekšrocības:
- Vienkārši un viegli saprotami un īstenojami.
- Efektīva mazām datu kopām vai gandrīz sakārtotiem datiem.
- Vietas šķirošanas algoritms, kas nozīmē, ka tam nav nepieciešama papildu atmiņa.
Atlases kārtošanas trūkumi:
- Neefektīvs lielām datu kopām ar sliktākā gadījuma laika sarežģītību O(n^2).
- Atlases kārtošanai ir daudz salīdzinājumu, kas var padarīt to lēnu mūsdienu datoros.
- Nestabils kārtošanas algoritms, kas nozīmē, ka tas var nesaglabāt vienādu elementu relatīvo secību ievades masīvā.
Šajā rakstā mēs apspriedīsim atšķirību starp ievietošanas kārtošanu un atlases kārtošanu:
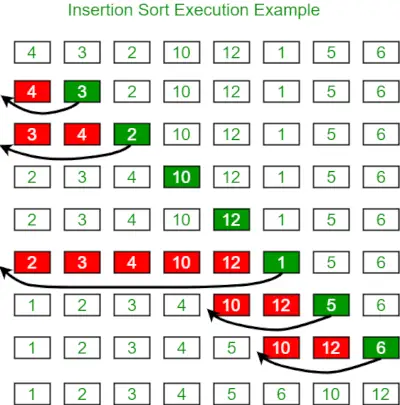
Ievietošanas kārtošana ir vienkāršs šķirošanas algoritms, kas darbojas līdzīgi tam, kā jūs kārtojat spēļu kārtis rokās. Masīvs ir praktiski sadalīts sakārtotajā un nešķirotajā daļā. Vērtības no nešķirotās daļas tiek atlasītas un novietotas pareizajā vietā sakārtotajā daļā.
Algoritms:
Lai kārtotu n izmēra masīvu augošā secībā:
- Atkārtojiet no arr[1] līdz arr[n] pa masīvu.
- Salīdziniet pašreizējo elementu (atslēgu) ar tā priekšgājēju.
- Ja galvenais elements ir mazāks par tā priekšgājēju, salīdziniet to ar iepriekšējiem elementiem. Pārvietojiet lielākos elementus par vienu pozīciju uz augšu, lai atbrīvotu vietu apmainītajam elementam.
Zemāk ir attēls, kas ilustrē ievietošanas kārtošanu:
Zemāk ir programma tam pašam:
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> taustiņš) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = atslēga; } } // Funkcija N izmēra masīva drukāšanai void printArray(int arr[], int n) { int i; // Drukāt masīvu (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
Java
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> taustiņš) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = atslēga; } } // Funkcija N izmēra masīva drukāšanai static void printArray(int arr[], int n) { int i; // Drukājiet masīvu priekš (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Draivera kods public static void main(String[ ] args) { int arr[] = { 12, 11, 13, 5, 6 }; Šo kodu nodrošina code_hunt> |
>
>
Python3
# Python 3 program for the insertion sort> # Function to sort an array using> # insertion sort> def> insertionSort(arr, n):> >i>=> 0> >key>=> 0> >j>=> 0> >for> i>in> range>(>1>,n,>1>):> >key>=> arr[i]> >j>=> i>-> 1> ># Move elements of arr[0..i-1],> ># that are greater than key to> ># one position ahead of their> ># current position> >while> (j>>> and> arr[j]>atslēga):> >arr[j>+> 1>]>=> arr[j]> >j>=> j>-> 1> >arr[j>+> 1>]>=> key> # Function to print an array of size N> def> printArray(arr, n):> >i>=> 0> ># Print the array> >for> i>in> range>(n):> >print>(arr[i],end>=> ' '>)> >print>(>'
'>,end>=> '')> # Driver Code> if> __name__>=>=> '__main__'>:> >arr>=> [>12>,>11>,>13>,>5>,>6>]> >N>=> len>(arr)> ># Function Call> >insertionSort(arr, N)> >printArray(arr, N)> > ># This code is contributed by bgangwar59.> |
>
>
C#
// C# program for the above approach> using> System;> class> GFG> {> >// Function to sort an array using> >// insertion sort> >static> void> insertionSort(>int>[] arr,>int> n)> >{> >int> i, key, j;> >for> (i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> taustiņš) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = atslēga; } } // Funkcija N izmēra masīva drukāšanai static void printArray(int[] arr, int n) { int i; // Drukāt masīvu (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // Draivera kods static public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 } int N = arr.Length // Funkcija Call insertionSort(arr, N } } // Šis kods ir); sniedza Dharanendra L V> |
>
>
Javascript
> // JavaScript program for the above approach> // Function to sort an array using> // insertion sort> function> insertionSort(arr,n)> {> >let i, key, j;> >for> (i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> taustiņš) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = atslēga; } } // Funkcija N izmēra masīva drukāšanai function printArray(arr,n) { let i; // Drukāt masīvu priekš (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Draivera kods let arr=[12, 11 , 13, 5, 6], lai N = arr.length; |
>5 6 11 12 13>
The atlases kārtošana algoritms sašķiro masīvu, atkārtoti atrodot minimālo elementu (ņemot vērā augošo secību) no nešķirotās daļas un ievietojot to sākumā. Algoritms noteiktā masīvā uztur divus apakšmasīvus.
- Apakšbloks jau ir sakārtots.
- Atlikusī apakšgrupa ir nešķirota.
Katrā atlases kārtošanas iterācijā tiek atlasīts minimālais elements (ņemot vērā augošo secību) no nešķirotā apakšgrupas un pārvietots uz sakārtoto apakšgrupu.
Tālāk ir sniegts piemērs, lai izskaidrotu iepriekš minētās darbības.
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>
Zemāk ir programma tam pašam:
C++
// C++ program for implementation of> // selection sort> #include> using> namespace> std;> // Function to swap two number> void> swap(>int>* xp,>int>* yp)> {> >int> temp = *xp;> >*xp = *yp;> >*yp = temp;> }> // Function to implement the selection> // sort> void> selectionSort(>int> arr[],>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array:
'; // Print the array printArray(arr, n); return 0; }> |
>
>
Java
// Java program for implementation of> // selection sort> import> java.util.*;> class> GFG> {> // Function to implement the selection> // sort> static> void> selectionSort(>int> arr[],>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array:
'); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995> |
>
>
Python3
# Python3 program for implementation of> # selection sort> # Function to implement the selection> # sort> def> selectionSort(arr, n):> ># One by one move boundary of> ># unsorted subarray> >for> i>in> range>(n>-> 1>):> ># Find the minimum element> ># in unsorted array> >min_idx>=> i> >for> j>in> range>(i>+> 1>, n):> >if> (arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp> |
>
>
C#
saraksts sakārtots java
// C# program for implementation of> // selection sort> using> System;> public> class> GFG> {> // Function to implement the selection> // sort> static> void> selectionSort(>int> []arr,>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array:
'); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1> |
>
>
Javascript
> // Javascript program for implementation of> // selection sort> // Function to implement the selection> // sort> function> selectionSort(arr, n)> {> >let i, j, min_idx;> > >// One by one move boundary of> >// unsorted subarray> >for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127> |
>
>Izvade:
Sorted array: 11 12 22 25 64>
Tabulas atšķirība starp ievietošanas kārtošanu un atlases kārtošanu:
| Ievietošanas kārtošana | Atlase Kārtot | |
|---|---|---|
| 1. | Ievieto vērtību iepriekš sakārtotajā masīvā, lai kārtotu vērtību kopu masīvā. | Sarakstā atrod minimālo/maksimālo skaitu un sakārto to augošā/dilstošā secībā. |
| 2. | Tas ir stabils šķirošanas algoritms. | Tas ir nestabils šķirošanas algoritms. |
| 3. | Vislabākā laika sarežģītība ir Ω(N), ja masīvs jau ir augošā secībā. Tam ir Θ (N2) sliktākajā un vidējā gadījumā. | Labākajā gadījumā sliktākajam gadījumam un vidējai atlases kārtošanai ir sarežģītība Θ (N2). |
| 4. | Šajā šķirošanas algoritmā veikto salīdzināšanas darbību skaits ir mazāks nekā veiktā mijmaiņa. | Šajā kārtošanas algoritmā veikto salīdzināšanas darbību skaits ir lielāks nekā veiktā mijmaiņa. |
| 5. | Tas ir efektīvāks par atlases kārtošanu. | Tas ir mazāk efektīvs nekā ievietošanas kārtošana. |
| 6. | Šeit elements ir zināms iepriekš, un mēs meklējam pareizo vietu, kur tos novietot. | Vieta, kur ievietot elementu, ir iepriekš zināma, mēs meklējam ievietojamo elementu šajā vietā. |
| 7. | Ievietošanas kārtošana tiek izmantota, ja:
| Atlases kārtošana tiek izmantota, kad
|
| 8. | Ievietošanas kārtošana ir adaptīva, t.i., efektīva datu kopām, kas jau ir būtiski sakārtotas: laika sarežģītība ir O (kn) kad katrs ievades elements ir ne vairāk kā k vietas tālāk no sakārtotās pozīcijas | Atlases kārtošana ir salīdzināšanas kārtošanas algoritms |
