Priekšnosacījums — datu ieguve , līdzības mērs attiecas uz attālumu ar izmēriem, kas attēlo datu objekta pazīmes datu kopā. Ja šis attālums ir mazāks, būs liela līdzības pakāpe, bet, ja attālums ir liels, līdzības pakāpe būs zema. Daži no populārajiem līdzības pasākumiem ir:
ceļojums, bet
- Eiklīda attālums.
- Manhetenas attālums.
- Žakarda līdzība.
- Minkovska attālums.
- Kosinusa līdzība.
Kosinusa līdzība ir metrika, kas palīdz noteikt, cik līdzīgi ir datu objekti neatkarīgi no to lieluma. Mēs varam izmērīt divu teikumu līdzību Python, izmantojot kosinusa līdzību. Kosinusa līdzībā datu objekti datu kopā tiek uzskatīti par vektoru. Formula, lai atrastu kosinusu līdzību starp diviem vektoriem, ir:
(x, y) = x . y / ||x|| ||y||>
kur,
- x . y = vektoru “x” un “y” reizinājums (punkts).||x|| un ||un|| = divu vektoru “x” un “y” garums (lielums).||x||
||un|| = divu vektoru “x” un “y” regulārais reizinājums. Piemērs : Apsveriet piemēru, lai atrastu līdzību starp diviem vektoriem - 'x' un 'un' , izmantojot kosinusa līdzību. “x” vektoram ir vērtības, x = {3, 2, 0, 5} “Y” vektoram ir vērtības, y = {1, 0, 0, 0} Kosinusa līdzības aprēķināšanas formula ir šāda: 
(x, y) = x. y / ||x|| ||un||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3 ||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16 ||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1 ∴ (x, y) = 3 / (6.16 * 1) = 0.49>
Atšķirību starp diviem vektoriem “x” un “y” nosaka:
∴ (x, y) = 1 - (x, y) = 1 - 0.49 = 0.51>
- Kosinusa līdzība starp diviem vektoriem tiek mērīta ar “θ”.
- Ja θ = 0°, “x” un “y” vektori pārklājas, tādējādi pierādot, ka tie ir līdzīgi.
- Ja θ = 90°, “x” un “y” vektori ir atšķirīgi.
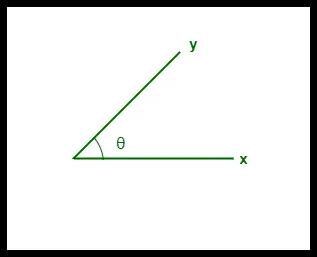
Divu vektoru kosinusa līdzība
Priekšrocības:
- Kosinusa līdzība ir izdevīga, jo pat tad, ja divi līdzīgi datu objekti atrodas tālu viens no otra Eiklīda attālumā izmēra dēļ, starp tiem joprojām var būt mazāks leņķis. Jo mazāks leņķis, jo lielāka līdzība.
- Uzzīmējot daudzdimensiju telpā, kosinusa līdzība atspoguļo datu objektu orientāciju (leņķi), nevis lielumu.