NFA var veikt nulli, vienu vai vairāk nekā vienu gājienu no noteiktā stāvokļa uz dotā ievades simbola. NFA var būt arī NULL kustības (pārvietojas bez ievades simbola). No otras puses, DFA ir viena un tikai viena kustība no noteiktā stāvokļa uz dotā ievades simbola.

Darbības, lai pārveidotu NFA par DFA:

1. darbība: konvertējiet doto NFA uz tai līdzvērtīgu pārejas tabulu
Lai pārveidotu NFA par līdzvērtīgu pārejas tabulu, mums ir jāuzskaita visi stāvokļi, ievades simboli un pārejas noteikumi. Pārejas noteikumi ir attēloti matricas veidā, kur rindas attēlo pašreizējo stāvokli, kolonnas attēlo ievades simbolu un šūnas attēlo nākamo stāvokli.

2. darbība. Izveidojiet DFA sākuma stāvokli
DFA sākuma stāvoklis ir visu iespējamo NFA sākuma stāvokļu kopa. Šo komplektu sauc par NFA sākuma stāvokļa slēgšanu. Epsilona slēgšana ir visu stāvokļu kopa, ko var sasniegt no sākuma stāvokļa, sekojot epsilona (?) pārejām.

3. darbība. Izveidojiet DFA pārejas tabulu
DFA pārejas tabula ir līdzīga NFA pārejas tabulai, taču atsevišķu stāvokļu vietā rindas un kolonnas attēlo stāvokļu kopas. Katram ievades simbolam atbilstošā šūna pārejas tabulā satur epsilona slēgšanu stāvokļu kopai, kas iegūta, ievērojot pārejas noteikumus NFA pārejas tabulā.

4. darbība. Izveidojiet DFA galīgos stāvokļus
DFA galīgie stāvokļi ir stāvokļu kopas, kurās ir vismaz viens galīgais stāvoklis no NFA.

5. darbība: vienkāršojiet DFA
Iepriekšējās darbībās iegūtajā DFA var būt nevajadzīgi stāvokļi un pārejas. Lai vienkāršotu DFA, mēs varam izmantot šādas metodes:

• Noņemt nesasniedzamos stāvokļus: stāvokļus, kurus nevar sasniegt no sākuma stāvokļa, var noņemt no DFA.
• Noņemt mirušos stāvokļus: stāvokļus, kas nevar novest pie galīgā stāvokļa, var noņemt no DFA.
• Apvienot ekvivalentos stāvokļus: stāvokļus, kuriem ir vienādi pārejas noteikumi visiem ievades simboliem, var apvienot vienā stāvoklī.

6. darbība: atkārtojiet 3.–5. darbību, līdz turpmāka vienkāršošana nav iespējama
Pēc DFA vienkāršošanas mēs atkārtojam 3.–5. darbību, līdz turpmāka vienkāršošana nav iespējama. Galīgais iegūtais DFA ir minimālais DFA ekvivalents dotajam NFA.

Piemērs: Apsveriet šādu NFA, kas parādīts 1. attēlā.

Tālāk ir norādīti dažādi NFA parametri. Q = {q0, q1, q2}? = (a, b) F = {q2}? (NFA pārejas funkcija)

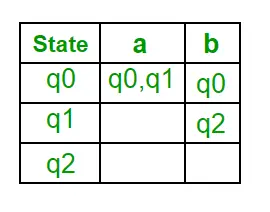
1. darbība: Q’ = ? 2. darbība: Q = {q0} 3. darbība: katram Q stāvoklim atrodiet katra ievades simbola stāvokļus. Pašlaik Q’ stāvoklis ir q0, atrodiet kustības no q0 ievades simbolā a un b, izmantojot NFA pārejas funkciju, un atjauniniet DFA pārejas tabulu. ?’ (DFA pārejas funkcija)

Tagad {q0, q1} tiks uzskatīts par vienu stāvokli. Tā kā tā ieraksts nav Q', pievienojiet to Q'. Tātad Q' = { q0, { q0, q1 } } Tagad pārejas no stāvokļa { q0, q1 } uz dažādiem ievades simboliem nav atrodamas DFA pārejas tabulā, mēs to aprēķināsim šādi: ?' ( { q0, q1 } , a ) = ? (q0, a) ? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) = ? (q0, b) ? ? ( q1, b ) = { q0, q2 } Tagad mēs atjaunināsim DFA pārejas tabulu. ?’ (DFA pārejas funkcija)

Tagad {q0, q2} tiks uzskatīts par vienu stāvokli. Tā kā tā ieraksts nav Q', pievienojiet to Q'. Tātad Q' = { q0, { q0, q1 }, { q0, q2 } } Tagad pārejas no stāvokļa {q0, q2} uz dažādiem ievades simboliem nav atrodamas DFA pārejas tabulā, mēs to aprēķināsim šādi: ?' ( { q0, q2 }, a ) = ? (q0, a) ? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) = ? (q0, b) ? ? ( q2, b ) = { q0 } Tagad mēs atjaunināsim DFA pārejas tabulu. ?’ (DFA pārejas funkcija)

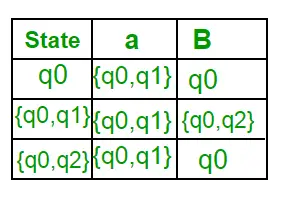
Tā kā jauns stāvoklis netiek ģenerēts, konvertēšana ir pabeigta. DFA galīgais stāvoklis būs stāvoklis, kura komponents ir q2, t.i., { q0, q2 } Tālāk ir norādīti dažādi DFA parametri. Q’ = {q0, {q0, q1}, {q0, q2}}? = ( a, b ) F = { { q0, q2 } } un pārejas funkcija ?', kā parādīts iepriekš. Iepriekš minētā NFA galīgā DFA ir parādīta 2. attēlā.

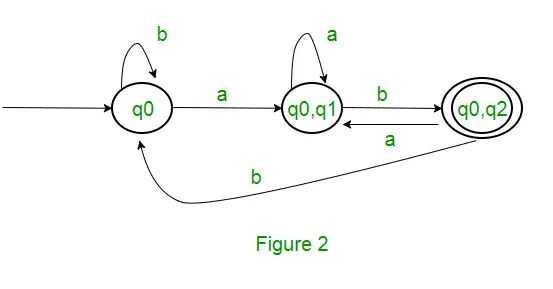
Piezīme : Dažreiz regulāro izteiksmi nav viegli pārveidot par DFA. Vispirms varat konvertēt regulāro izteiksmi uz NFA un pēc tam NFA uz DFA.

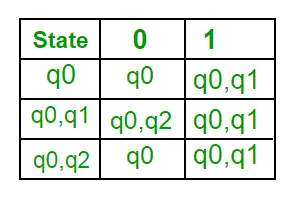
jautājums: Regulārajai izteiksmei (0 + 1)* (10) atbilstošajā minimāli determinētajā galīgajā automātā stāvokļu skaits ir ____________.

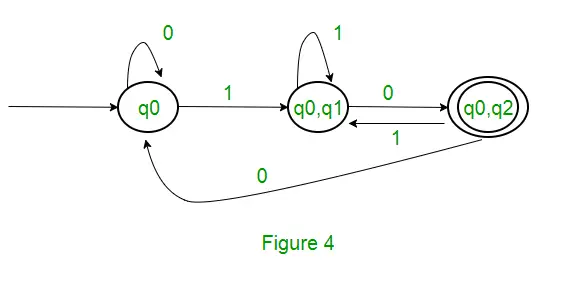
Risinājums: Pirmkārt, mēs izveidosim NFA iepriekšminētajai izteiksmei. Lai izveidotu NFA ar (0 + 1)*, NFA būs tādā pašā stāvoklī q0 ar ievades simbolu 0 vai 1. Pēc tam savienošanai mēs pievienosim divas kustības (q0 uz q1, ja ir 1, un q1 pret q2, ja ir 0), kā parādīts attēlā. 3. attēlā.

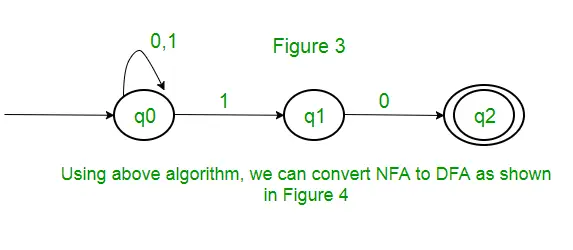
Šo rakstu ir sagatavojis Sonal Tuteja.