Reālajā pasaulē ne visiem datiem, ar kuriem mēs strādājam, ir mērķa mainīgais. Šāda veida datus nevar analizēt, izmantojot uzraudzītus mācību algoritmus. Mums ir nepieciešama nepārraudzītu algoritmu palīdzība. Viens no populārākajiem analīzes veidiem bez uzraudzības mācībās ir klientu segmentācija mērķtiecīgām reklāmām vai medicīniskajā attēlveidošanā, lai atrastu nezināmas vai jaunas inficētas zonas un daudzus citus lietošanas gadījumus, kurus mēs sīkāk apspriedīsim šajā rakstā.
Satura rādītājs
- Kas ir klasterēšana?
- Klasterizācijas veidi
- Klasterizācijas lietojumi
- Klasterizācijas algoritmu veidi
- Klasterizācijas pielietojumi dažādās jomās:
- Bieži uzdotie jautājumi (FAQ) par klasterizāciju
Kas ir klasterēšana?
Datu punktu grupēšanas uzdevumu, pamatojoties uz to līdzību, sauc par klasteru analīzi vai klasteru analīzi. Šī metode ir definēta sadaļā Mācības bez uzraudzības , kuras mērķis ir gūt ieskatu no nemarķētiem datu punktiem, tas ir, atšķirībā no uzraudzīta mācīšanās mums nav mērķa mainīgā.
Klasterizācijas mērķis ir veidot viendabīgu datu punktu grupas no neviendabīgas datu kopas. Tas novērtē līdzību, pamatojoties uz metriku, piemēram, Eiklīda attālumu, kosinusa līdzību, Manhetenas attālumu utt., un pēc tam sagrupē punktus ar augstāko līdzības punktu skaitu.
Piemēram, tālāk sniegtajā grafikā mēs varam skaidri redzēt, ka, pamatojoties uz attālumu, veidojas 3 apļveida kopas.
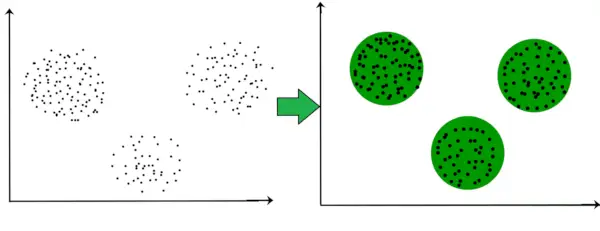
Tagad nav nepieciešams, lai izveidotajām kopām būtu apļveida forma. Klasteru forma var būt patvaļīga. Ir daudzi algoritmi, kas labi darbojas, lai noteiktu patvaļīgas formas kopas.
padarīt skriptu izpildāmu
Piemēram, zemāk dotajā grafikā redzams, ka izveidotās kopas nav apļveida formas.

Klasterizācijas veidi
Vispārīgi runājot, ir 2 veidu klasterizācijas, ko var veikt, lai grupētu līdzīgus datu punktus:
- Cietā klasterizācija: Šāda veida klasterizācijā katrs datu punkts pilnībā vai pilnībā pieder klasterim. Piemēram, pieņemsim, ka ir 4 datu punkti, un mums tie ir jāsagrupē 2 klasteros. Tātad katrs datu punkts piederēs 1. vai 2. klasterim.
| Datu punkti | Kopas |
|---|---|
| A | C1 |
| B | C2 |
| C | C2 |
| D | C1 |
- Mīkstā klasterizācija: Šāda veida klasterizācijā tā vietā, lai katru datu punktu piešķirtu atsevišķai klasterim, tiek novērtēta šī punkta iespējamība vai iespējamība, ka klasteris ir. Piemēram, pieņemsim, ka ir 4 datu punkti, un mums tie ir jāsagrupē 2 klasteros. Tātad mēs novērtēsim varbūtību, ka datu punkts pieder abām kopām. Šī varbūtība tiek aprēķināta visiem datu punktiem.
| Datu punkti | C1 varbūtība | C2 varbūtība |
| A | 0,91 | 0.09 |
| B | 0.3 | 0.7 |
| C | 0.17 | 0,83 |
| D | 1 | 0 |
Klasterizācijas lietojumi
Tagad, pirms sākam ar klasterizācijas algoritmu veidiem, mēs apskatīsim klasterizācijas algoritmu lietošanas gadījumus. Klasterizācijas algoritmus galvenokārt izmanto:
- Tirgus segmentācija – Uzņēmumi izmanto klasterus, lai grupētu savus klientus, un izmanto mērķtiecīgas reklāmas, lai piesaistītu vairāk auditorijas.
- Sociālo tīklu analīze – Sociālo mediju vietnes izmanto jūsu datus, lai izprastu jūsu pārlūkošanas uzvedību un sniegtu jums mērķtiecīgus draugu ieteikumus vai satura ieteikumus.
- Medicīniskā attēlveidošana – ārsti izmanto klasterizāciju, lai atklātu slimās vietas diagnostikas attēlos, piemēram, rentgena staros.
- Anomāliju noteikšana – Lai atrastu novirzes reāllaika datu kopas plūsmā vai prognozētu krāpnieciskus darījumus, to identificēšanai varam izmantot klasterizāciju.
- Vienkāršojiet darbu ar lielām datu kopām — katrai klasterim tiek piešķirts klastera ID pēc klasterizācijas pabeigšanas. Tagad varat samazināt visu funkciju kopas funkciju kopu tās kopas ID. Klasterizācija ir efektīva, ja tā var attēlot sarežģītu gadījumu ar vienkāršu klastera ID. Izmantojot to pašu principu, datu klasterēšana var padarīt sarežģītas datu kopas vienkāršākas.
Ir daudz vairāk klasteru izmantošanas gadījumu, taču ir daži no galvenajiem un izplatītākajiem klasteru izmantošanas gadījumiem. Tālāk mēs apspriedīsim klasterizācijas algoritmus, kas palīdzēs veikt iepriekš minētos uzdevumus.
Fredijs Merkūrijs
Klasterizācijas algoritmu veidi
Virsmas līmenī klasterizācija palīdz analizēt nestrukturētus datus. Grafika, īsākais attālums un datu punktu blīvums ir daži no elementiem, kas ietekmē klasteru veidošanos. Klasterizācija ir process, kurā nosaka, cik objekti ir saistīti, pamatojoties uz metriku, ko sauc par līdzības mēru. Līdzības metriku ir vieglāk atrast mazākās funkciju kopās. Palielinoties funkciju skaitam, kļūst grūtāk izveidot līdzības mērījumus. Atkarībā no datu ieguvē izmantotā klasterizācijas algoritma veida, lai grupētu datus no datu kopām, tiek izmantotas vairākas metodes. Šajā daļā ir aprakstītas klasterizācijas metodes. Ir dažādi klasterizācijas algoritmu veidi:
- Uz centru balstīta klasterizācija (nodalīšanas metodes)
- Uz blīvumu balstīta klasterizācija (uz modeļiem balstītas metodes)
- Uz savienojamību balstīta klasterizācija (hierarhiskā klasterizācija)
- Uz izplatīšanu balstīta klasterizācija
Mēs īsumā apskatīsim katru no šiem veidiem.
1. Sadalīšanas metodes ir vienkāršākie klasterizācijas algoritmi. Viņi grupē datu punktus, pamatojoties uz to tuvumu. Parasti šiem algoritmiem izvēlētais līdzības mērs ir Eiklīda attālums, Manhetenas attālums vai Minkovska attālums. Datu kopas ir sadalītas iepriekš noteiktā skaitā klasteru, un uz katru klasteru ir atsauce ar vērtību vektoru. Salīdzinot ar vektora vērtību, ievades datu mainīgais neatšķiras un pievienojas klasterim.
Galvenais šo algoritmu trūkums ir prasība, ka mums intuitīvi vai zinātniski (izmantojot elkoņa metodi) jānosaka klasteru skaits k, pirms jebkura klasterizācijas mašīnmācīšanās sistēma sāk piešķirt datu punktus. Neskatoties uz to, tas joprojām ir vispopulārākais klasterizācijas veids. K-nozīmē un K-medoids klasterēšana ir daži šāda veida klasterizācijas piemēri.
2. Uz blīvumu balstīta klasterizācija (uz modeļiem balstītas metodes)
Uz blīvumu balstīta klasterizācija, uz modeļiem balstīta metode, atrod grupas, pamatojoties uz datu punktu blīvumu. Pretēji uz centroīdu balstītai klasterizācijai, kas prasa, lai klasteru skaits būtu iepriekš noteikts un ir jutīgs pret inicializāciju, uz blīvumu balstīta klasterizācija automātiski nosaka klasteru skaitu un ir mazāk pakļauta sākuma pozīcijām. Tie lieliski apstrādā dažāda izmēra un formas klasterus, padarot tos ideāli piemērotus datu kopām ar neregulāras formas vai pārklājošām kopām. Šīs metodes pārvalda gan blīvus, gan retus datu reģionus, koncentrējoties uz vietējo blīvumu, un var atšķirt kopas ar dažādām morfoloģijām.
Turpretim grupēšanai, kuras pamatā ir centroīdi, tāpat kā k-vidējie, ir grūti atrast patvaļīgas formas kopas. Sakarā ar iepriekš iestatīto klasteru prasību skaitu un ārkārtējo jutīgumu pret centroīdu sākotnējo novietojumu, rezultāti var atšķirties. Turklāt uz centroīdu balstītu pieeju tendence radīt sfēriskus vai izliektus klasterus ierobežo to spēju apstrādāt sarežģītas vai neregulāras formas kopas. Noslēgumā jāsaka, ka uz blīvumu balstīta klasterizācija novērš uz centroīdiem balstītu metožu trūkumus, autonomi izvēloties klasteru izmērus, ir noturīga pret inicializāciju un veiksmīgi uztver dažāda izmēra un formas kopas. Populārākais uz blīvumu balstīts klasterizācijas algoritms ir DBSCAN .
mini rīkjosla Excel
3. Uz savienojamību balstīta klasterizācija (hierarhiskā klasterizācija)
Metode saistītu datu punktu apkopošanai hierarhiskās klasteros tiek saukta par hierarhisko klasterizāciju. Katrs datu punkts sākotnēji tiek ņemts vērā kā atsevišķs klasteris, kas pēc tam tiek apvienots ar vislīdzīgākajiem klasteriem, veidojot vienu lielu kopu, kurā ir visi datu punkti.
Padomājiet par to, kā jūs varat sakārtot priekšmetu kolekciju, pamatojoties uz to, cik tie ir līdzīgi. Katrs objekts sākas kā savs klasteris koka pamatnē, izmantojot hierarhisku klasterizāciju, kas veido dendrogrammu, kokam līdzīgu struktūru. Pēc tam, kad algoritms pārbauda, cik objekti ir līdzīgi viens otram, tuvākie klasteru pāri tiek apvienoti lielākos klasteros. Kad katrs objekts atrodas vienā klasterī koka augšpusē, apvienošanas process ir pabeigts. Dažādu precizitātes līmeņu izpēte ir viena no jautrajām lietām par hierarhisko klasteru veidošanu. Lai iegūtu noteiktu skaitu klasteru, varat izvēlēties izgriezt dendrogramma noteiktā augstumā. Jo vairāk līdzīgi divi objekti atrodas klasterī, jo tuvāk tie ir. Tas ir salīdzināms ar priekšmetu klasificēšanu pēc to dzimtas kokiem, kur tuvākie radinieki ir sagrupēti kopā un platākie zari norāda uz vispārīgākām saiknēm. Ir 2 pieejas hierarhiskajai klasterizācijai:
- Sadalošā klasterizācija : Tas atbilst lejupējai pieejai, šeit mēs uzskatām, ka visi datu punkti ir viena liela klastera daļa, un pēc tam šis klasteris tiek sadalīts mazākās grupās.
- Aglomeratīvā klasterizācija : Tiek izmantota augšupēja pieeja, šeit mēs uzskatām, ka visi datu punkti ir atsevišķu klasteru daļa, un pēc tam šie klasteri tiek apvienoti, lai izveidotu vienu lielu kopu ar visiem datu punktiem.
4. Uz izplatīšanu balstīta klasterizācija
Izmantojot uz sadalījumu balstītu klasterizāciju, datu punkti tiek ģenerēti un sakārtoti atbilstoši to tieksmei iekrist vienā un tajā pašā varbūtības sadalījumā (piemēram, Gausa, binomiālā vai citā) datos. Datu elementi tiek grupēti, izmantojot uz varbūtību balstītu sadalījumu, kura pamatā ir statistikas sadalījumi. Iekļauti datu objekti, kuriem ir lielāka iespēja būt klasterī. Ir mazāka iespēja, ka datu punkts tiks iekļauts klasterī, jo tālāk tas atrodas no klastera centrālā punkta, kas pastāv katrā klasterī.
Ievērojams uz blīvumu un robežām balstītu pieeju trūkums ir nepieciešamība a priori precizēt kopas dažiem algoritmiem un galvenokārt klasteru formas definīcija lielākajai daļai algoritmu. Ir jābūt atlasītam vismaz vienam regulējumam vai hiperparametram, un, lai gan tam ir jābūt vienkāršam, kļūdaini kļūdoties, var būt neparedzētas sekas. Uz izplatību balstītai klasterizācijai ir noteiktas priekšrocības salīdzinājumā ar tuvuma un centroīdu klasterizācijas pieejām elastības, precizitātes un klasteru struktūras ziņā. Galvenais jautājums ir tas, ka, lai izvairītos no pārmērīga pielāgošana , daudzas klasterizācijas metodes darbojas tikai ar simulētiem vai izgatavotiem datiem vai arī tad, ja lielākā daļa datu punktu noteikti pieder iepriekš iestatītam sadalījumam. Populārākais uz izplatīšanu balstīts klasterizācijas algoritms ir Gausa maisījuma modelis .
Klasterizācijas pielietojumi dažādās jomās:
- Mārketings: To var izmantot, lai raksturotu un atklātu klientu segmentus mārketinga nolūkos.
- Bioloģija: To var izmantot, lai klasificētu dažādas augu un dzīvnieku sugas.
- Bibliotēkas: To izmanto dažādu grāmatu klasterizēšanai, pamatojoties uz tēmām un informāciju.
- Apdrošināšana: To izmanto, lai atpazītu klientus, viņu politiku un identificētu krāpšanu.
- Pilsētas plānošana: To izmanto māju grupu veidošanai un to vērtību izpētei, pamatojoties uz to ģeogrāfisko atrašanās vietu un citiem klātesošajiem faktoriem.
- Zemestrīču pētījumi: Apgūstot zemestrīces skartās zonas, mēs varam noteikt bīstamās zonas.
- Attēlu apstrāde : grupēšanu var izmantot, lai grupētu līdzīgus attēlus, klasificētu attēlus, pamatojoties uz saturu, un noteiktu attēlu datu modeļus.
- Ģenētika: Klasterizāciju izmanto, lai grupētu gēnus, kuriem ir līdzīgi ekspresijas modeļi, un identificētu gēnu tīklus, kas darbojas kopā bioloģiskajos procesos.
- Finanses: Klasterizāciju izmanto, lai identificētu tirgus segmentus, pamatojoties uz klientu uzvedību, noteiktu akciju tirgus datu modeļus un analizētu risku ieguldījumu portfeļos.
- Klientu apkalpošana: Klasterizāciju izmanto, lai grupētu klientu pieprasījumus un sūdzības kategorijās, identificētu izplatītas problēmas un izstrādātu mērķtiecīgus risinājumus.
- Ražošana : klasterizāciju izmanto, lai grupētu līdzīgus produktus, optimizētu ražošanas procesus un identificētu ražošanas procesu defektus.
- Medicīniskā diagnoze: Klasterizāciju izmanto, lai grupētu pacientus ar līdzīgiem simptomiem vai slimībām, kas palīdz noteikt precīzu diagnozi un noteikt efektīvas ārstēšanas metodes.
- Krāpšanas atklāšana: Klasterizāciju izmanto, lai identificētu aizdomīgus modeļus vai anomālijas finanšu darījumos, kas var palīdzēt atklāt krāpšanu vai citus finanšu noziegumus.
- Satiksmes analīze: Klasterizāciju izmanto, lai grupētu līdzīgus satiksmes datu modeļus, piemēram, maksimālās stundas, maršrutus un ātrumus, kas var palīdzēt uzlabot transporta plānošanu un infrastruktūru.
- Sociālo tīklu analīze: Klasterizāciju izmanto, lai identificētu kopienas vai grupas sociālajos tīklos, kas var palīdzēt izprast sociālo uzvedību, ietekmi un tendences.
- Kiberdrošība: Klasterizāciju izmanto, lai grupētu līdzīgus tīkla trafika vai sistēmas uzvedības modeļus, kas var palīdzēt atklāt un novērst kiberuzbrukumus.
- Klimata analīze: Klasterizāciju izmanto, lai grupētu līdzīgus klimata datu modeļus, piemēram, temperatūru, nokrišņus un vēju, kas var palīdzēt izprast klimata pārmaiņas un to ietekmi uz vidi.
- Sporta analīze: Klasterizāciju izmanto, lai grupētu līdzīgus spēlētāju vai komandas veiktspējas datu modeļus, kas var palīdzēt analizēt spēlētāja vai komandas stiprās un vājās puses un pieņemt stratēģiskus lēmumus.
- Noziedzības analīze: Klasterizāciju izmanto, lai grupētu līdzīgus noziedzības datu modeļus, piemēram, atrašanās vietu, laiku un veidu, kas var palīdzēt identificēt noziedzības karstos punktus, paredzēt turpmākās noziedzības tendences un uzlabot noziedzības novēršanas stratēģijas.
Secinājums
Šajā rakstā mēs apspriedām klasterizāciju, tās veidus un lietojumprogrammas reālajā pasaulē. Nepārraudzītās mācībās ir jāaptver daudz vairāk, un klasteru analīze ir tikai pirmais solis. Šis raksts var palīdzēt jums sākt darbu ar klasterizācijas algoritmiem un palīdzēt iegūt jaunu projektu, ko var pievienot savam portfelim.
Bieži uzdotie jautājumi (FAQ) par klasterizāciju
J. Kāda ir labākā klasterizācijas metode?
10 populārākie klasterizācijas algoritmi ir:
- K-nozīmē klasterizāciju
- Hierarhiskā klasterizācija
- DBSCAN (uz blīvumu balstīta lietojumprogrammu telpiskā klasterizācija ar troksni)
- Gausa maisījumu modeļi (GMM)
- Aglomeratīvā klasterizācija
- Spektrālā klasterizācija
- Mean Shift klasterizācija
- Afinitātes pavairošana
- OPTIKA (punktu pasūtīšana, lai identificētu klasterizācijas struktūru)
- Bērzs (līdzsvarota iteratīva samazināšana un klasterizācija, izmantojot hierarhijas)
J. Kāda ir atšķirība starp klasterizāciju un klasifikāciju?
Galvenā atšķirība starp klasterizāciju un klasifikāciju ir tāda, ka klasifikācija ir uzraudzīts mācīšanās algoritms, bet klasterēšana ir neuzraudzīts mācīšanās algoritms. Tas nozīmē, ka mēs izmantojam klasterizāciju tām datu kopām, kurām nav mērķa mainīgā.
J. Kādas ir klasterizācijas analīzes priekšrocības?
Datus var sakārtot nozīmīgās grupās, izmantojot spēcīgu klasteru analīzes analītisko rīku. Varat to izmantot, lai precīzi noteiktu segmentus, atrastu slēptos modeļus un uzlabotu lēmumus.
mysql saraksta lietotāji
J. Kura ir ātrākā klasterizācijas metode?
K-vidējo klasterizāciju bieži uzskata par ātrāko klasterizācijas metodi tās vienkāršības un skaitļošanas efektivitātes dēļ. Tas iteratīvi piešķir datu punktus tuvākajam klastera centram, padarot to piemērotu lielām datu kopām ar zemu dimensiju un nelielu klasteru skaitu.
J. Kādi ir klasteru veidošanas ierobežojumi?
Klasterizācijas ierobežojumi ietver jutīgumu pret sākotnējiem apstākļiem, atkarību no parametru izvēles, grūtības noteikt optimālo klasteru skaitu un problēmas ar augstas dimensijas vai trokšņainu datu apstrādi.
J. No kā ir atkarīga klasterizācijas rezultāta kvalitāte?
Klasterizācijas rezultātu kvalitāte ir atkarīga no tādiem faktoriem kā algoritma izvēle, attāluma metrika, klasteru skaits, inicializācijas metode, datu pirmapstrādes metodes, klasteru novērtēšanas metrika un domēna zināšanas. Šie elementi kopā ietekmē klasterizācijas rezultāta efektivitāti un precizitāti.
