Kāršu varbūtība ir notikumu iespējamība, kas saistīta ar spēļu kāršu klāju. Kā zināms, varbūtība ir viena no svarīgākajām matemātikas tēmām, kas nodarbojas ar jebkura notikuma iespējamības aprēķināšanu. Vienkāršiem vārdiem sakot, kāršu varbūtība ir viena varbūtības daļa, kurā mēs atrodam varbūtību, ka no kāršu klāja tiks izvilkta kārts. Šajā rakstā mēs uzzināsim par kāršu varbūtību ar visu informāciju par kāršu varbūtības diagrammu, spēļu kāršu varbūtību, kā atrast kāršu varbūtību un atrisinātos kāršu varbūtības piemērus. Sāksim mācīšanos par tēmu kartes varbūtība.
Kas ir varbūtība?
Varbūtība ir matemātikas nozare, kas pēta iespējas, vai kāds notikums notiek vai nenotiek. Matemātiski nav nekas cits kā labvēlīgo iznākumu skaita attiecība pret kopējo notikuma rezultātu skaitu (izlases vieta).
Daži no reālās dzīves varbūtības piemēriem ir:
- Spēlējot kāršu spēles, lai noskaidrotu iespējamību uzvarēt vai zaudēt spēli.
- Laika prognoze, lai prognozētu lietus.
- Vēlēšanu rezultāti, lai noteiktu, vai kandidāts uzvarēs vai zaudēs.
- Eksāmena rezultāti, lai noteiktu, vai kandidāts nokārtos vai neizdosies.
Varbūtības formula
Ja E ir notikums ar paraugtelpu S un labvēlīgo iznākumu skaits ir n(E), tad notikuma E varbūtību, t.i., P(E) nosaka ar:
P(E) = n(E)/n(S)
Kas ir kartes varbūtība?
Kartes izvilkšanas vai kāršu savākšanas iespējamību no klāja sauc par kartes varbūtību. Vienkāršiem vārdiem sakot, varbūtību, kas saistīta ar spēļu kārtīm, sauc par kāršu varbūtību. Tā kā šis ir varbūtības veids, tā vienmēr ir no 0 līdz 1. Piemēram, ja mums ir jāatrod iespēja izvilkt dūzi no kāršu klāja, t.i., 4/52 = 1/13 [Tā kā ir 4 dūži 52 kāršu kavā].
Kāršu klājs varbūtībā
Kāršu klājs ir 52 kāršu kolekcija, kas, šķiet, pastāv jau tūkstošiem gadu. Tiek uzskatīts, ka kāršu vai spēļu kāršu izcelsme ir no Indijas vai Ķīnas, pirmais dokumentētais šo kāršu pierādījums ir atrodams 9.th- gadsimta Ķīna Tanu dinastijas laikā. Šīs kārtis bija līdzīgas mūsdienu kārtīm un arī tika sadalītas četros uzvalkos, taču šo uzvalku nosaukumi un simboli ir atšķirīgi, t.i., monētas, monētu virtenes, neskaitāmas un neskaitāmas desmitu kārtis.
Mūsdienās šīm kartēm ir dažādi dizaini un tās ir sadalītas četros tērpos, proti, Spade (♠), Club (♣), Heart (❤) un Diamond (◆). Vienai izvēlētajai kārtei izlases laukums, ja 52, t.i., kopējais rezultātu skaits vienai izvēlētajai kārtis no klāja ir 52.
n(S) kāršu komplektam = 52
Kāršu veidi klājā
Jebkuru kāršu klāju var klasificēt dažādos veidos, daži parametri, pēc kuriem var klasificēt kārtis, ir:
- Pamatojoties uz Krāsām
- Pamatojoties uz Suits
Sīkāk sapratīsim šo klasifikāciju šādi:
Pamatojoties uz Krāsām
Pamatojoties uz krāsām, kāršu klāju var iedalīt divās kategorijās:
- Sarkanās kartītes
- Melnās kartes
Kopumā 52 kārtis ir vienādi sadalītas sarkanajās un melnajās kārtis, kas nozīmē, ka klājā ir 26 sarkanās un 26 melnās kārtis.
Pamatojoties uz Suits
Kāršu komplektā ir četri masti:
- Sirsniņas (❤)
- Dimanti (◆)
- Klubi (♣)
- Pīķa (♠)
Izņemot šīs, ir vēl viena karšu klasifikācija, pamatojoties uz kāršu rangu:
- Ace
- Ciparu kartes
- Sejas kartes
Ace
Dūzis ir viena no šādām kārtīm, kas ir vissvarīgākā vai vismazāk svarīga, pamatojoties uz spēli. Uz tā ir uzrakstīta A kārts, un katrā mastā ir viena no šādām kārtīm, t.i., četras dūža kārtis.
Ciparu kartes
No 2 līdz 10 uz mastu ir 9 kārtis, līdz ar to kopā ir 36 šādas kārtis.
Sejas kartes
Sejas kartēs, kā norāda nosaukums, ir kartītē esošā figūra vai figūras seja. Katrai mastij ir trīs kārtis, t.i., džeks, karaliene, karalis. Tādējādi kopā ir 12 sejas kārtis.
Visas šīs klasifikācijas var redzēt nākamajā tabulā.
| Kāršu klājs (52 kārtis) | ||||
|---|---|---|---|---|
| Krāsainās kartītes | Melnās kārtis (26 kārtis) | Sarkanās kartītes (26 kārtis) | ||
| Uzvalki | Pīķa (13 kārtis) | Klubs (13 kartes) | Sirds (13 kārtis) | Dimants (13 kārtis) |
| Sejas kartes (12 kārtis klājā un 3 kārtis katrā uzvalkā) | K (karalis) | K (karalis) | K (karalis) | K (karalis) |
| Q (karaliene) | Q (karaliene) | Q (karaliene) | Q (karaliene) | |
| Dž (Džeks) | Dž (Džeks) | Dž (Džeks) | Dž (Džeks) | |
| Ciparu kartes (36 kārtis klājā un 9 kārtis uzvalkā) | 10 | 10 | 10 | 10 |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| Ace Cards (4 kārtis klājā un 1 kārts uzvalkā) | A (dūzis) | A (dūzis) | A (dūzis) | A (dūzis) |
Kāršu klāja diagramma
Spēļu kāršu klāja klasifikācija ir parādīta šajā tabulā:
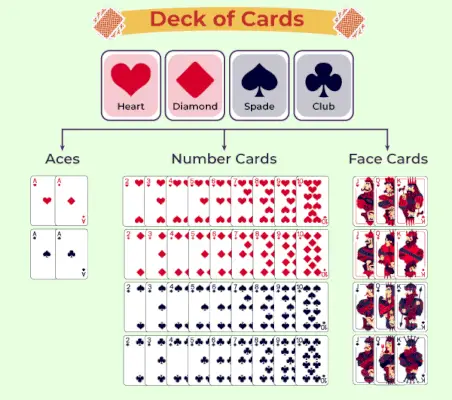
Spēļu kāršu varbūtība
Daži no izplatītākajiem notikumiem karšu varbūtībās ir aplūkoti šajā tabulā:
| Pasākums E kartes zīmēšanai | Varbūtība P(E) |
|---|---|
| Dūzis | P(E) = 4/52 = 1/13 |
| Karalis | P(E) = 4/52 = 1/13 |
| Ciparu karte | P(E) = 36/52 = 9/13 |
| Sejas karte | P(E) = 12/52 = 3/13 |
| Pīķa karte | P(E) = 13/52 = 1/4 |
| Sarkanā kartīte | P(E) = 26/52 = 1/2 |
Kā atrast karšu varbūtību?
Darbības, lai atrastu notikumu iespējamību, kas saistītas ar kartēm, ir tādas pašas kā visas pārējās varbūtības, kas norādītas šādi:
1. darbība: Vispirms atrodiet dotā jautājuma labvēlīgo iznākumu skaitu.
2. darbība: Pēc tam atrodiet kopējo rezultātu skaitu.
3. darbība: Izmantojiet varbūtības formulu, lai atrastu kartes varbūtību.
Piemērs: Kāda ir iespējamība, ka no kāršu klāja izvilks dūzi?
Atbilde:
Šeit E ir dūža kārts izvilkšanas notikums
Kopējais rezultātu skaits komplektā n(S) = 52
Labvēlīgo iznākumu skaits = n(E) = dūža kārts izvilkšana no klāja = 4 (vienā klājā ir 4 dūža kārtis)
P(E) = n(E)/n(S) = 4/52
P(E) = 1/13
Varbūtība, ka tiks izvilkta dūža kārts = 1/13
Jautājumu paraugi par kartes varbūtību
1. uzdevums. Kāda ir iespējamība, ka no kāršu klāja tiks izvilktas šādas kārtis?
(i) lāpsta
(ii) melnā karte
iii) numura karte
Risinājums:
(i) Šeit E ir lāpstas kārts izvilkšanas notikums
Kopējais rezultātu skaits komplektā n(S) = 52
Labvēlīgo iznākumu skaits = n(E) = lāpstas kārts izvilkšana no klāja = 13 (1 klājā ir 13 kārtis no katras masts)
P(E) = n(E)/n(S) = 13/52
P(E) = 1/4
Pīķa novilkšanas varbūtība = 1/4
(ii) Šeit E ir melnās kartītes izvilkšanas notikums
Kopējais rezultātu skaits komplektā n(S) = 52
Labvēlīgo iznākumu skaits = n(E) = melnās kartītes izvilkšana no klāja = 26 (vienā kāršu komplektā ir 26 melnās kārtis)
P(E) = n(E)/n(S) = 26/52
P(E) = 1/2
Melnās kartītes izvilkšanas varbūtība = 1/2
(iii) Šeit E ir numura kartes izvilkšanas notikums
Kopējais rezultātu skaits komplektā n(S) = 52
Labvēlīgo iznākumu skaits = n(E) = skaitļu kārts izvilkšana no klāja = 36 (vienā kāršu komplektā ir 36 skaitļu kārtis)
P(E) = n(E)/n(S) = 36/52
P(E) = 9/13
Ciparu kartītes izvilkšanas varbūtība = 9/13
2. uzdevums. Kāda ir iespējamība, ka no kāršu klāja tiks izvilktas šādas kārtis?
(i) karalis vai melnā kārts
(ii) sarkanā un dūža kārts
Risinājums:
(i) Šeit E ir karaļa vai melnās kārts izvilkšanas notikums
Kopējais rezultātu skaits komplektā n(S) = 52
Labvēlīgo iznākumu skaits = n(E) = karaļa vai melnās kārts izvilkšana no klāja = 26 + 2 = 28 (Ir 26 melnās kārtis, kurās 2 ir karalis un atlikušie 2 melnās kārtis 1 klājā)
P(E) = n(E)/n(S) = 28/52
P(E) = 7/13
Karaļa vai melnās kārts izvilkšanas varbūtība = 7/13
(ii) Šeit E ir sarkanās un dūža kārts izvilkšanas notikums
Kopējais rezultātu skaits komplektā n(S) = 52
Labvēlīgo iznākumu skaits = n(E) = sarkanās un dūža kārtis no klāja = 2 (ir 26 sarkanās kārtis, kurās 2 ir dūža kārtis)
Atbilstoši jautājumam izvilktajai kārtei jābūt sarkanai un abām dūzim. Tāpēc n(E) = 2
P(E) = n(E)/n(S) = 2/52
P(E) = 1/26
Sarkanās un dūža kārts izvilkšanas iespējamība= 1/26
3. uzdevums. Kāda ir iespējamība, ka no kāršu klāja tiks izvilktas šādas kārtis?
(i) Karte, kas nav kluba karte
(ii) Karte, kas nav seja
Risinājums:
(i) Šeit E ir ne-kluba kartes izņemšanas notikums
Kopējais rezultātu skaits komplektā n(S) = 52
Labvēlīgo iznākumu skaits = n(E) = kartītes, kas nav klubs, izvilkšana no klāja = 39 (vienā kāršu komplektā ir 13 nūjas, ārpus klāja = 52 – 13 = 39)
P(E) = n(E)/n(S) = 39/52
P(E) = 3/4
Ne-kluba kartes izvilkšanas varbūtība = 3/4
(ii) Šeit E ir notikums, kurā tiek izvilkta kartīte, kas nav sejas
Kopējais rezultātu skaits komplektā n(S) = 52
Labvēlīgo iznākumu skaits = n(E) = kārtis, kas nav sejas kārtis, no klāja = 40 (vienā klājā ir 12 sejas kārtis, ārpus klāja = 52 – 12 = 40)
P(E) = n(E)/n(S) = 40/52
P(E) = 10/13
Ne-kluba kartes izņemšanas varbūtība = 10/13
4. problēma: Kāda ir iespējamība, ka tiks izvilkta kartīte, kas nav ne sarkana, ne sejas kartīte?
Risinājums:
Šeit E ir notikums, kurā tiek izvilkta ne sarkanā, ne sejas kartīte
Kopējais rezultātu skaits komplektā n(S) = 52
Labvēlīgo iznākumu skaits = n(E) = no klāja netiek izņemta ne sarkana, ne sejas kārts.
Kopā sarkanās kartītes = 26
Kopā ir 12 sejas kārtis, bet 6 sarkanās kārtis jau ir noņemtas. Tātad atlikušās sejas kārtis = 12 – 6 = 6
n(E) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/52
P(E) = 8/13
Varbūtība, ka tiks uzzīmēta ne sarkanā, ne sejas kartīte = 8/13
5. uzdevums. Kāda ir iespējamība, ka no kāršu klāja tiks izvilktas divas kārtis ar nomaiņu, ja pirmā kārts ir sirds, bet otrā ir dimants?
Risinājums:
Varbūtība izvilkt pirmo kārti kā sirdi = 13/52
Pēc pirmās kartītes izvilkšanas karte tiek izņemta.
Varbūtība, ka otrā kārts tiks izvilkta kā rombs = 13/51
Varbūtība, ka pirmo kārti izvilks kā sirdi un otro kā dimantu = (13/52) × (13/51)
Varbūtība, ka pirmo kārti izvilks kā sirdi un otro kā dimantu = 13/204
Bieži uzdotie jautājumi par kartes varbūtību
1. Kas ir kartes varbūtība?
Varbūtību izvilkt karti no kāršu klāja sauc par kāršu varbūtību.
2. Uzskaitiet uzvalku veidus kāršu komplektā.
Kāršu komplektā ir četru veidu uzvalki. Viņi ir:
- Sirdis
- Dimanti
- Pīķa
- Klubi
3. Kāda ir kāršu klāja parauga vieta, ja no kāršu klāja tiek izvilkta viena kārts?
Kāršu klāja parauglaukumā, kad tiek izvilkta viena kārts, ir 52 rezultāti.
4. Uzrakstiet varbūtības noteikšanas formulu.
Formulu varbūtības noteikšanai nosaka:
pievienot virkni javaNotikuma varbūtība = labvēlīgo notikumu skaits / kopējais iznākumu skaits
VAI
P(E) = n(E)/n(S)
5. Cik sejas karšu ir kāršu komplektā?
Karšu komplektā ir 12 sejas kārtis.
