Binārā skaitļu sistēma ir skaitļu sistēma, ko izmanto, lai attēlotu dažādus skaitļus, izmantojot tikai divus simbolus 0 un 1. Vārds binārs ir atvasināts no vārda bi, kas nozīmē divi. Tāpēc šo skaitļu sistēmu sauc par bināro skaitļu sistēmu. Tādējādi binārā skaitļu sistēma ir sistēma, kurā ir tikai divi simboli.
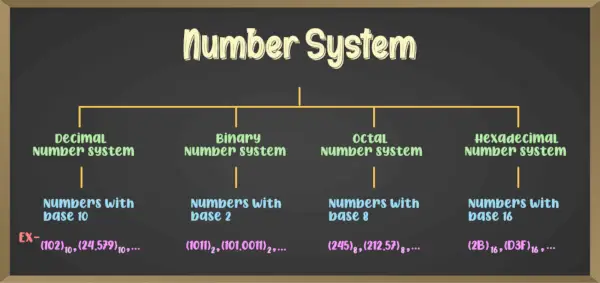
Parasti ir dažādi skaitļu sistēmu veidi, un starp tiem ir četras galvenās:
- Binārā skaitļu sistēma (skaitļu sistēma ar 2. bāzi)
- Oktālo skaitļu sistēma (ciparu sistēma ar 8. bāzi)
- Decimālā skaitļu sistēma (skaitļu sistēma ar 10. bāzi)
- Heksadecimālā skaitļu sistēma (skaitļu sistēma ar 16. bāzi)
Šeit mēs tikai uzzināsim par bināro skaitļu sistēmu. Šī numuru sistēma ir ļoti noderīga, lai izskaidrotu datoram uzdevumus. Binārajā skaitļu sistēmā mums ir divi stāvokļi 0 un 1, un šos divus stāvokļus attēlo divi tranzistora stāvokļi. Ja strāva iet caur tranzistoru, tad dators nolasa 1 un, ja tranzistorā nav strāvas, tad tas lasa 0. Tādējādi, mainot strāvu, dators nolasa bināro skaitļu sistēmu. Katrs cipars binārajā skaitļu sistēmā tiek saukts par bitu.
Šajā rakstā mēs detalizēti uzzināsim par bināro skaitļu sistēmu, bināro skaitļu sistēmas pārveidošanu, bināro tabulu, bināro skaitļu darbību, piemēriem un citiem.
Satura rādītājs
- Binārā skaitļu sistēma
- Bināro skaitļu tabula
- Binārā konvertēšana uz decimālo
- Decimāldaļas konvertēšana uz bināru
- Aritmētiskās darbības ar binārajiem skaitļiem
- Bināra skaitļa 1 un 2 papildinājums
- Bināro skaitļu sistēmas izmantošana
- Bināro skaitļu sistēmas piemērs
Binārā skaitļu sistēma
Binārā skaitļu sistēma ir skaitļu sistēma, kurā mēs izmantojam divus ciparus 0 un 1, lai veiktu visas nepieciešamās darbības. Binārajā skaitļu sistēmā mums ir bāze 2. Binārās skaitļu sistēmas bāzi sauc arī par skaitļu radiksi numuru sistēma .
Binārā skaitļu sistēmā skaitli attēlojam kā
- (11001)2
Iepriekš minētajā piemērā ir dots binārs skaitlis, kura bāze ir 2. Binārā skaitļu sistēmā katrs cipars tiek saukts par bitu. Iepriekš minētajā piemērā ir 5 cipari.
Bināro skaitļu tabula
| Decimālskaitlis | Binārais skaitlis | Decimālskaitlis | Binārais skaitlis |
|---|---|---|---|
| 1 | 001 | vienpadsmit | 1011. gads |
| 2 | 010 | 12 | 1100 |
| 3 | 011 | 13 | 1101 |
| 4 | 100 | 14 | 1110 |
| 5 | 101 | piecpadsmit | 1111 |
| 6 | 110 | 16 | 10 000 |
| 7 | 111 | 17 | 10001 |
| 8 | 1000 | 18 | 10010 |
| 9 | 1001. gads | 19 | 10011 |
| 10 | 1010. gads | divdesmit | 10100 |
Binārā konvertēšana uz decimālo
Bināro skaitli pārvērš par decimālo skaitli, reizinot katru binārā skaitļa ciparu ar pakāpju 1 vai 0 ar atbilstošo 2 pakāpju. Pieņemsim, ka bināram skaitlim ir n cipari, B = an-1…a3a2a1a0. Tagad atbilstošais decimālskaitlis tiek dots kā
D = (a n-1 ×2 n-1 ) +…+(a 3 ×2 3 ) + (a 2 ×2 2 ) + (a 1 ×2 1 ) + (a 0 ×2 0 )
Linux komandas
Apskatīsim piemēru, lai labāk izprastu jēdzienu.
Piemērs: Konvertēt (10011) 2 līdz ciparam aiz komata.
Risinājums:
Dotais binārais skaitlis ir (10011)2.
(10011)2= (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (1 × 20)
= 16 + 0 + 0 + 2 + 1 = (19)10
Tādējādi binārais skaitlis (10011)2ir izteikts kā (19)10.
Decimāldaļas konvertēšana uz bināru
Decimālskaitlis tiek pārveidots par bināru skaitli, nepārtraukti dalot doto decimālo skaitli ar 2, līdz mēs iegūstam koeficientu kā 1, un mēs rakstām skaitļus no lejupielādes uz augšu.
Apskatīsim piemēru, lai labāk izprastu jēdzienu.
Piemērs: konvertēt (28) 10 par bināro skaitli.
Risinājums:
Tādējādi (28)10ir izteikts kā (11100)2.
Aritmētiskās darbības ar binārajiem skaitļiem
Mēs varam viegli veikt dažādas darbības ar Binārajiem skaitļiem. Dažādas aritmētiskās darbības ar bināro skaitli ietver:
- Binārā pievienošana
- Binārā atņemšana
- Binārā reizināšana
- Binārais sadalījums
Tagad uzzināsim par to pašu sīkāk.
Binārā pievienošana
Divu bināro skaitļu saskaitīšanas rezultāts arī ir binārs skaitlis. Lai iegūtu divu bināro skaitļu saskaitīšanas rezultātu, mums ir jāsaskaita bināro skaitļu cipars pa ciparam. Tālāk pievienotajā tabulā parādīts binārās pievienošanas noteikums.
| Binārais skaitlis (1) | Binārais skaitlis (2) | Papildinājums | Nēsāt |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Binārā atņemšana
Divu bināro skaitļu atņemšanas rezultāts arī ir binārs skaitlis. Lai iegūtu divu bināro skaitļu atņemšanas rezultātu, bināro skaitļu cipars ir jāatņem pa ciparam. Tālāk pievienotajā tabulā parādīts binārās atņemšanas noteikums.
| Binārais skaitlis (1) | Binārais skaitlis (2) | Atņemšana | Aizņemties |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Binārā reizināšana
Bināro skaitļu reizināšanas process ir līdzīgs decimālskaitļu reizināšanai. Jebkuru divu bināro skaitļu reizināšanas noteikumi ir norādīti tabulā,
| Binārais skaitlis (1) | Binārais skaitlis (2) | Reizināšana |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Binārais sadalījums
The dalīšanas metode binārajiem skaitļiem ir līdzīga decimālskaitļu dalīšanas metodei. Apskatīsim piemēru, lai labāk izprastu jēdzienu.
Piemērs: sadalīšana (101101) 2 autors (110) 2
Risinājums:
Bināra skaitļa 1 un 2 papildinājums
- Binārā skaitļa 1 papildinājums tiek iegūts, apgriežot binārā skaitļa ciparus.
Piemērs: atrodiet (10011) 1. papildinājumu 2 .
Risinājums:
Dotais binārais skaitlis ir (10011)2
Tagad, lai atrastu tā 1 papildinājumu, mums ir jāapgriež dotā skaitļa cipari.
Tādējādi 1 papildinājums no (10011)2ir (01100)2
- Binārā skaitļa 2 papildinājumu iegūst, apgriežot binārā skaitļa ciparus un pēc tam pievienojot 1 vismazāk nozīmīgajam bitam.
Piemērs: atrodiet (1011) 2 papildinājumu 2 .
Risinājums:
Dotais binārais skaitlis ir (1011)2
Lai atrastu 2 papildinājumu, vispirms atrodiet tā 1 papildinājumu, t.i., (0100)2
Tagad, pievienojot 1 vismazāk nozīmīgajam bitam, mēs iegūstam (0101)2
Tādējādi 2. papildinājums (1011)2ir (0101)2
Bināro skaitļu sistēmas izmantošana
Bināro skaitļu sistēmas tiek izmantotas dažādiem mērķiem, un vissvarīgākais bināro skaitļu sistēmas lietojums ir:
- Bināro skaitļu sistēma tiek izmantota visā digitālajā elektronikā dažādu darbību veikšanai.
- Programmēšanas valodas datu kodēšanai un dekodēšanai izmanto bināro skaitļu sistēmu.
- Bināro skaitļu sistēma tiek izmantota datu zinātnēs dažādiem mērķiem utt.
Lasīt vairāk,
- Binārā formula
- Atšķirība starp decimālo un bināro skaitļu sistēmām
Bināro skaitļu sistēmas piemērs
1. piemērs: decimālskaitļa konvertēšana (98) 10 uz bināro.
Risinājums:
Tādējādi binārais skaitlis (98)10ir vienāds ar (1100010)2
2. piemērs: konvertēt bināro numuru (1010101) 2 uz decimālo skaitli.
Risinājums:
Dotais binārais skaitlis, (1010101)2
= (1 × 20) + (0 × 21) + (1 × 22) + (0 × 23) + (1 × 24) + (0 × 25) + (1 × 26)
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85)10
Tādējādi binārais skaitlis (1010101)2ir vienāds ar (85)10decimālajā sistēmā.
3. piemērs: sadalīšana (11110) 2 autors (101) 2
Risinājums:
4. piemērs. Pievienot (11011) 2 un (10100) 2
Risinājums:
Tādējādi (11011)2+ (10100)2= (101111)2
5. piemērs: atņemt (11010) 2 un (10110) 2
Risinājums:
Tādējādi (11010)2– (10110)2= (00100)2
6. piemērs: reizināt (1110) 2 un (1001) 2 .
Risinājums:
Tādējādi (1110)2× (1001)2= (1111110)2
Bieži uzdotie jautājumi par bināro skaitļu sistēmu
Kas ir binārā skaitļu sistēma?
Binārā skaitļu sistēma ir viena no četrām skaitļu sistēmām, ko izmanto, lai attēlotu skaitļus, izmantojot tikai divus ciparus, 0 un 1. Binārajā skaitļu sistēmā ciparus sauc par “bitiem”. Bināro skaitļu sistēmu datori izmanto dažādu aprēķinu veikšanai.
Kas ir a B tas?
Bits binārajā skaitļu sistēmā tiek definēts kā atsevišķi cipari, kuriem ir vērtība “0” vai “1”.
Kas ir Nibble?
Četru ciparu grupu sauc par Niblle.
Kas ir 10 binārā vērtība?
Binārā vērtība 10 ir (1010)2
Kādi ir ciparu sistēmu veidi?
Ir dažādi skaitļu sistēmu veidi, un daži no tiem ir,
- Binārā skaitļu sistēma
- Oktālo skaitļu sistēma
- Decimālo skaitļu sistēma
- Heksadecimālā skaitļu sistēma
Kā aprēķināt bināros skaitļus?
Bināros skaitļus aprēķina no cipariem, decimālskaitli dalot ar 2 un ierakstot atlikumu. Tad mēs sakārtojam visus atlikumus no jaunākā līdz vecākajam, lai iegūtu bināro skaitli.
Kā pievienot bināros skaitļus?
Binārie skaitļi tiek pievienoti, izmantojot tālāk norādītās formulas,
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (nēsājiet 1)






