Pirms sapratnes B koks un B+ koks atšķirības, mums būtu jāzina B koks un B+ koks atsevišķi.
Kas ir B koks?
B koks ir pašbalansējošs koks, un tas ir m-veida koks, kur m nosaka koka secību. Btree ir vispārinājums Binārās meklēšanas koks kurā mezglam var būt vairāk nekā viena atslēga un vairāk nekā divi bērni atkarībā no vērtības m . B kokā dati ir norādīti sakārtotā secībā ar zemākām vērtībām kreisajā apakškokā un augstākas vērtības labajā apakškokā.
vesels skaitlis dubultā java
B koka īpašības
Tālāk ir norādītas B koka īpašības:
- B kokā visiem lapu mezgliem jābūt vienā līmenī, savukārt binārā koka gadījumā lapu mezgli var būt dažādos līmeņos.
Izpratīsim šo īpašumu, izmantojot piemēru.
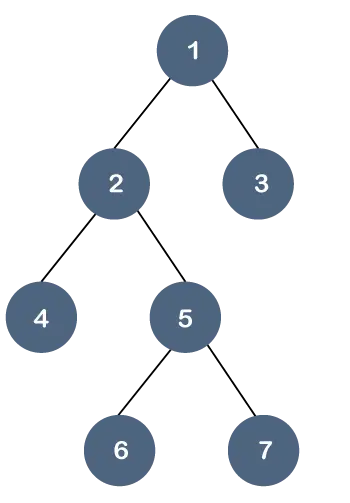
Iepriekš minētajā kokā visi lapu mezgli neatrodas vienā līmenī, taču tiem ir maksimāli divi bērni. Tāpēc mēs varam teikt, ka iepriekš minētais koks ir a binārais koks bet ne B koks.
- Ja Btree secība ir m, tad katram mezglam var būt maksimums m Minimālā bērnu skaita gadījumā lapu mezglos ir nulle bērnu, saknes mezglā ir divi bērni, un iekšējos mezglos ir m/2 griesti.
- Katram mezglam var būt maksimālās (m-1) atslēgas. Piemēram, ja m vērtība ir 5, tad atslēgu maksimālā vērtība ir 4.
- Saknes mezglam ir vismaz viena atslēga, savukārt visiem pārējiem mezgliem, izņemot saknes mezglu, ir (griesti no m/2 mīnus - 1) minimālā atslēga.
- Ja veicam ievietošanu B kokā, tad mezgls vienmēr tiek ievietots lapas mezglā.
Pieņemsim, ka mēs vēlamies izveidot 3. kārtas B koku, ievietojot vērtības no 1 līdz 10.
1. darbība: Pirmkārt, mēs izveidojam mezglu ar 1 vērtību, kā parādīts tālāk:

2. darbība: Nākamais elements ir 2, kas nāk pēc 1, kā parādīts zemāk:

3. darbība: Nākamais elements ir 3, un tas tiek ievietots pēc 2, kā parādīts zemāk:

Kā mēs zinām, ka katram mezglam var būt maksimāli 2 atslēgas, tāpēc mēs sadalīsim šo mezglu caur vidējo elementu. Vidējais elements ir 2, tāpēc tas tiek pārvietots uz vecāku. 2. mezglam nav vecāku, tāpēc tas kļūs par saknes mezglu, kā parādīts tālāk:

4. darbība: Nākamais elements ir 4. Tā kā 4 ir lielāks par 2 un 3, tas tiks pievienots pēc 3, kā parādīts tālāk:

5. darbība: Nākamais elements ir 5. Tā kā 5 ir lielāks par 2, 3 un 4, tas tiks pievienots pēc 4, kā parādīts tālāk:

Kā mēs zinām, ka katram mezglam var būt maksimāli 2 atslēgas, tāpēc mēs sadalīsim šo mezglu caur vidējo elementu. Vidējais elements ir 4, tāpēc tas tiek pārvietots uz vecāku. Vecāks ir mezgls 2; tādēļ 4 tiks pievienoti pēc 2, kā parādīts zemāk:

6. darbība: Nākamais elements ir 6. Tā kā 6 ir lielāks par 2, 4 un 5, 6 nāks pēc 5, kā parādīts zemāk:

7. darbība: Nākamais elements ir 7. Tā kā 7 ir lielāks par 2, 4, 5 un 6, tāpēc 7 nāks pēc 6, kā parādīts zemāk:

Kā mēs zinām, ka katram mezglam var būt maksimāli 2 atslēgas, tāpēc mēs sadalīsim šo mezglu caur vidējo elementu. Vidējais elements ir 6, tāpēc tas tiek pārvietots uz vecāku, kā parādīts tālāk:

Taču 6 nevar pievienot pēc 4, jo mezglam var būt maksimāli 2 atslēgas, tāpēc mēs sadalīsim šo mezglu caur vidējo elementu. Vidējais elements ir 4, tāpēc tas tiek pārvietots uz vecāku. Tā kā 4. mezglam nav vecāku, 4. mezgls kļūs par saknes mezglu, kā parādīts tālāk:

Kas ir B+ koks?
The B+ koks ir pazīstams arī kā uzlabots pašlīdzsvarots koks, jo katram ceļam no koka saknes līdz koka lapai ir vienāds garums. Šeit vienāds garums nozīmē, ka visi lapu mezgli atrodas vienā līmenī. Negadīsies, ka daži lapu mezgli atrodas trešajā līmenī un daži no tiem otrajā līmenī.
B+ koka indekss tiek uzskatīts par daudzlīmeņu indeksu, bet B+ koka struktūra nav līdzīga daudzlīmeņu indeksa secīgajiem failiem.
Kāpēc tiek izmantots B+ koks?
B+ koks tiek izmantots, lai ļoti efektīvi saglabātu ierakstus, saglabājot ierakstus indeksētā veidā, izmantojot B+ koka indeksēto struktūru. Pateicoties daudzlīmeņu indeksācijai, piekļuve datiem kļūst ātrāka un vienkāršāka.
B+ koka mezgla struktūra
B+ koka mezglu struktūrā ir norādes un galvenās vērtības, kas parādītas zemāk esošajā attēlā:

Kā mēs varam novērot iepriekš minētajā B+ koka mezgla struktūrā, tajā ir n-1 atslēgas vērtības (k1uz kn-1) un n norādes (lpp1topsn).
Meklēšanas atslēgas vērtības, kas atrodas mezglā, tiek glabātas sakārtotā secībā. Tādējādi, ja i
Ierobežojumi dažādu veidu mezgliem
Lai “b” ir B+ koka secība.
Ne-Lapu mezgls
Ļaujiet 'm' apzīmē mezgla bērnu skaitu, tad attiecību starp koka secību un bērnu skaitu var attēlot šādi:

Ļaujiet k apzīmē meklēšanas atslēgas vērtības. Sakarību starp koka secību un meklēšanas atslēgu var attēlot šādi:
Tā kā mēs zinām, ka rādītāju skaits ir vienāds ar meklēšanas atslēgas vērtībām plus 1, tāpēc matemātiski to var uzrakstīt šādi:
virknes līdz veseliem skaitļiem
Rādītāju (vai bērnu) skaits = meklēšanas taustiņu skaits + 1
Tāpēc maksimālais rādītāju skaits būtu “b”, un minimālais rādītāju skaits būtu b/2 griestu funkcija.
Lapu mezgls
Lapu mezgls ir mezgls, kas atrodas B+ koka pēdējā līmenī, un katrs lapas mezgls izmanto tikai vienu rādītāju, lai izveidotu savienojumu ar otru, lai nodrošinātu secīgu piekļuvi lapas līmenī.
Lapu mezglā maksimālais bērnu skaits ir:

Maksimālais meklēšanas taustiņu skaits ir:

Saknes mezgls
Maksimālais bērnu skaits saknes mezgla gadījumā ir: b
Minimālais bērnu skaits ir: 2
Īpaši gadījumi B+ kokā
1. gadījums: Ja saknes mezgls ir vienīgais mezgls kokā. Šajā gadījumā saknes mezgls kļūst par lapas mezglu.
Šajā gadījumā maksimālais bērnu skaits ir 1, t.i., pats saknes mezgls, savukārt minimālais bērnu skaits ir b-1, kas ir tāds pats kā lapas mezglam.
Lapas mezgla attēlojums B+ kokā

Iepriekš redzamajā attēlā '.' apzīmē rādītāju, savukārt 10, 20 un 30 ir galvenās vērtības. Rādītājs satur adresi, kurā tiek saglabāta atslēgas vērtība, kā parādīts iepriekšējā attēlā.
B+ koka piemērs

Iepriekš redzamajā attēlā mezglā ir trīs galvenās vērtības, t.i., 9, 16 un 25. Rādītājs, kas parādās pirms 9, satur atslēgas vērtības, kas ir mazākas par 9, kuras attēlo ki. Rādītājs, kas parādās pirms 16, satur galvenās vērtības, kas ir lielākas vai vienādas ar 9, bet mazākas par 16, ko attēlo kj. Rādītājs, kas parādās pirms 25, satur galvenās vērtības, kas ir lielākas vai vienādas ar 16, bet mazākas par 25, ko attēlo kn.
Atšķirības starp B koku un B+ koku

Tālāk ir norādītas atšķirības starp B koku un B+ koku:
| B koks | B+ koks |
|---|---|
| B kokā visas atslēgas un ieraksti tiek glabāti gan iekšējos, gan lapu mezglos. | B+ kokā atslēgas ir indeksi, kas tiek glabāti iekšējos mezglos, un ieraksti tiek glabāti lapu mezglos. |
| B kokā atslēgas nevar atkārtoti saglabāt, kas nozīmē, ka nav atslēgu vai ierakstu dublēšanas. | B+ kokā var būt atslēgu rašanās dublēšana. Šajā gadījumā ieraksti tiek glabāti lapu mezglos, bet atslēgas tiek glabātas iekšējos mezglos, tāpēc iekšējos mezglos var būt liekas atslēgas. |
| Btree lapu mezgli nav saistīti viens ar otru. | B+ kokā lapu mezgli ir saistīti viens ar otru, lai nodrošinātu secīgu piekļuvi. |
| Programmā Btree meklēšana nav ļoti efektīva, jo ieraksti tiek glabāti lapas vai iekšējos mezglos. | B+ kokā meklēšana ir ļoti efektīva vai ātrāka, jo visi ieraksti tiek glabāti lapu mezglos. |
| Iekšējo mezglu dzēšana ir ļoti lēns un laikietilpīgs process, jo mums jāņem vērā arī dzēstās atslēgas atvasinātais. | Dzēšana B+ kokā ir ļoti ātra, jo visi ieraksti tiek glabāti lapu mezglos, tāpēc mums nav jāņem vērā mezgla bērns. |
| Programmā Btree secīga piekļuve nav iespējama. | B+ kokā visi lapu mezgli ir savienoti viens ar otru, izmantojot rādītāju, tāpēc ir iespējama secīga piekļuve. |
| Programmā Btree tiek veikts vairāk sadalīšanas darbību, kuru dēļ augstums palielinās salīdzinājumā ar platumu, | B+ kokam ir lielāks platums nekā augstumam. |
| Programmā Btree katram mezglam ir vismaz divi zari, un katrā mezglā ir daži ieraksti, tāpēc mums nav jāpārvietojas līdz lapu mezgliem, lai iegūtu datus. | B+ kokā iekšējie mezgli satur tikai norādes, un lapu mezgli satur ierakstus. Visi lapu mezgli atrodas vienā līmenī, tāpēc mums ir jāpārvietojas līdz lapu mezgliem, lai iegūtu datus. |
| Saknes mezglā ir vismaz no 2 līdz m bērniem, kur m ir koka secība. | Saknes mezglā ir vismaz no 2 līdz m bērniem, kur m ir koka secība. |
