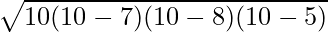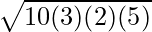Akūtā leņķa trijstūris ir trijstūris, kurā visi trīsstūru leņķi ir asi leņķi. Trijstūrim var būt tikai viens taisns leņķis vai strups leņķis trijstūra leņķa summas īpašības dēļ. Tādējādi trīsstūri, kuram visi trīs leņķi ir asi leņķi, t.i., leņķus, kuru vērtība ir mazāka par 90 grādiem, sauc par akūtu leņķi.

Pamatojoties uz trijstūra iekšējo leņķu veidiem, trijstūri var iedalīt trīs kategorijās: akūtā leņķa trijstūri, strupleņķa trijstūri un taisnleņķa trijstūri. Tagad šajā rakstā sīkāk uzzināsim par akūtā leņķa trijstūriem, to veidiem, īpašībām un citiem.

Kas ir akūtā leņķa trīsstūris?

An asa leņķa trīsstūris ir definēts kā trīsstūris, kura visi trīs iekšējie leņķi ir asi, t.i., to vērtība ir no 0° līdz 90°. Atkarībā no trijstūra veida akūtā leņķa trijstūra malu garumi var būt vienādi vai nevienlīdzīgi. Akūta leņķa trijstūris arī seko trijstūra leņķa summas īpašībai.

Zemāk redzamais attēls ir akūts leņķis trīsstūris, kura iekšējie leņķi ir 45°, 35° un 80°. Tā kā trīs iekšējie leņķi ir mazāki par 90°, dotais trīsstūris ir asa leņķa trijstūris.

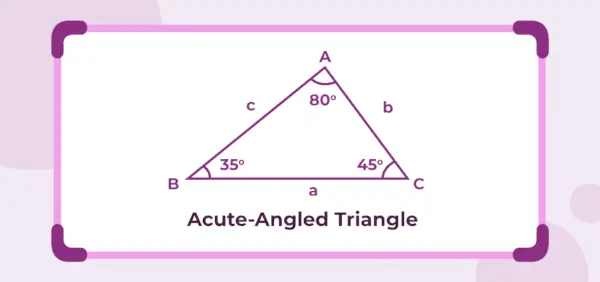
Akūta leņķa trijstūra definīcija

Akūta leņķa trijstūri ir definēti, kā norāda nosaukums, kā trijstūri, kuros visi trīs trijstūra leņķi ir asi leņķi. Akūta leņķa trīsstūru mala var būt vienāda vai nevienāda, un, pamatojoties uz to, tās tiek sadalītas trīs daļās, kas ir apskatītas tālāk esošajā rakstā.

Akūta leņķa trīsstūru veidi

Akūta leņķa trīsstūri tiek iedalīti trīs veidos atkarībā no trijstūra malu garuma,

• Vienādmalu akūts trīsstūris
• Vienādsānu akūts trīsstūris
• Skalēna akūts trīsstūris

Tagad uzzināsim par tiem sīkāk.

Vienādmalu akūts trīsstūris

Vienādmalu akūts trīsstūris, ko sauc arī par vienādmalu trijstūri, ir trijstūris, kurā visi leņķi ir asi leņķi un visi leņķi ir vienādi, arī vienādmalu akūto trijstūri malas ir vienādas. Katrs vienādmalu asa trijstūra leņķis vienmēr ir 60°.

Vienādsānu akūts trīsstūris

Vienādsānu akūts trīsstūris ir trijstūris, kurā visi leņķi ir asi leņķi un visi divi trijstūra leņķi un tiem atbilstošā mala ir vienādi. Tas ir, vienādsānu akūtā trīsstūrī mums ir divas malas un to attiecīgie leņķi ir vienādi.

Skalēna akūts trīsstūris

Skalēna akūts trīsstūris ir trijstūris, kurā visi leņķi ir asi leņķi un nav divu leņķu un nevienas malas, kas nav vienādas. Tas ir, skalēna akūtā trīsstūrī mums nav malu un leņķu, kas vienādi.

Akūtā leņķa trijstūra īpašības

Tālāk ir norādītas dažas svarīgas akūtā leņķa trīsstūra īpašības,

• Akūtā leņķa trijstūra iekšējie leņķi ir asi leņķi, t.i., leņķi ir lielāki par 0°, bet mazāki par 90°.
• Akūtā leņķa trijstūra iekšējie leņķi atbilst leņķa summas īpašībai, t.i., akūtā leņķa trijstūra leņķu summa ir 180°.
• Vienādmalu trīsstūris vienmēr ir akūtstūra trīsstūris, jo katrs vienādmalu trijstūra iekšējais leņķis ir 60°.
• Trijstūris nevar vienlaikus būt taisnleņķa trijstūris un akūtstūra trīsstūris.
• Trijstūris nevar vienlaikus būt smailleņķa trijstūris un strupleņķa trīsstūris.
• Akūtā leņķa trijstūrī mala, kas ir pretēja mazākajam leņķim, ir mazākā un arī tā pretēja ir patiesa.
• Tāpat lielākajam leņķim pretēja puse ir vislielākā, un arī tās otrādi ir taisnība.

Akūta leņķa trijstūra formulas

Laukums un perimetrs ir divas akūtā leņķa trijstūra pamatformulas, kas ir aplūkotas turpmāk.

Akūta leņķa trijstūra perimetrs

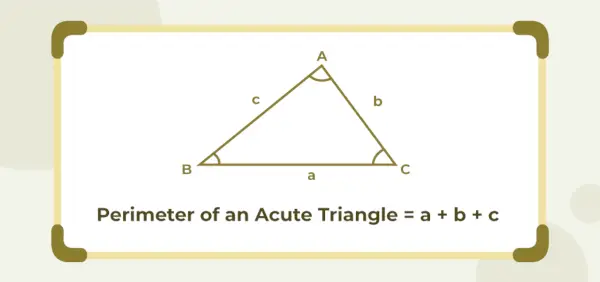
Akūta leņķa trijstūra perimetrs ir vienāds ar tā trīs malu garumu summu. Ja a, b un c ir asa leņķa trijstūra malu garumi, tad tā perimetru uzrāda kā (a + b + c) vienības.

java regulārajā izteiksmē

Akūtā leņķa trijstūra perimetrs = (a + b + c) vienības

Kur a , b , un c ir trijstūra malu garumi.

Lasīt vairāk, Trijstūra perimetrs

Akūta leņķa trijstūra laukums

Trijstūra laukumu definē kā kopējo telpu, ko aptver jebkura trīsstūra trīs malas divdimensiju plaknē.

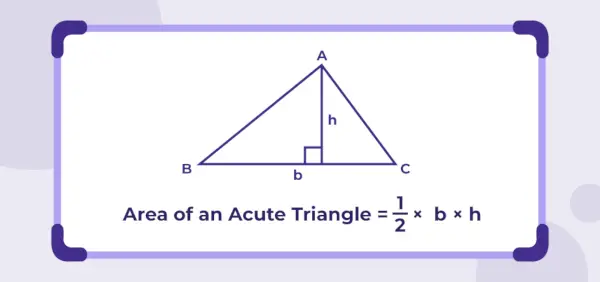
Akūtā leņķa trijstūra laukums = ½ × b × h

kur,

b ir pamatnes garums un h ir trijstūra augstums.

Lasīt vairāk, Trīsstūra laukums

Akūts trīsstūra laukums pēc Gārņa formulas

Ja ir norādīti akūtā leņķa trijstūra trīs malu garumi, tad tā laukumu var aprēķināt, izmantojot Herona formulu.

Akūtā leņķa trijstūra laukums =

kur,

s ir pusperimetrs un s = (a + b + c)/2 , tu, b , un c ir trijstūra malu garumi.

Lasīt vairāk, Gārņa formula

Svarīgas trīsstūra terminoloģijas

Dažādās terminoloģijas, kas saistītas ar akūtā leņķa trīsstūri, ir šādas:

Ap centru

Apļa centru, kas šķērso trīs trijstūra virsotnes, sauc par trijstūra apkārtmēru. To aprēķina, ņemot vērā perpendikulārās bisektrise krustošanās punktu. Akūtā leņķa trijstūrī apkārtmērs vienmēr atrodas trijstūra iekšpusē.

mašīnraksta bultiņas funkcija

Incent

Apļa centru, kas pieskaras trijstūra trim malām, sauc par trijstūra centru. To aprēķina, ņemot leņķiskās bisektora krustpunktu. Akūta leņķa trijstūra centrējums vienmēr atrodas trijstūra iekšpusē.

Centroīds

Trijstūra viduspunktu krustpunktu sauc par trijstūra centroīdu. Akūta leņķa trijstūra gadījumā trijstūra centroīds vienmēr atrodas trijstūra iekšpusē.

Ortocentrs

Trijstūra augstuma krustošanās punktu sauc par trijstūra ortocentru. Akūta leņķa trijstūra gadījumā trijstūra ortocentrs vienmēr atrodas trīsstūra iekšpusē.

Atrisināti piemēri par asa leņķa trīsstūri

1. piemērs. Kurš no šiem leņķiem var veidot akūtā leņķa trīsstūri?

a) 65°, 75°, 50° b) 95°, 40°, 45° c) 70°, 40°, 70° d) 90°, 45°, 45°

Risinājums:

Mēs zinām, ka visi akūtā leņķa trijstūra leņķi ir asi leņķi, kas nozīmē, ka to mērs ir mazāks par 90 grādiem.

Tie arī ievēro trīsstūra leņķu summas īpašību, t.i., visi to leņķi summējas līdz 180 grādiem.

a) 65°, 75°, 50°

Šeit visi leņķi ir asi leņķi, bet tas neatbilst leņķu summas īpašībai, tāpēc trīsstūris nav iespējams.

65°+ 75°+ 50° = 190° (trijstūris nav iespējams)

b) 95°, 40°, 45°

Šeit trīsstūris ir iespējams, jo tas seko trijstūra leņķu summai, t.i.

95°+40°+45° = 180

Bet, novērojot trijstūra leņķus, mēs atradām neasu leņķi 95°. Tādējādi trīsstūris nav akūtā leņķa trīsstūris.

c) 70°, 40°, 70°

Šeit trīsstūris ir iespējams, jo tas seko trijstūra leņķu summai, t.i.

mini rīkjosla Excel

70°+ 40°+ 70° = 180

Un, novērojot trijstūra leņķus, mēs atklājām, ka visi leņķi ir asi leņķi. Tādējādi trīsstūris ir akūtā leņķa trīsstūris.

d) 90°, 45°, 45°

Šeit trīsstūris ir iespējams, jo tas seko trijstūra leņķu summai, t.i.

90°+45°+45° = 180

Bet, novērojot trijstūra leņķus, mēs atradām taisnu leņķi 90°. Tādējādi trīsstūris nav akūtā leņķa trīsstūris.

2. piemērs. Atrodiet perimetru akūtam trīsstūrim XYZ, kura malas ir XY = 8 vienības, YZ = 5 vienības un XZ = 9 vienības.

Risinājums:

Ņemot vērā,

Akūta leņķa trijstūra malas,

• XY(x) = 8 vienības
• YZ(y) = 5 vienības
• XZ(z) = 9 vienības

Mēs to zinām,

Akūtā leņķa trijstūra (P) perimetrs = x + y + z

⇒ P = (8 + 5 + 9) vienības

⇒ P = 22 vienības

Tādējādi akūtā leņķa trijstūra perimetrs ir 22 vienības.

3. piemērs. Atrodiet laukumu akūtam trīsstūrim, kura augstums ir 12 vienības un pamatne ir 15 vienības.

Risinājums:

Ņemot vērā,

• Trijstūra augstums (h) = 12 vienības
• Trijstūra (b) pamatnes garums = 15 vienības

Mēs to zinām,

Trijstūra laukums (A) = ½ × b × h

⇒ A = ½ × 12 × 15

⇒ A = ½ × 180

⇒ A = 90 kvadrātvienības.

Tādējādi dotā akūtā trijstūra laukums ir 90 kvadrātvienības.

unordered_map c++

4. piemērs: atrodiet laukumu akūtam trīsstūrim, kura malas ir AB = 5 cm, BC = 7 cm un AC = 8 cm.

Risinājums:

Ņemot vērā,

Akūta leņķa trijstūra malas,

• AB = c = 5 vienības
• BC = a = 7 vienības
• AC = b = 8 vienības

Mēs to zinām,

Trijstūra laukums =

tipa liešana un tipa konvertēšana java

⇒ A =

⇒ A =

⇒ A = √(300) kv.cm

⇒ A = 10√3 kv.cm

Tātad dotā akūtā trijstūra laukums ir 10√3 kv.cm.

Bieži uzdotie jautājumi par akūtu leņķisko trīsstūri

Q1: Kas ir akūti leņķi?

Atbilde:

Leņķi, kas svārstās no 0° līdz 90°, sauc par asajiem leņķiem. Tas nozīmē, ka akūtā leņķa minimālā vērtība ir lielāka par 0° un maksimālā akūta leņķa vērtība ir lielāka par 90°.

Q2: Kas ir akūtā leņķa trīsstūris?

Atbilde:

Akūta leņķa trijstūris ir trijstūris, kura visi trīs iekšējie leņķi ir asi leņķi, t.i., leņķa vērtība ir no 0° līdz 90°.

Q3: Vai vienādmalu trīsstūris vienmēr ir akūtstūrains trīsstūris?

Atbilde:

Jā, vienādmalu trīsstūris vienmēr ir akūts leņķa trijstūris. Akūtā leņķa trijstūri ir leņķi, kuriem visiem leņķiem ir akūti leņķi, un vienādsānu trijstūrī visi leņķi ir 60°, t.i., asi leņķi. Tādējādi vienādmalu trijstūris vienmēr ir akūtstūra trīsstūris.

Q4: Kādi ir dažādi akūtā leņķa trijstūri?

Atbilde:

Akūta leņķa trijstūri ir iedalīti trīs veidos, kas ir:

• Skalēna akūts trīsstūris
• Vienādsānu akūts trīsstūris
• Vienādmalu akūts trīsstūris

Q5: Kā uzzināt, vai trijstūris ir akūtstūrains trīsstūris?

Atbilde:

Trijstūri, kura iekšējie leņķi ir mazāki par 90°, t.i., visi iekšējie leņķi ir asi leņķi, tad trijstūri sauc par akūtu leņķi. Mēs varam pārbaudīt, vai trīsstūris ir akūtstūra trīsstūris, vienkārši novērojot trijstūra leņķus.