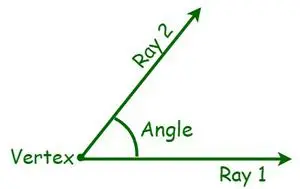
Ģeometrijā leņķis ir būtisks ģeometriskās formas mērījums. Leņķis ir definēts kā rotācijas pakāpe ap krustošanās punktu starp divām taisnēm vai plaknēm, kas nepieciešamas, lai viena atbilstu otrai. Ir dažādi leņķu veidi, kuru pamatā ir leņķa mērījumi. To mēra grādos vai radiānos. Leņķis ir forma, ko veido divas līnijas vai stari, kas atšķiras no kopīga punkta, ko sauc par virsotni. Kad tiek krustoti divi stari, t.i., projicējot puslīnijas ar kopīgu beigu punktu, veidojas leņķis. Tagad kopējos galapunktus sauc par virsotnēm, savukārt starus sauc par rokām.
Leņķu veidi

- Akūts leņķis: Akūts leņķis ir leņķis, kas ir lielāks par 0 grādiem un mazāks par 90 grādiem, t.i., tas svārstās no 0° līdz 90° (abi neskaitāmi).
- Pareizā leņķī: Taisns leņķis tiek saukts par leņķi, kas mēra tieši 90 grādus.
- Strups leņķis: Strups leņķis ir leņķis, kas ir lielāks par 90 grādiem un mazāks par 180 grādiem, t.i., tas svārstās no 90° līdz 180° (abi atsevišķi).
- Taisns leņķis: Taisns leņķis tiek saukts par leņķi, kas mēra tieši 180 grādus.
- Refleksa leņķis: Refleksa leņķis ir leņķis, kas ir lielāks par 180 grādiem un mazāks par 360 grādiem, t.i., tas svārstās no 180° līdz 360° (abi ekskluzīvi).
- Pilns leņķis vai pilna rotācija: Pilns leņķis tiek saukts par leņķi, kas mēra tieši 360 grādus.
Ir arī citi leņķu veidi, piemēram, papildleņķi, papildu leņķi un blakus esošie un neblakus esošie leņķi.
- Papildu leņķi: Tiek uzskatīts, ka divi leņķi ir viens otru papildinoši, ja to summa ir taisns leņķis, t.i., 90°.
- Papildu leņķi: Tiek uzskatīts, ka divi leņķi ir papildinoši, ja to summa ir vienāda ar 180°.
- Blakus esošie leņķi: Tiek uzskatīts, ka divi leņķi atrodas blakus, ja tiem ir kopīga virsotne un kopīga plecs.
- Leņķi, kas nav blakus: Tiek uzskatīts, ka divi leņķi nav blakus, ja tiem nav kopīgas virsotnes un kopīgas rokas.
Formula leņķu atrašanai
Ir dažāda veida formulas leņķa atrašanai; dažas no tām ir centrālā leņķa formula, dubultleņķa formula, pusleņķa formula, saliktā leņķa formula, iekšējā leņķa formula utt.
- Mēs izmantojam centrālā leņķa formulu, lai noteiktu riņķa segmenta leņķi.
- Mēs izmantojam iekšējo leņķu formulas summu, lai noteiktu trūkstošo leņķi daudzstūrī.
- Mēs izmantojam trigonometriskās attiecības, lai atrastu trūkstošo taisnleņķa trīsstūra leņķi.
- Mēs izmantojam sinusu likumu vai kosinusu likumu, lai atrastu netaisnā leņķa trīsstūra trūkstošo leņķi.
Formulas nosaukums | Formula | Kā atrast nezināmu leņķi? |
|---|---|---|
| Centrālā leņķa formula | θ =(s × 360°)/2prŠeit s ir loka garums un r ir apļa rādiuss | Aizstājiet loka garuma un apļa rādiusa vērtības, lai noteiktu riņķa segmenta leņķi. |
| Iekšējo leņķu summa Formula | 180° (n-2)Šeit n ir daudzstūra malu skaits | Lai noteiktu nezināmo daudzstūra iekšējo leņķi, vispirms, izmantojot šo formulu, aprēķiniet visu iekšējo leņķu summu un pēc tam no rezultāta atņemiet visu zināmo leņķu summu. |
| Trigonometriskās attiecības | sin θ = pretējā puse/hipotenūzacos θ = blakus esošā puse/hipotenūzaiedegums θ = pretējā puse/blakuspuse | Atkarībā no pieejamajām divām taisnleņķa trijstūra malām izvēlieties vienu no šīm trigonometriskajām attiecībām, lai atrastu nezināmo leņķi. |
| Sinusa likums | a/sin A = b/sin B = c/sin CŠeit A, B un C ir trijstūra iekšējie leņķi un a, b un c ir to attiecīgās pretējās malas. | Ja ir zināmas divas malas un neieskaitīts leņķis (vai) divi leņķi un neieskaitīta mala, tad ar sinusa likumu var noteikt trijstūra nezināmos leņķus. |
| Kosinusu likums | a2= b2+ c2– 2bc cos Ab2= c2+ a2– 2ca cos Bc2= a2+ b2– 2ab cos CŠeit A, B un C ir trijstūra iekšējie leņķi un a, b un c ir to attiecīgās pretējās malas. ir īpašs raksturs | Ja zinām trīs malas (vai) divas malas un iekļauto leņķi, tad kosinusu likumu var izmantot, lai noteiktu nezināmos trijstūra leņķus. |
Jautājumu paraugi
1. jautājums: Atrodiet leņķi dotā trīsstūra virsotnē B, izmantojot kādu no trigonometriskajām formulām leņķu atrašanai.

Risinājums:
Ņemot vērā,
BC = 3 vienības = θ blakus esošā puse.
AC = 4 vienības = θ pretējā puse.
Šajā gadījumā mēs zinām gan pretējās, gan blakus esošās θ malas. Tādējādi mēs varam izmantot pieskares formulu, lai atrastu θ.
⇒ iedegums θ = pretējā puse/blakuspuse
⇒ iedegums θ = 4/3
⇒ θ = iedegums-1(4/3) ⇒ θ = 53,1°
Tādējādi leņķis virsotnē B ir 53,1°.
2. jautājums: atrodiet leņķus virsotnēs X un Y, ja ∠Z = 35° un x = 3 collas, y = 8 collas un z = 3,5 collas.

Risinājums:
Ņemot vērā,
∠Z = 35° un x = 6 collas, y = 3 collas un z = 3,5 collas
Tā kā mēs zinām visas trīs malas un leņķi, mēs varam izmantot sinusa likuma formulu.
No sinusa likuma formulas mums ir
x/sin X = y/sin Y = z/sin Z
Tagad
y/sin Y = z/sin Z
⇒ 3/sin Y = 3,5/sin 35°
⇒ 3/bez Y = 3,5/0,574 {Tā kā grēks 35° = 0,574}
⇒ sin Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = grēks−1(0,492) = 29,47°
Mēs zinām, ka trīs leņķu summa trīsstūrī ir 180°.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29,47° + 35° = 180°
⇒ ∠X = 180° – 64,47° = 115,53°
Tādējādi ∠X = 115,53° un ∠Y = 29,47°.
3. jautājums: Aprēķiniet piecstūra piekto iekšējo leņķi, ja četri tā iekšējie leņķi ir 110°, 85°, 136° un 105°.
Risinājums:
Piecstūra malu skaits (n) = 5.
Tagad visu 5 piecstūra iekšējo leņķu summa = 180 (n -2)°
= 180 (5–2)° = 540°.
Doto 4 iekšējo leņķu summa = 110°+ 85°+ 136°+ un 105°= 436°.
imessage spēles Android ierīcēmTātad, piektais iekšējais leņķis = 540° – 436° = 104°
Tādējādi piecstūra piektais iekšējais leņķis ir 104°.
4. jautājums: nosakiet y vērtību un arī leņķu mēru dotajā attēlā.

Risinājums:
No dotā attēla var novērot, ka (4y – 6)° un (3y + 5)° ir komplementāri leņķi, t.i., (4y – 6)° un (3y + 5)° summa ir 90 °.
⇒ (4 g – 6)° + (3 g + 5)° = 90°
pārvērst char par virkni java⇒ (7 g – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Tagad (4 g – 6)° = (4 × 13–6)° = (52–6)° = 46°
(3 g + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44 °
5. jautājums: Atrodiet leņķi virsotnē Q dotajā trīsstūrī, izmantojot kādu no leņķu atrašanas formulām.

Risinājums:
Ņemot vērā, p = QR = 6 cm, q = PR = 9 cm un r = PQ = 7 cm.
Tā kā mēs zinām visas trīs malas un leņķi, mēs varam izmantot kosinusa likuma formulu, lai atrastu leņķa virsotni Q.
⇒ q2= p2+ r2– 2pr cos Q
⇒ 92= 62+72– 2 (6) (7) cos Q
⇒ 81 = 36 + 49 - 84 cos Q
⇒ 81 = 85 - 84cos Q
⇒84 cos Q = 81–85
⇒ 84 cos Q = -4
⇒ cos Q = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92,72°
Tādējādi leņķis virsotnē Q, ∠Q = 92,72°.
6. jautājums: Aprēķiniet riņķa līnijas segmenta leņķi, ja loka garums ir 12π un rādiuss ir 9 cm.
Risinājums:
Ņemot vērā,
Loka garums = 12π
Rādiuss (r) = 9 cm
Tagad leņķa formula ir:
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12 × 360°/10
⇒ θ = 240°
Tādējādi leņķis ir 240°.
