Šajā rakstā mēs apspriedīsim koka šķērsošanu datu struktūrā. Termins “koka šķērsošana” nozīmē katra koka mezgla šķērsošanu vai apmeklēšanu. Ir viens veids, kā šķērsot lineāro datu struktūru, piemēram, saistīto sarakstu, rindu un steks. Tā kā ir vairāki veidi, kā šķērsot koku, kas ir uzskaitīti šādi:
- Iepriekšpasūtīšanas šķērsošana
- Kārtības šķērsošana
- Pasta pasūtījumu šķērsošana
Tāpēc šajā rakstā mēs apspriedīsim iepriekš uzskaitītos paņēmienus, kā šķērsot koku. Tagad sāksim apspriest koku šķērsošanas veidus.
Iepriekšpasūtīšanas šķērsošana
Šis paņēmiens atbilst “kreisās labās puses saknes” politikai. Tas nozīmē, ka pirmais saknes mezgls tiek apmeklēts, pēc tam rekursīvi tiek šķērsots kreisais apakškoks un, visbeidzot, rekursīvi tiek šķērsots labais apakškoks. Tā kā saknes mezgls tiek šķērsots pirms (vai pirms) kreisā un labā apakškoka, to sauc par priekšpasūtīšanas šķērsošanu.
Tātad, veicot priekšpasūtīšanu, katrs mezgls tiek apmeklēts pirms abiem tā apakškokiem.
Iepriekšpasūtīšanas šķērsošanas pieteikumi ietver:
- To izmanto, lai izveidotu koka kopiju.
- To var arī izmantot, lai iegūtu izteiksmes koka prefiksa izteiksmi.
Algoritms
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Piemērs
Tagad apskatīsim priekšpasūtīšanas šķērsošanas tehnikas piemēru.
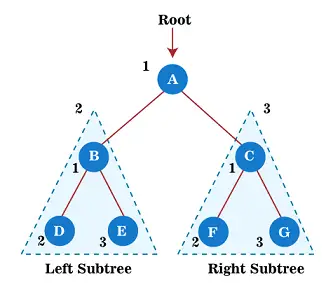
Tagad sāciet lietot priekšpasūtīšanas šķērsošanu iepriekš minētajā kokā. Pirmkārt, mēs šķērsojam saknes mezglu A; pēc tam pārejiet uz tā kreiso apakškoku B , kas tiks cauri arī pēc iepriekšēja pasūtījuma.
Tātad kreisajam apakškokam B, pirmkārt, saknes mezgls B tiek šķērsota pati; pēc tam tā kreisais apakškoks D tiek šķērsots. Kopš mezgla D nav bērnu, pāriet uz labo apakškoku UN . Tā kā mezglam E arī nav bērnu, saknes mezgla A kreisā apakškoka šķērsošana ir pabeigta.
noņemot pēdējo commit git
Tagad virzieties uz saknes mezgla A labo apakškoku, kas ir C. Tātad labajam apakškokam C vispirms saknes mezglu C ir šķērsojis sevi; pēc tam tā kreisais apakškoks F tiek šķērsots. Kopš mezgla F nav bērnu, pārejiet uz labo apakškoku G . Tā kā mezglam G arī nav bērnu, saknes mezgla A labā apakškoka šķērsošana ir pabeigta.
Tāpēc tiek šķērsoti visi koka mezgli. Tātad iepriekšminētā koka priekšpasūtīšanas šķērsošanas rezultāts ir -
A → B → D → E → C → F → G
Lai uzzinātu vairāk par priekšpasūtīšanas šķērsošanu datu struktūrā, varat sekot saitei Iepriekšpasūtīšanas šķērsošana .
Pasta pasūtījumu šķērsošana
Šis paņēmiens atbilst “kreisās-labās saknes” politikai. Tas nozīmē, ka saknes mezgla pirmais kreisais apakškoks tiek šķērsots, pēc tam rekursīvi šķērso labo apakškoku un visbeidzot tiek šķērsots saknes mezgls. Tā kā saknes mezgls tiek šķērsots aiz kreisā un labā apakškoka (vai pēc tam), to sauc par postorder traversal.
Tātad, veicot postorder šķērsošanu, katrs mezgls tiek apmeklēts pēc abiem tā apakškokiem.
ievietošanas kārtošanas algoritms
Pēc pasūtījuma šķērsošanas pielietojumi ietver:
- To izmanto, lai izdzēstu koku.
- To var izmantot arī, lai iegūtu izteiksmes koka postfix izteiksmi.
Algoritms
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Piemērs
Tagad apskatīsim piemēru par postorder traversal tehniku.

Tagad sāciet lietot postorder šķērsošanu iepriekš minētajā kokā. Vispirms mēs šķērsojam kreiso apakškoku B, kas tiks šķērsots pēc kārtas. Pēc tam mēs šķērsosim pareizo apakškoku C pēc pasūtījuma. Un visbeidzot, iepriekš minētā koka saknes mezgls, t.i., A , tiek šķērsots.
formāta java virkne
Tātad kreisajam apakškokam B, pirmkārt, tā kreisais apakškoks D tiek šķērsots. Kopš mezgla D nav bērnu, šķērsojiet pareizo apakškoku UN . Tā kā mezglam E arī nav bērnu, pārejiet uz saknes mezglu B. Pēc mezgla šķērsošanas B, saknes mezgla A kreisā apakškoka šķērsošana ir pabeigta.
Tagad virzieties uz saknes mezgla A labo apakškoku, kas ir C. Tātad labajam apakškokam C vispirms tā kreisais apakškoks F tiek šķērsots. Kopš mezgla F nav bērnu, šķērsojiet pareizo apakškoku G . Tā kā mezglam G arī nav bērnu, tāpēc, visbeidzot, labā apakškoka saknes mezgls, t.i., C, tiek šķērsots. Saknes mezgla A labā apakškoka šķērsošana ir pabeigta.
Beidzot šķērsojiet dotā koka saknes mezglu, t.i., A . Pēc saknes mezgla šķērsošanas tiek pabeigta dotā koka pēckārtas šķērsošana.
Tāpēc tiek šķērsoti visi koka mezgli. Tātad, iepriekšminētā koka šķērsošanas pēc kārtas rezultāts ir -
D → E → B → F → G → C → A
Lai uzzinātu vairāk par pēcpasūtīšanas šķērsošanu datu struktūrā, varat sekot saitei Pasta pasūtījumu šķērsošana .
Kārtības šķērsošana
Šis paņēmiens atbilst “kreisās saknes labās puses” politikai. Tas nozīmē, ka pēc saknes mezgla šķērsošanas tiek apmeklēts pirmais kreisais apakškoks un, visbeidzot, tiek šķērsots labais apakškoks. Tā kā saknes mezgls tiek šķērsots starp kreiso un labo apakškoku, to sauc par inorder traversal.
Tātad secības šķērsošanā katrs mezgls tiek apmeklēts starp tā apakškokiem.
Inorder traversal lietojumprogrammas ietver:
- To izmanto, lai iegūtu BST mezglus augošā secībā.
- To var arī izmantot, lai iegūtu izteiksmes koka prefiksa izteiksmi.
Algoritms
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Piemērs
Tagad apskatīsim Inorder šķērsošanas tehnikas piemēru.

Tagad sāciet piemērot secības šķērsošanu iepriekšminētajam kokam. Pirmkārt, mēs šķērsojam kreiso apakškoku B kas tiks šķērsoti secībā. Pēc tam mēs šķērsosim saknes mezglu A . Un visbeidzot pareizais apakškoks C tiek šķērsots secībā.
Tātad kreisajam apakškokam B , pirmkārt, tā kreisais apakškoks D tiek šķērsots. Kopš mezgla D nav bērnu, tāpēc pēc tā šķērsošanas mezgls B tiks šķērsots un, visbeidzot, mezgla B labais apakškoks, tas ir UN , tiek šķērsots. Arī mezglam E nav bērnu; tāpēc saknes mezgla A kreisā apakškoka šķērsošana ir pabeigta.
Pēc tam šķērsojiet dotā koka saknes mezglu, t.i., A .
Beidzot virzieties uz saknes mezgla A labo apakškoku, kas ir C. Tātad labajam apakškokam C; pirmkārt, tā kreisais apakškoks F tiek šķērsots. Kopš mezgla F nav bērnu, mezgls C tiks šķērsots un, visbeidzot, mezgla C labais apakškoks, tas ir, G , tiek šķērsots. Arī mezglam G nav bērnu; tāpēc saknes mezgla A labā apakškoka šķērsošana ir pabeigta.
Tā kā visi koka mezgli ir šķērsoti, dotā koka kārtas šķērsošana ir pabeigta. Iepriekš minētā koka šķērsošanas secībā rezultāts ir -
D → B → E → A → F → C → G
Lai uzzinātu vairāk par secības apbraukšanu datu struktūrā, varat sekot saitei Pasūtījuma šķērsošana .
... java
Koku šķērsošanas paņēmienu sarežģītība
Iepriekš apspriesto koku šķērsošanas metožu laika sarežģītība ir O(n) , kur 'n' ir binārā koka izmērs.
Tā kā iepriekš apspriesto koku šķērsošanas metožu kosmosa sarežģītība ir O(1) ja neņemam vērā funkciju izsaukumu steka lielumu. Pretējā gadījumā šo metožu kosmosa sarežģītība ir O(h) , kur 'h' ir koka augstums.
Koku šķērsošanas īstenošana
Tagad apskatīsim iepriekš apspriesto paņēmienu ieviešanu, izmantojot dažādas programmēšanas valodas.
Programma: Uzrakstiet programmu koku šķērsošanas tehnikas ieviešanai C valodā.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Izvade

Programma: Uzrakstiet programmu koku šķērsošanas tehnikas ieviešanai C# valodā.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Izvade

Programma: Uzrakstiet programmu koku šķērsošanas tehnikas ieviešanai C++ valodā.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Izvade
f filmas
Pēc iepriekš minētā koda izpildes izvade būs -

Secinājums
Šajā rakstā mēs esam apsprieduši dažādus koku šķērsošanas paņēmienu veidus: priekšpasūtīšanas šķērsošanu, inorder šķērsošanu un postorder šķērsošanu. Mēs esam redzējuši šīs metodes kopā ar algoritmu, piemēru, sarežģītību un ieviešanu C, C++, C# un java.
Tātad, tas viss par rakstu. Cerams, ka tas jums būs noderīgs un informatīvs.
