Jebkuram objektam, ko varat redzēt vai pieskarties, var izmērīt trīs izmērus, garumu, platumu un augstumu. Ir noteikti mūsu mājas, kurā mēs dzīvojam, izmēri. Taisnstūra displeja ekrānam/monitoram, kuru skatāties, ir tā garums un platums. Katrai trīsdimensiju ģeometriskai struktūrai tiek mērīts virsmas laukums un tilpums.
Aera, ko sedz objekta virsma, ir jebkura konkrētā objekta virsmas laukums. Tā kā objektā pieejamās vietas daudzums ir tilpums.
Satura rādītājs
- Virsmas laukums
- Kopējais virsmas laukums
- Izliektas virsmas laukums/sānu virsmas laukums
- Skaļums
- Piemēri par virsmas laukumiem un tilpumiem
- Bieži uzdotie jautājumi par virsmas laukuma un tilpuma formulām
Virsmas laukums
Virsmas laukumu un tilpumu var aprēķināt jebkurai trīsdimensiju (3D) ģeometriskai formai. Jebkuras zonas virsma ir reģions, ko aizņem objekta virsma. Tilpums ir objektā pieejamās vietas daudzums. Mums ir dažāda veida formas, piemēram, puslode, sfēra, kubs, kuboīds, cilindrs utt. Visām trīsdimensiju formām ir laukums un tilpums. Bet divdimensiju formas, piemēram, kvadrāti, taisnstūri, trīsstūri, apļi utt.
Šeit divdimensionāli mēs varam izmērīt tikai laukumu. Laukumu, ko trīsdimensiju objekta aizņem tā ārējā virsma, sauc par virsmas laukumu. To mēra kvadrātveida vienībās.
Teritorija ir divu veidu:
- Kopējais virsmas laukums
- Izliektas virsmas laukums/sānu virsmas laukums
Kopējais virsmas laukums
Laukums, ieskaitot pamatni(-es) un izliekto daļu, atbilst kopējam virsmas laukumam. Tas ir platības apjoms, ko aptver objekta virsma. Ja veidlapai ir izliekta pamatne un virsma, tad abu reģionu summa būtu kopējā platība. Kopējo virsmas laukumu var definēt kā kopējo platību, ko aptver objekts, ieskaitot tā pamatni, kā arī izliekto daļu. Ja objektam ir gan pamatne, gan izliekts laukums, tad kopējais virsmas laukums būs vienāds ar pamatnes un izliektā laukuma summu.
- Kopējā virsmas laukums ir objekta kopējā platība.
- Piemēram, par piemēru ņemiet kuboīdu, kuram ir 6 skaldnes, 12 malas un 8 virsotnes.
Kopējais virsmas laukums = bāzes laukums + izliekts laukums
Salman Khan Khan vecums
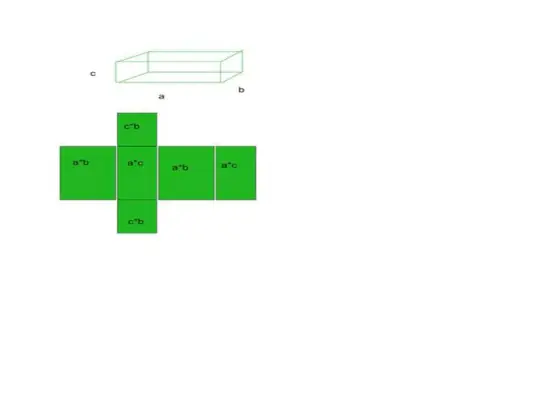
- Visu šo 6 laukumu summa būs mūsu konkrētās formas kopējās virsmas laukums
Piemērs:
Zemāk ir dots kuboīds, kura izmērs ir norādīts kā garums = 8 cm, platums = 4 cm un augstums = 6 cm, atrodiet kuboīda TSA
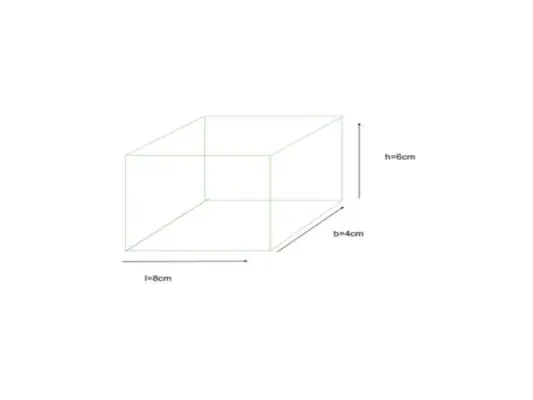
dots l = 8cm, b = 4cm, h = 6cm
TSA = 2 ((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2(104)
= 208
Kuboīda TSA ir 208 cm.
Izliektas virsmas laukums/sānu virsmas laukums
Izliektās virsmas laukums, izņemot tās centru, atbilst tikai formas(-u) izliektās daļas laukumam. Tādām formām kā konuss to bieži sauc par sānu virsmas laukumu. Sānu virsmas laukumu var definēt kā laukumu, kas ietver tikai objekta izliektās virsmas laukumu vai objekta sānu virsmas laukumu, izslēdzot objekta pamatlaukumu. Sānu virsmas laukums ir pazīstams arī kā izliektās virsmas laukums.
Lielākā daļa formu vai objektu attiecas uz izliektās virsmas laukumu, forma vai objektiem līdzīgs cilindrs norāda uz to kā sānu virsmas laukumu. Vienkārši sakot, mums redzamo laukumu sauc par sānu virsmas laukumu. Piemēram, apsveriet cilindru, kā parādīts zemāk esošajā attēlā.
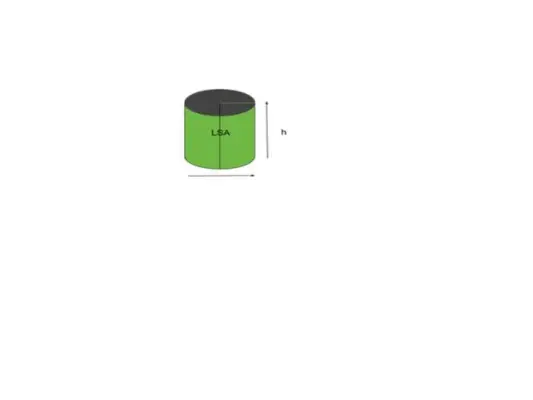
Skaļums
Tilpums ir vietas daudzums noteiktā 3D objektā. Kopējo telpas daudzumu, ko objekts vai viela aizņem, sauc par tilpumu. To mēra kubikvienībās.
Virsmas laukuma un tilpuma formulas
Dotajā tabulā ir norādīts kopējais virsmas laukums, izliektās virsmas laukums/sānu virsmas laukums un dažādu formu tilpums.
| Formas nosaukums | Izliektas virsmas laukums | Kopējais virsmas laukums | Skaļums |
|---|---|---|---|
| Kuboīds | 2h(l+b) | 2 (lb + bh + hl) | l * b * h |
| Kubs | 4a2 | 6a2 | a3 |
| Cilindrs | 2πrh | 2π(r + h) | πr2h |
| Sfēra | 4πr2 Govinda aktieris | 4πr2 | 4/3π r3 |
| Konuss | πrl | πr(r + l) | 1/3π r2h |
| Puslode | 2pr2 | 3πr2 | 2/3π r3 |
Lasīt vairāk:
- Piramīdas virsmas laukums
- Cilindra virsmas laukums
- Puslodes virsmas laukums
- Sfēras virsmas laukums
- Kuboīda virsmas laukums
Piemēri par virsmas laukumiem un tilpumiem
1. piemērs: 2 kubi, katrs ar tilpumu 512 cm 3 ir savienoti no gala līdz galam. Atrodiet iegūtā kuboīda virsmas laukumu?
Risinājums:
Ņemot vērā,
Katra kuba tilpums (V) ir = 512 cm3
tagad mēs varam norādīt, ka a3= 512 cm3
∴ Kuba mala, t.i., a = 8 cm
Tagad iegūtā kuboīda platums un garums būs 8 cm, bet augstums būs 16 cm.
Tātad kuboīda virsmas laukums (TSA) = 2 (lb + bh + lh)
Tagad, liekot vērtības, mēs iegūstam,
= 2 (8 × 16 + 8 × 8 + 16 × 8) cm 2
= (2 × 320) = 640 cm 2
Tādējādi kuboīda TSA = 640 cm 2
2. piemērs: mums ir cilindriska svece, kuras diametrs ir 14 cm un garums 2 cm. To izkausē, veidojot kubveida sveci, kuras izmēri ir 7 cm × 11 cm × 1 cm. Cik kubveida sveces var iegūt?
Risinājums:
Cilindriskās sveces izmēri:
Cilindriskās sveces rādiuss = 14/2 cm = 7 cm
Augstums/biezums = 2 cm
Vienas cilindriskas sveces tilpums = πr2h = π x 7 x 7 x (2) cm3= 308 cm3.
Kuboīda tilpums svece = 7 x 11 x 1 = 77 cm3
Tādējādi kubveida sveču skaits = kubveida sveces tilpums / vienas cilindriskas sveces tilpums = 308/77 = 4
Tādējādi mēs varam iegūt 4 kubveida formas sveces.
3. piemērs. Sieviete vēlas no māla uzbūvēt sfērisku rotaļlietu bumbu, kuras rādiuss ir vienāds ar viņas nēsātās rokassprādzes rādiusu. Ņemot vērā, ka aprocei ir apļveida forma, viņa arī vēlas, lai aproces laukums būtu vienāds ar sfēras tilpumu. Vai uzzināt, kādu rādiusu viņa valkā aproces?
Risinājums:
Lai r ir aproces rādiuss, kā arī sfēra,
Mums ir noteikts, ka sfēras tilpums ir vienāds ar aproces laukumu:
Tāpēc
πr2= 4/3 πr3
⇒ r = 3/4
Tādējādi aproces rādiuss ir 3/4 vienības.
4. piemērs: Ir dots, ka taisnā riņķveida konusa slīpuma augstums ir 25 cm un augstums ir 24 cm. Atrodi konusa izliekto virsmas laukumu?
Risinājums:
Konusa izliektās virsmas laukuma formula ir πrl. Kur r ir konusa rādiuss un l ir konusa slīpais augstums.
Šeit konuss ir labais apļveida konuss.
Tātad konusa rādiuss būtu:
r= sqrt{l^2 – h^2}
=>r = sqrt{25^2–24^2}
=> r = 7 cm.
Tagad, aprēķinot izliekto virsmu, ir:
Nepieciešamais laukums = (22/7) * 7 * 25 = 550 cm2
objektu masīvs javaTādējādi konusa izliektās virsmas laukums ir 550 cm 2 .
5. piemērs. Atrodiet sānu virsmas laukumu cilindram, kura pamatnes rādiuss ir 6 collas un augstums 14 collas.
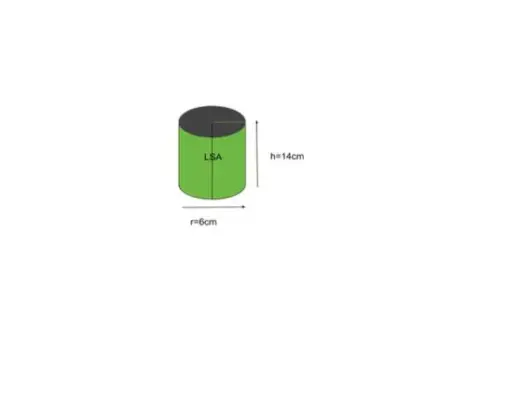
Risinājums:
Dotais rādiuss r = 6, augstums h = 14
LSA = 2∏rh
= 2 * ∏ * 6 * 14
= 168∏
= 527 787
= 528.
Dotā cilindra LSA ir 528 cm .
Praktizējiet jautājumu par virsmas laukumiem un tilpumiem
Dažādi Praktizējiet jautājumus par virsmas laukumiem un tilpumu formulas ir:
Q1. Atrodiet kuba virsmas laukumu, kura malas garums ir 5 centimetri.
Q2. Aprēķiniet sfēras tilpumu ar rādiusu 3 metri.
Q3. Nosakiet cilindra, kura rādiuss ir 4 centimetri un augstums 8 centimetri, kopējo virsmas laukumu.
Q4. Atrodiet konusa tilpumu ar rādiusu 6 collas un augstumu 10 collas.
Q5. Aprēķiniet virsmas laukumu taisnstūra prizmai, kuras garums ir 7 metri, platums 4 metri un augstums 6 metri.
Bieži uzdotie jautājumi par virsmas laukuma un tilpuma formulām
Kādas ir virsmas laukuma un tilpuma formulas?
Iepriekš minētajā rakstā ir pievienotas dažādas virsmas laukuma un tilpuma formulas.
Kāda ir virsmas laukuma tilpuma 10. klases formula?
Formula virsmas laukumam un tilpuma klasei 10 satur:
| Formas nosaukums | Izliektas virsmas laukums | Kopējais virsmas laukums | Skaļums |
|---|---|---|---|
| Kuboīds bināro koku piemēri | 2h(l+b) | 2 (lb + bh + hl) | l × b × h |
| Kubs | 4a2 | 6a2 | a3 |
| Cilindrs | 2πrh | 2π(r + h) | πr2h |
| Sfēra | 4πr2 | 4πr2 | 4/3π r3 |
| Konuss | πrl | πr(r + l) | 1/3π r2h |
| Puslode | 2pr2 | 3πr2 | 2/3π r3 |
Kāda ir kuboīda formula virsmas laukumā un tilpumā?
- Kuboīda virsmas laukums = 2 (lb + bh + hl)
- Kubioda tilpums = l × b × h
Kas ir virsmas laukums un tilpums?
Virsmas laukums ir visu cietās vielas virsmu laukums, un tās tilpums ir laukums, ko aizņem sloīds.
