Rekursīvo funkciju var definēt kā rutīnu, kas izsauc sevi tieši vai netieši.

Citiem vārdiem sakot, rekursīvā funkcija ir funkcija, kas atrisina problēmu, atrisinot mazākus vienas un tās pašas problēmas gadījumus. Šo paņēmienu parasti izmanto programmēšanā, lai atrisinātu problēmas, kuras var iedalīt vienkāršākos līdzīgos apakšproblēmās.

celtnieka dizaina modelis

Nepieciešama rekursīva funkcija:

Rekursīvā funkcija ir funkcija, kas atrisina problēmu, atrisinot mazākus vienas un tās pašas problēmas gadījumus. Šo paņēmienu bieži izmanto programmēšanā, lai atrisinātu problēmas, kuras var sadalīt vienkāršākos, līdzīgās apakšproblēmās.

1. Sarežģītu uzdevumu risināšana:

Rekursīvās funkcijas sadala sarežģītas problēmas mazākos vienas un tās pašas problēmas gadījumos, kā rezultātā tiek izveidots kompakts un lasāms kods.

2. Skaldi un valdi:

Rekursīvās funkcijas ir piemērotas dalīšanas un pārvaldīšanas algoritmiem, piemēram, sapludināšanas kārtošanai un ātrai kārtošanai, problēmu sadalīšanai mazākās apakšproblēmās, rekursīvai risināšanai un risinājumu sapludināšanai ar sākotnējo problēmu.

3. Atkāpšanās :

Rekursīvā atkāpšanās ir ideāli piemērota tādu problēmu izpētei un risināšanai kā N-Queens un Sudoku.

4. Dinamisks programmēšana:

Rekursīvās funkcijas efektīvi risina dinamiskas programmēšanas problēmas, risinot apakšproblēmas un apvienojot to risinājumus pilnā risinājumā.

dinamiskā programmēšana

5. Koks un grafiku struktūras:

Rekursīvās funkcijas ir lieliski piemērotas darbam ar koku un grafiku struktūrām, vienkāršojot pārvietošanās un rakstu atpazīšanas uzdevumus .

Kā uzrakstīt rekursīvo funkciju:

Rekursīvās funkcijas sastāvdaļas:

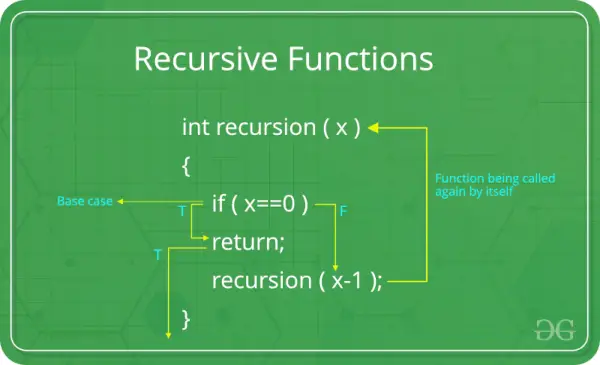
Pamata gadījums: Katrai rekursīvai funkcijai ir jābūt bāzes gadījumam. Bāzes gadījums ir vienkāršākais scenārijs, kam nav nepieciešama turpmāka atkārtošanās. Šis ir pārtraukšanas nosacījums, kas neļauj funkcijai sevi izsaukt bezgalīgi. Bez atbilstoša pamata gadījuma rekursīva funkcija var izraisīt bezgalīgu rekursiju.

nulles

Rekursīvs gadījums: Rekursīvajā gadījumā funkcija izsauc sevi ar modificētajiem argumentiem. Tāda ir rekursijas būtība – lielākas problēmas risināšana, sadalot to mazākos vienas un tās pašas problēmas gadījumos. Rekursīvajam gadījumam ar katru iterāciju jāvirzās tuvāk bāzes gadījumam.

Apskatīsim piemēru skaitļu faktoriāls :

Šajā piemērā bāzes gadījums ir kad n ir 0 , un funkcija atgriežas 1 . Rekursīvais gadījums reizina n ar ar parametru izsauktās funkcijas rezultātu n-1 . Process turpinās, līdz tiek sasniegts bāzes gadījums.

Ir svarīgi nodrošināt, lai rekursīvajai funkcijai būtu pareizs pamatgadījums un lai rekursīvie izsaukumi ved uz bāzes gadījumu, pretējā gadījumā procedūra var darboties bezgalīgi, izraisot steka pārpildīšanu (pārsniedzot funkciju izsaukumiem atvēlēto pieejamo atmiņu).

Tālāk ir parādīta skaitļa faktoriāla ieviešana:

#include  using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) {  // Base case  if (n == 0) {  return 1;  }  // Recursive case  return n * factorial(n - 1); } // Driver Code int main() {  int n = 4;  cout << 'Factorial of ' << n  << ' is:' << factorial(n);  return 0; }>

import java.util.Scanner; public class Factorial {  // Recursive Function to calculate the factorial of a number  static int factorial(int n) {  // Base case: If n is 0, the factorial is 1.  if (n == 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1);  }  public static void main(String[] args) {  int n = 4;  // Calculate and print the factorial of n.  int result = factorial(n);  System.out.println('Factorial of ' + n + ' is: ' + result);  } }>

# Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))>

using System; class Program {  // Recursive Function to calculate Factorial of a number  static int Factorial(int n)  {  // Base case  if (n == 0)  {  return 1;  }  // Recursive case  return n * Factorial(n - 1);  }  // Driver Code  static void Main()  {  int n = 4;  Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n));  } }>

// Function to calculate the factorial of a number using recursion function factorial(n) {  // Base case: If n is 0, the factorial is 1.  if (n === 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1); } // Main function function main() {  // Given number  let n = 4;  // Calculate the factorial of n.  let result = factorial(n);  // Print the result  console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();>

Factorial of 4 is:24>

Laika sarežģītība: O(n)
Palīgtelpa: O(n)

pavasara mākonis