Kvantiļu-kvantiļu (q-q diagramma) diagramma ir grafiska metode, lai noteiktu, vai datu kopa atbilst noteiktam varbūtības sadalījumam vai arī divi datu paraugi ir iegūti no viena un tā paša. populācija vai nē. Q-Q diagrammas ir īpaši noderīgas, lai novērtētu, vai datu kopa ir tāda parasti izplatīts vai ja tas seko kādam citam zināmam sadalījumam. Tos parasti izmanto statistikā, datu analīzē un kvalitātes kontrolē, lai pārbaudītu pieņēmumus un noteiktu novirzes no paredzamā sadalījuma.
Kvantiles un procentiles
Kvantiles ir punkti datu kopā, kas sadala datus intervālos, kuros ir vienādas varbūtības vai kopējā sadalījuma proporcijas. Tos bieži izmanto, lai aprakstītu datu kopas izplatību vai izplatību. Visizplatītākās kvantiles ir:
- Mediāna (50. procentile) : mediāna ir datu kopas vidējā vērtība, ja tā ir sakārtota no mazākās uz lielāko. Tas sadala datu kopu divās vienādās daļās.
- Kvartiles (25., 50. un 75. procentile) : kvartiles sadala datu kopu četrās vienādās daļās. Pirmā kvartile (Q1) ir vērtība, zem kuras ir 25% datu, otrā kvartile (Q2) ir mediāna, bet trešā kvartile (Q3) ir vērtība, zem kuras ir 75% datu.
- Procentiles : Procentiles ir līdzīgas kvartilēm, bet sadala datu kopu 100 vienādās daļās. Piemēram, 90. procentile ir vērtība, zem kuras ir 90% datu.
Piezīme:
- Q-q diagramma ir pirmās datu kopas kvantiļu diagramma attiecībā pret otrās datu kopas kvantilēm.
- Atsauces nolūkos tiek uzzīmēta arī 45% līnija; Priekš ja paraugi ir no vienas un tās pašas populācijas, tad punkti atrodas pa šo līniju.
Normāls sadalījums:
Normālais sadalījums (pazīstams arī kā Gausa sadalījuma Bell līkne) ir nepārtraukts varbūtības sadalījums, kas atspoguļo sadalījumu, kas iegūts no nejauši ģenerētajām reālajām vērtībām.
. 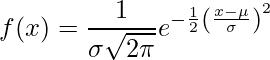

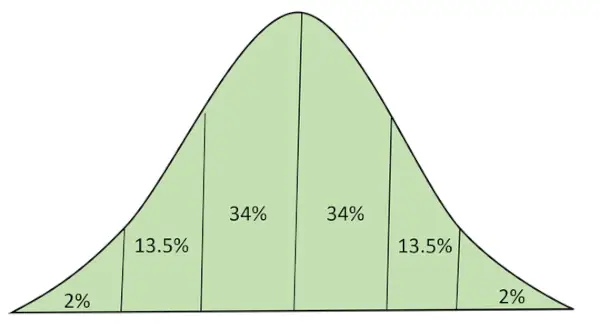
Normāls sadalījums ar laukumu zem līknes
Kā uzzīmēt Q-Q sižetu?
Lai uzzīmētu kvantiles-kvantiles (Q-Q) diagrammu, varat veikt šādas darbības:
- Savākt datus : apkopojiet datu kopu, kurai vēlaties izveidot Q-Q diagrammu. Pārliecinieties, ka dati ir skaitliski un ir izlases veida izlase no interesējošās kopas.
- Kārtojiet datus : sakārtojiet datus augošā vai dilstošā secībā. Šis solis ir būtisks kvantitu precīzai aprēķināšanai.
- Izvēlieties teorētisko sadalījumu : nosakiet teorētisko sadalījumu, ar kuru vēlaties salīdzināt savu datu kopu. Izplatītas izvēles iespējas ietver parasto sadalījumu, eksponenciālo sadalījumu vai jebkuru citu sadalījumu, kas labi atbilst jūsu datiem.
- Aprēķināt teorētiskās kvantītes : Aprēķiniet kvantiles izvēlētajam teorētiskajam sadalījumam. Piemēram, ja jūs salīdzināt ar normālu sadalījumu, lai atrastu paredzamās kvantiles, izmantojiet normālā sadalījuma apgrieztā kumulatīvā sadalījuma funkciju (CDF).
- Plotēšana :
- Atzīmējiet sakārtotās datu kopas vērtības uz x ass.
- Atzīmējiet atbilstošās teorētiskās kvantiles uz y ass.
- Katrs datu punkts (x, y) apzīmē novēroto un paredzamo vērtību pāri.
- Savienojiet datu punktus, lai vizuāli pārbaudītu saistību starp datu kopu un teorētisko sadalījumu.
Q-Q diagrammas interpretācija
- Ja diagrammas punkti atrodas aptuveni pa taisnu līniju, tas liecina, ka jūsu datu kopa atbilst pieņemtajam sadalījumam.
- Novirzes no taisnās līnijas norāda uz novirzēm no pieņemtā sadalījuma, kas prasa turpmāku izmeklēšanu.
Izplatības līdzības izpēte, izmantojot Q-Q diagrammas
Sadalījuma līdzības izpēte, izmantojot Q-Q diagrammas, ir statistikas pamatuzdevums. Divu datu kopu salīdzināšana, lai noteiktu, vai to izcelsme ir viena un tā pati izplatīšana, ir ļoti svarīga dažādiem analītiskiem nolūkiem. Ja pastāv pieņēmums par kopīgu sadalījumu, datu kopu apvienošana var uzlabot parametru novērtējuma precizitāti, piemēram, attiecībā uz atrašanās vietu un mērogu. Q-Q diagrammas, saīsinājums no kvantiļu-kvantiļu diagrammas, piedāvā vizuālu metodi sadalījuma līdzības novērtēšanai. Šajos diagrammās vienas datu kopas kvantiles tiek attēlotas pret citas datu kopas kvantilēm. Ja punkti cieši sakrīt pa diagonālo līniju, tas liecina par sadalījumu līdzību. Novirzes no šīs diagonālās līnijas norāda uz atšķirībām sadalījuma raksturlielumos.
Kamēr tādi testi kā chi kvadrāts un Kolmogorovs-Smirnovs testi var novērtēt vispārējās sadalījuma atšķirības, Q-Q diagrammas nodrošina niansētu perspektīvu, tieši salīdzinot kvantiles. Tas ļauj analītiķiem saskatīt konkrētas atšķirības, piemēram, izmaiņas atrašanās vietā vai mēroga izmaiņas, kuras var nebūt redzamas tikai no formāliem statistikas testiem.
Q-Q diagrammas Python ieviešana
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
Izvade:
Q-Q sižets
Šeit, tā kā datu punkti aptuveni seko taisnai līnijai Q-Q diagrammā, tas liecina, ka datu kopa atbilst pieņemtajam teorētiskajam sadalījumam, ko šajā gadījumā mēs uzskatījām par normālu sadalījumu.
Q-Q sižeta priekšrocības
- Elastīgs salīdzinājums : Q-Q diagrammas var salīdzināt dažāda lieluma datu kopas bez nepieciešami vienādi paraugu izmēri.
- Bezdimensiju analīze : tiem nav izmēru, tāpēc tie ir piemēroti datu kopu salīdzināšanai ar dažādas mērvienības vai skalas.
- Vizuālā interpretācija : nodrošina skaidru vizuālu datu sadalījuma attēlojumu salīdzinājumā ar teorētisko sadalījumu.
- Jutīgs pret novirzēm : viegli nosaka novirzes no pieņemtajiem sadalījumiem, palīdzot identificēt datu neatbilstības.
- Diagnostikas rīks : palīdz novērtēt sadalījuma pieņēmumus, identificēt novirzes un izprast datu modeļus.
Kvantiļu-kvantiļu diagrammas pielietojumi
Kvantiles-kvantiles diagrammu izmanto šādiem mērķiem:
- Sadales pieņēmumu novērtēšana : Q-Q diagrammas bieži tiek izmantotas, lai vizuāli pārbaudītu, vai datu kopa atbilst noteiktam varbūtības sadalījumam, piemēram, normālajam sadalījumam. Salīdzinot novēroto datu kvantiles ar pieņemtā sadalījuma kvantilēm, var konstatēt novirzes no pieņemtā sadalījuma. Tas ir ļoti svarīgi daudzās statistikas analīzēs, kur sadalījuma pieņēmumu derīgums ietekmē statistisko secinājumu precizitāti.
- Noviržu noteikšana : izņēmumi ir datu punkti, kas ievērojami atšķiras no pārējās datu kopas. Q-Q diagrammas var palīdzēt identificēt novirzes, atklājot datu punktus, kas ir tālu no paredzamā sadalījuma modeļa. Ārpuses var parādīties kā punkti, kas novirzās no paredzamās taisnes diagrammā.
- Izplatījumu salīdzināšana : Q-Q diagrammas var izmantot, lai salīdzinātu divas datu kopas, lai noskaidrotu, vai tās nāk no viena sadalījuma. Tas tiek panākts, attēlojot vienas datu kopas kvantiles pret citas datu kopas kvantilēm. Ja punkti atrodas aptuveni pa taisnu līniju, tas liecina, ka abas datu kopas ir iegūtas no viena sadalījuma.
- Normalitātes novērtēšana : Q-Q diagrammas ir īpaši noderīgas datu kopas normalitātes novērtēšanai. Ja datu punkti diagrammā cieši seko taisnai līnijai, tas norāda, ka datu kopa ir aptuveni normāli izplatīta. Atkāpes no līnijas liecina par novirzēm no normas, kas var prasīt papildu izmeklēšanu vai neparametriskas statistikas metodes.
- Modeļa apstiprināšana : tādās jomās kā ekonometrija un mašīnmācība Q-Q diagrammas tiek izmantotas, lai apstiprinātu prognozēšanas modeļus. Salīdzinot novēroto atbilžu kvantiles ar modeļa prognozētajām kvantilēm, var novērtēt, cik labi modelis atbilst datiem. Novirzes no paredzamā modeļa var norādīt uz jomām, kurās modelim ir nepieciešami uzlabojumi.
- Kvalitātes kontrole : Q-Q diagrammas tiek izmantotas kvalitātes kontroles procesos, lai uzraudzītu izmērīto vai novēroto vērtību sadalījumu laikā vai dažādās partijās. Atkāpes no paredzamajiem modeļiem diagrammā var liecināt par izmaiņām pamatā esošajos procesos, mudinot veikt turpmāku izmeklēšanu.
Q-Q diagrammu veidi
Pastāv vairāki Q-Q diagrammu veidi, ko parasti izmanto statistikā un datu analīzē, un katrs ir piemērots dažādiem scenārijiem vai mērķiem:
- Normāls sadalījums : simetrisks sadalījums, kurā Q-Q diagramma parādītu punktus aptuveni pa diagonālo līniju, ja dati atbilst normālam sadalījumam.
- Pa labi šķībs sadalījums : sadalījums, kurā Q-Q diagramma parādītu modeli, kurā novērotās kvantiles novirzās no taisnās līnijas virzienā uz augšējo galu, norādot uz garāku asti labajā pusē.
- Pa kreisi šķībs sadalījums : sadalījums, kurā Q-Q diagramma parādītu modeli, kurā novērotās kvantiles novirzās no taisnās līnijas uz apakšējo galu, norādot uz garāku asti kreisajā pusē.
- Nepietiekami izkliedēta izplatīšana : sadalījums, kurā Q-Q diagrammā novērotās kvantiles būtu redzamas ciešāk ap diagonālo līniju, salīdzinot ar teorētiskajām kvantilēm, kas liecina par mazāku dispersiju.
- Pārāk izkliedēta izplatīšana : sadalījums, kurā Q-Q diagrammā novērotās kvantiles būtu vairāk izkliedētas vai novirzes no diagonālās līnijas, kas norāda uz lielāku dispersiju vai izkliedi, salīdzinot ar teorētisko sadalījumu.
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
Izvade:
Q-Q grafiks dažādiem sadalījumiem
rādītājs c
