Ņūtona dzesēšanas likums ir pamatlikums, kas raksturo siltuma pārneses ātrumu no ķermeņa uz apkārtējo starojumu. Šis likums nosaka, ka ātrums, ar kādu ķermenis izstaro siltumu, ir tieši proporcionāls ķermeņa temperatūras starpībai no apkārtējās vides, ņemot vērā, ka temperatūras starpība ir zema. t.i., jo lielāka ir atšķirība starp ķermeņa un tā apkārtnes temperatūru, jo vairāk siltuma tiek zaudēts un jo zemāka temperatūra, jo mazāk siltuma tiek zaudēts. Ņūtona dzesēšanas likums ir īpašs Stefana-Bolcmaņa likuma gadījums.

Šajā rakstā mēs sīkāk uzzināsim par Ņūtona dzesēšanas likumu, Ņūtona dzesēšanas formulas likumu, tā atvasinājumu, piemēriem un citiem.

Ņūtona dzesēšanas likuma definīcija

Ņūtons bija pirmais, kurš pētīja attiecības starp ķermeņa zaudēto siltumu apkārtējai videi. Viņš norāda, ka jo lielāka temperatūras atšķirība starp objektu un tā apkārtni, jo vairāk siltuma izstaro ķermenis.

Ņūtona dzesēšanas likums nosaka, ka

Siltuma zuduma ātrums no ķermeņa ir tieši proporcionāls temperatūras starpībai starp ķermeni un tā apkārtni, ņemot vērā, ka temperatūras starpība nav liela.

Šis likums tiek izmantots, lai izskaidrotu, kāpēc karsts ūdens vai uz galda atstāts piens atdziest ātrāk nekā nedaudz silta piena vai ūdens, kas palicis uz galda. Ņūtona dzesēšanas likums palīdz mums noteikt jebkura cilvēka temperatūru, to faktiski neizmērot, ņemot vērā ķermeņa sākotnējo temperatūru un apkārtējās vides temperatūru.

Ņūtona dzesēšanas formulas likums

Ņūtona dzesēšanas formulas likums ir formula materiāla temperatūras aprēķināšanai, jo tas starojuma rezultātā zaudē siltumu apkārtējai videi.

Saskaņā ar Ņūtona dzesēšanas likumu,

Siltuma zuduma ātrums ( – dQ/dt) ķermeņa temperatūra ir tieši proporcionāla temperatūras starpībai [ΔT = (T ₂ – T ₁ )] ķermeni un apkārtni.

kas ir svn checkout

Mēs varam to pārstāvēt kā

– dQ/dt ∝ (T ₂ – T ₁ )

– dQ/dt = k(T ₂ – T ₁ )

kur,
k ir proporcionalitātes konstante

Atrisinot iepriekš minēto diferenciālvienādojumu, mēs iegūstam,

T(t) = T _s + (T _O – T _s ) Tas ir ^-kt

kur,
t ir laiks
T(t) ir Ķermeņa temperatūra laikā t
T _s ir apkārtējā temperatūra
T _O ir ķermeņa sākotnējā temperatūra
k ir proporcionalitātes konstante

Ņūtona dzesēšanas likuma atvasinājums

Ņūtona dzesēšanas likuma formulu var iegūt, izmantojot diferenciālvienādojuma risinājumu. Ļaujiet ķermenim ar masu m ar īpatnējo siltumietilpību s atrasties temperatūrā T₂un T₁ir apkārtējās vides temperatūra.

Ja temperatūra nedaudz pazeminās dT ₂ laikā dt , tad zaudētais siltuma daudzums ir,

dQ = ms dT ₂

Siltuma zuduma ātrumu nosaka,

dQ/dt = ms (dT ₂ /dt)

Saskaņā ar Ņūtona dzesēšanas likumu,

– dQ/dt = k(T ₂ – T ₁ )

Salīdzinot iepriekš minēto vienādojumu

– ms (dT ₂ /dt) = k (T ₂ – T ₁ )

dT ₂ /(T ₂ – T ₁ ) = – (k / ms) dt

dT ₂ /(T ₂ – T ₁ ) = – Kdt

kur, K = k/m s

Iepriekš minētā vienādojuma integrēšana

žurnāls _{Tas ir} (T ₂ – T ₁ ) = – K t + c

T ₂ = T ₁ + C’ un ^–Kt

kur, C' = e ^c

Sakarība starp ķermeņa temperatūras kritumu un laiku tiek parādīta, izmantojot dzesēšanas grafiku. Šī grafika slīpums parāda temperatūras krituma ātrumu.

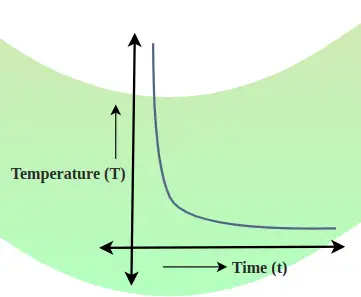
Dzesēšanas līkne ir grafiks, kas parāda saistību starp ķermeņa temperatūru un laiku. Temperatūras krituma ātrumu nosaka līknes pieskares slīpums jebkurā punktā. Tālāk pievienotajā attēlā parādīta temperatūras krituma un laika attiecība.

Kopumā

T(t) = T _A +(T _H -T _A )Tas ir ^-kt

kur
T(t) ir temperatūra laikā t
T _A ir apkārtējās vides temperatūra vai temperatūra
T _H ir karstā objekta temperatūra
k ir pozitīvā konstante un t ir laiks

Metodes, kā piemērot Ņūtona dzesēšanas likumu

Pie nemainīga dzesēšanas ātruma dzesēšanas ātrums ir saistīts ar ķermeņa vidējo temperatūru intervālā, pēc tam mēs varam aprēķināt aptuveno vērtību, izmantojot Ņūtona dzesēšanas likumu

dθ/dt = k(q – q _s )

kur,
q ir ķermeņa temperatūra
q _s ir apkārtējās vides temperatūra

Tagad, ja ķermeņa vidējā temperatūra ir q, kur,

q = (q _i + q _f )/2

Ņūtona dzesēšanas likuma pārbaude

Mēs varam viegli pārbaudīt Ņūtona dzesēšanas likumu, izmantojot tālāk aprakstīto eksperimentu:

pārvērst veselu skaitli par virkni java

Eksperimentā mēs ņemam dubultsienu trauku (V) ar ūdeni starp abām sienām. Dubultsienu trauka iekšpusē mēs ņemam vara kalorimetru (C), kas satur karstu ūdeni.

Mēs izmantojam divus termometrus T₂lai izmērītu ūdens temperatūru kalorimetrā un T₁lai izmērītu temperatūru karstā ūdens starp dubultsienām. Pēc vienādiem laika intervāliem tiek atzīmētas abas temperatūras un grafiks starp žurnālu_{Tas ir}(T₂– T₁) un laiks (t), kas parādās kā taisna līnija ar negatīvu slīpumu.

Ņūtona dzesēšanas likuma grafiks

Zemāk ir pievienots Ņūtona dzesēšanas likuma grafiks, šajā grafikā ir parādīts abu temperatūru un laika starpības žurnāls.

Ņūtona dzesēšanas likuma ierobežojumi

Dažādi Ņūtona dzesēšanas likuma ierobežojumi ir:

• Ņūtona dzesēšanas likums ir spēkā, ja temperatūras starpība starp ķermeni un vidi ir neliela.
• Ķermeņa siltuma zudumi ir tikai formā Radiācija .
• Ķermeņa atdzišanas laikā apkārtējās vides temperatūrai jāpaliek nemainīgai, ja ne, tad Ņūtona dzesēšanas likums nepastāv.

Ņūtona dzesēšanas likuma pielietojumi

Dažādi Ņūtona dzesēšanas likuma pielietojumi ir:

• Lai novērtētu, cik ilgi silts priekšmets atdziest līdz noteiktai temperatūrai.
• Lai noteiktu dzēriena temperatūru ledusskapī pēc noteikta laika.
• Tas palīdz norādīt nāves laiku, aplūkojot iespējamo ķermeņa temperatūru nāves brīdī un pašreizējo ķermeņa temperatūru.

Lasīt vairāk,

• Īpatnējā siltuma jauda
• Termodinamikas pamatjēdziens
• Termodinamiskie procesi

Atrisinātie piemēri Ņūtona dzesēšanas likums

1. piemērs. Panna, kas pildīta ar karstu ēdienu, atdziest no 94 °C līdz 86 °C 2 minūtēs, ja istabas temperatūra ir 20 °C. Cik ilgs laiks būs nepieciešams, lai atdzesētu no 71 °C līdz 69 °C?

Risinājums:

Vidējā temperatūra 94 °C un 86 °C ir 90 °C,

• T₂= 90 °C
• T₁= 20 °C

Ieliec tem. ēdiena temperatūra 2 minūtēs ir 8 °C.

Saskaņā ar Ņūtona dzesēšanas likumu,

– dQ/dt = k(T ₂ – T ₁ )

8 °C /2 min = k(90–20)

4 = k(70) ……… (1)

Vidējā temperatūra 69 °C un 71 °C ir 70 °C

• T₂= 70 °C
• T₁= 20 °C

Saskaņā ar Ņūtona dzesēšanas likumu,

2 °C/dt = k(70–20) ……(2)

No (1) un (2) vienādojuma

Laika maiņa = 0,7 min = =42 sek

Tādējādi ēdiena atdzišana no 71 °C līdz 69 °C prasīs 42 sekundes.

2. piemērs. Ķermenis 40ºC temperatūrā tiek turēts vidē ar nemainīgu 20ºC temperatūru. Tiek novērots, ka tā temperatūra nokrītas līdz 35ºC 10 minūtēs. Noskaidrojiet, cik daudz vairāk laika būs nepieciešams, lai ķermenis sasniegtu 30ºC temperatūru.

Risinājums:

Ņemot vērā,

vilks vai lapsa

• q_i= (40 – 20)ºC
• q_f= (35 – 20)ºC

Saskaņā ar Ņūtona dzesēšanas likumu

q _f = q _i Tas ir ^-kt

Tagad par intervālu, kurā temperatūra nokrītas no 40 ºC līdz 35 ºC.

(35 – 20) = (40 – 20) un^-(10k)

Tas ir^-10k= 3/4

-10k = (ln 4/3)

k = 0,2876/10

k = 0,02876

pārbaudiet, vai java nav nulles

Tagad atkal izmantojot Ņūtona formulu,

(30–20) = (35–20)e^-kt

10 = 15e^-kt

Tas ir^-kt= 23

-kt = ln(2/3)

t = 0,40546/k

Izmantojot k vērtību,

t = 0,40546/0,02876

t = 14,098 min

Tādējādi laiks, kas nepieciešams ķermenim, lai sasniegtu 30ºC temperatūru, ir 14,098 minūtes

3. piemērs. Eļļu uzkarsē līdz 70 ºC. Pēc 6 minūtēm tas atdziest līdz 50 ºC. Aprēķiniet laiku, kas vajadzīgs, lai eļļa atdziest no 50 °C līdz 40 °C, ņemot vērā apkārtējo temperatūru T _s = 25 ºC

Risinājums:

Ņemot vērā,

Eļļas temperatūra pēc 6 minūtēm, t.i., T(t) ir 50 ºC

• Apkārtējā temperatūra T_s= 25 ºC
• Eļļas temperatūra, T_O= 70 ºC
• Laiks atdzesēšanai līdz 50ºC = 6 min

Saskaņā ar Ņūtona dzesēšanas likumu,

T(t) = T_s+ (T₀– T_s) Tas ir^-kt

{T(t) – T_s}/(T_O– T_s) = un^-kt

-kt = ln[(T(t) – T_s)/(T_O– T_s)] ………(1)

Aizstājiet vērtības

-kt = ln[(50-25)/(70-25)]

-k = (ln 0,55556)/6

k = 0,09796

Vidējā temperatūra no 50 ºC līdz 40 ºC ir vienāda ar 45 ºC

Atkal izmantojot Ņūtona dzesēšanas likumu

-(0,09796)t = ln[(45–25)/(70–25)]

-0,09796t = ln(0,44444)

0,09796t = 0,81093

t = 0,09796/0,58778 = 8,278 min

Tādējādi laiks, kas nepieciešams eļļai, lai tā atdziest no 50 ºC līdz 40 ºC, ir 8,278 min

4. piemērs: ūdeni karsē līdz 80 ºC 10 minūtes. Cik liela būtu tā temperatūra Celsija grādos, ja k = 0,056 minūtē un apkārtējā temperatūra ir 25 ºC?

Risinājums:

java kārtošanas masīvu saraksts

Ņemot vērā,

• Apkārtējā temperatūra T_s= 25 ºC
• Ūdens temperatūra T₀= 80 ºC
• Ūdens sildīšanas laiks (t) = 10 min
• Konstantes vērtība k = 0,056.

Saskaņā ar Ņūtona dzesēšanas likumu,

T(t) = T_s+ (T₀– T_s) Tas ir^-kt

Vērtības aizstāšana

T(t)= 25 + (80 – 25)e^{(0,056 × 10)}

T(t) = 25 + 55 e^{(0,056 × 10)}

T(t) = 25 + 31,42

T(t) = 56,42

Pēc 10 minūtēm ūdens temperatūra būs 56,42 ºC.

Bieži uzdotie jautājumi par Ņūtona dzesēšanas likumu

Q1: Kas ir Ņūtona dzesēšanas likums?

Atbilde:

Ņūtona dzesēšanas likums nosaka, ka ķermeņa siltuma zudumu ātrums ir tieši proporcionāls temperatūras starpībai starp ķermeni un tā apkārtni.

Q2: Kas ir Ņūtona dzesēšanas formulas likums?

Atbilde:

Ņūtona dzesēšanas likuma formula nosaka, ka

T(t) = T _s + (T _O – T _s ) Tas ir ^-kt

Q3: Kas ir k Ņūtona dzesēšanas likumā?

Atbilde:

The k Ņūtona dzesēšanas likumā formula ir konstante, kas ir atkarīga no materiāla, t.i., mainot materiālu, mainās k Ņūtona dzesēšanas likumā.

Q4: Kāpēc karsto pienu ir vieglāk dzert no trauka nekā no glāzes?

Atbilde:

Bļodiņai ir lielāks virsmas laukums nekā stiklam, tāpēc vairāk siltuma zaudē apkārtnei siltuma starojuma veidā caur bļodu un tādējādi mums ir vieglāk no bļodas izdzert karstu pienu.