Ciparu attēlošanai var izmantot septiņu segmentu displeju. Ņemot vērā masīvu n naturālie skaitļi. Uzdevums ir atrast masīvā skaitli, kas izmanto minimālo segmentu skaitu, lai parādītu skaitli. Ja vairākiem skaitļiem ir minimālais segmentu skaits, tiek izvadīts skaitlis ar mazāko indeksu.
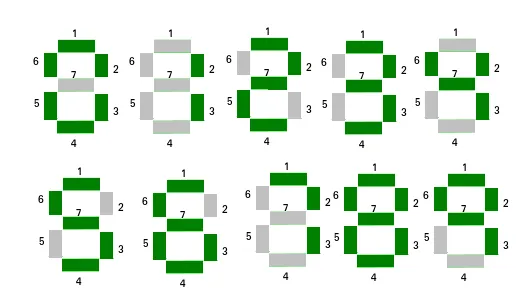
Piemēri:
Ievade: arr[] = { 1 2 3 4 5 }.
Izvade: 1
Paskaidrojums: Elements, kas izmanto minimālo segmentu skaitu, ir 1 (t.i., 2 segmenti)Ievade: arr[] = { 489 206 745 123 756 }.
Izvade: 745
Paskaidrojums: Elements ar mazāko indeksu, kas izmanto minimālo segmentu skaitu, ir 745 (t.i., 12 segmenti)
Ideja ir iepriekš aprēķināt segmentu skaitu, ko izmanto cipari no 0 līdz 9, un saglabāt to. Tagad katram masīva elementam saskaitiet segmenta skaitu, ko izmanto katrs cipars. Pēc tam atrodiet elementu, kas izmanto minimālo segmentu skaitu.
C++Segmenta skaits, ko izmanto cipars:
0 -> 6
1 -> 2
2 -> 5
3 -> 5
4 -> 4
5 -> 5
6 -> 6
7 -> 3
8 -> 7
9 -> 6
#include
import java.io.*; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int []seg = { 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) { if (x == 0) return seg[0]; int count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x /= 10; } return count; } static int elementMinSegment(int []arr int n) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment(arr[0]); int minindex = 0; // Finding and comparing segment used // by each number arr[i]. for (int i = 1; i < n; i++) { int temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } static public void main (String[] args) { int []arr = {489 206 745 123 756}; int n = arr.length; System.out.println(elementMinSegment(arr n)); } }
# Precomputed values of segment # used by digit 0 to 9. seg = [6 2 5 5 4 5 6 3 7 6] # Return the number of # segments used by x. def computeSegment(x): if(x == 0): return seg[0] count = 0 # Finding sum of the segment # used by each digit of a number. while(x): count += seg[x % 10] x = x // 10 return count # function to return minimum sum index def elementMinSegment(arr n): # Initialising the minimum # segment and minimum number index. minseg = computeSegment(arr[0]) minindex = 0 # Finding and comparing segment # used by each number arr[i]. for i in range(1 n): temp = computeSegment(arr[i]) # If arr[i] used less segment # then update minimum segment # and minimum number. if(temp < minseg): minseg = temp minindex = i return arr[minindex] # Driver Code arr = [489 206 745 123 756] n = len(arr) # function print required answer print(elementMinSegment(arr n)) # This code is contributed by # Sanjit_Prasad
using System; class GFG{ // Precomputed values of segment // used by digit 0 to 9. static int []seg = new int[10]{ 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) { if (x == 0) return seg[0]; int count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x /= 10; } return count; } static int elementMinSegment(int []arr int n) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment(arr[0]); int minindex = 0; // Finding and comparing segment used // by each number arr[i]. for (int i = 1; i < n; i++) { int temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } static public void Main() { int []arr = {489 206 745 123 756}; int n = arr.Length; Console.WriteLine(elementMinSegment(arr n)); } }
// Precomputed values of segment // used by digit 0 to 9. let seg = [ 6 2 5 5 4 5 6 3 7 6]; // Return the number of segments used by x. function computeSegment(x) { if (x == 0) return seg[0]; let count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x = parseInt(x / 10 10); } return count; } function elementMinSegment(arr n) { // Initialising the minimum segment // and minimum number index. let minseg = computeSegment(arr[0]); let minindex = 0; // Finding and comparing segment used // by each number arr[i]. for(let i = 1; i < n; i++) { let temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } // Driver code let arr = [ 489 206 745 123 756 ]; let n = arr.length; console.log(elementMinSegment(arr n));
Izvade
745
Laika sarežģītība: O(n * log 10 n)
Palīgtelpa: O(10)
