Luhn algoritms, kas pazīstams arī kā modulis 10 vai pret 10 algoritms ir vienkārša kontrolsummas formula, ko izmanto, lai apstiprinātu dažādus identifikācijas numurus, piemēram, kredītkaršu numurus, IMEI numurus, Kanādas sociālās apdrošināšanas numurus. LUHN formulu 60. gadu beigās izveidoja matemātiķu grupa. Drīz pēc tam kredītkaršu uzņēmumi to pieņēma. Tā kā algoritms ir publiski pieejams, to var izmantot ikviens. Lielākajā daļā kredītkaršu un daudzu valsts identifikācijas numuru algoritms tiek izmantots kā vienkārša metode derīgu numuru atšķiršanai no nepareizi ievadītiem vai citādi nepareiziem numuriem. Tas bija paredzēts, lai aizsargātu pret nejaušām kļūdām, nevis ļaunprātīgiem uzbrukumiem.
Luhn algoritmā iesaistītie soļi
Izpratīsim algoritmu ar piemēru:
Apsveriet konta numura piemēru 79927398713 .
1. darbība – sākot no galējā labā cipara, dubultojiet katra otrā cipara vērtību,
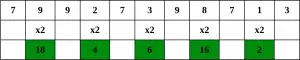
2. darbība – Ja skaitļa dubultošana rada divciparu skaitli, t.i., lielāku par 9 (piemēram, 6 × 2 = 12), pievienojiet reizinājuma ciparus (piemēram, 12: 1 + 2 = 3, 15: 1 + 5 = 6), lai iegūtu viencipara skaitli.

3. darbība – Tagad saskaitiet visu ciparu summu.
saistītais saraksts

4. darbība – Ja kopējais modulo 10 ir vienāds ar 0 (ja summa beidzas ar nulli), tad skaitlis ir derīgs pēc Luna formulas; citādi tas nav derīgs.

Tā kā summa ir 70, kas ir 10 reizinājums, konta numurs, iespējams, ir derīgs.
Ideja ir vienkārša; mēs šķērsojam no beigām. Katram otrajam ciparam pirms pievienošanas mēs to dubultojam. Mēs pievienojam divus ciparus no skaitļa, kas iegūts pēc dubultošanas.
Īstenošana:
C++
// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(>const> string& cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum = 0, isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--) {> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits after> >// doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> >string cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >printf>(>'This is a valid card'>);> >else> >printf>(>'This is not a valid card'>);> >return> 0;> }> |
>
>
Java
// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum =>0>;> >boolean> isSecond =>false>;> >for> (>int> i = nDigits ->1>; i>=>0>; i--)> >{> >int> d = cardNo.charAt(i) ->'0'>;> >if> (isSecond ==>true>)> >d = d *>2>;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d />10>;> >nSum += d %>10>;> >isSecond = !isSecond;> >}> >return> (nSum %>10> ==>0>);> }> >// Driver code> >static> public> void> main (String[] args)> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >System.out.println(>'This is a valid card'>);> >else> >System.out.println(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
java hello programma
>
>
Python3
# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > >nDigits>=> len>(cardNo)> >nSum>=> 0> >isSecond>=> False> > >for> i>in> range>(nDigits>-> 1>,>->1>,>->1>):> >d>=> ord>(cardNo[i])>-> ord>(>'0'>)> > >if> (isSecond>=>=> True>):> >d>=> d>*> 2> > ># We add two digits to handle> ># cases that make two digits after> ># doubling> >nSum>+>=> d>/>/> 10> >nSum>+>=> d>%> 10> > >isSecond>=> not> isSecond> > >if> (nSum>%> 10> =>=> 0>):> >return> True> >else>:> >return> False> # Driver code> if> __name__>=>=>'__main__'>:> > >cardNo>=> '79927398713'> > >if> (checkLuhn(cardNo)):> >print>(>'This is a valid card'>)> >else>:> >print>(>'This is not a valid card'>)> # This code is contributed by rutvik_56> |
>
>
C#
a-b atzarošana
// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.Length;> >int> nSum = 0;> >bool> isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--)>> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> >// Driver code> >static> public> void> Main()> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >Console.WriteLine(>'This is a valid card'>);> >else> >Console.WriteLine(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
>
>
dubultā java
Javascript
> >// Javascript program to implement Luhn algorithm> > >// Returns true if given> >// card number is valid> >function> checkLuhn(cardNo)> >{> >let nDigits = cardNo.length;> >let nSum = 0;> >let isSecond =>false>;> >for> (let i = nDigits - 1; i>= 0; i--)> >{> >let d = cardNo[i].charCodeAt() ->'0'>.charCodeAt();> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += parseInt(d / 10, 10);> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> >}> > >let cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >document.write(>'This is a valid card'>);> >else> >document.write(>'This is not a valid card'>);> > > |
>
>Izvade
This is a valid card>
Luhn algoritms nosaka jebkuru viencipara kļūdu, kā arī gandrīz visas blakus esošo ciparu transponēšanas.
