ZEMĀKAIS KOPĪGAIS PRIEKŠTECIS BINĀRAJĀ KOKĀ

Kas ir zemākais kopīgais priekštecis binārajā kokā?

The zemākais kopīgais sencis ir zemākais mezgls kokā, kuram ir gan n1, gan n2 as pēcnācēji, kur n1 un n2 ir mezgli, kuriem mēs vēlamies atrast LCA. Tādējādi binārā koka ar mezgliem n1 un n2 LCA ir n1 un n2 kopīgais priekštecis, kas atrodas vistālāk no saknes.

Zemākā kopīgā priekšteča (LCA) pielietojums:

Lai noteiktu attālumu starp mezglu pāriem kokā: attālumu no n1 līdz n2 var aprēķināt kā attālumu no saknes līdz n1, plus attālumu no saknes līdz n2, mīnus divreiz attālumu no saknes līdz to zemākajam kopējam. sencis.

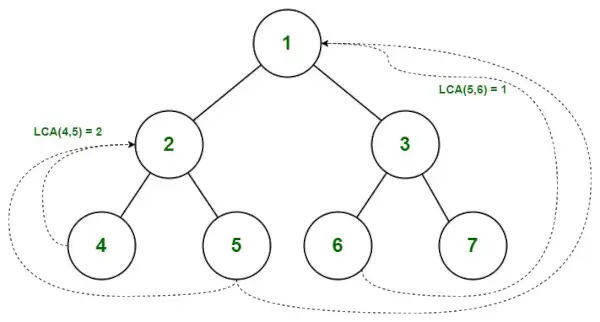
Zemākais kopīgais priekštecis binārajā kokā

Ieteicamā prakse Zemākais izplatītais priekštecis binārajā kokā Izmēģiniet to!

Zemākais kopīgais priekštecis binārajā kokā, saglabājot ceļus no saknes līdz n1 un saknes līdz n2:

Šīs pieejas ideja ir saglabāt ceļu no saknes līdz n1 un saknes uz n2 divās atsevišķās datu struktūrās. Pēc tam vienlaikus apskatiet datu struktūrā saglabātās vērtības un meklējiet pirmo neatbilstību.

Ilustrācija:

Atrodiet 5 un 6 LCA

Ceļš no saknes līdz 5 = { 1, 2, 5 }
Ceļš no saknes līdz 6 = { 1, 3, 6 }

Mēs sākam pārbaudīt no 0 indeksa. Tā kā abas vērtības sakrīt (pathA[0] = pathB[0] ), mēs pārietam uz nākamo indeksu.

pathA[1] nav vienāds ar pathB[1], pastāv neatbilstība, tāpēc mēs ņemam vērā iepriekšējo vērtību.

Tāpēc (5,6) LCA = 1

Lai atrisinātu problēmu, veiciet tālāk norādītās darbības.

Atrodiet ceļu no saknes līdz n1 un saglabājiet to vektorā vai masīvā.
Atrodiet ceļu no saknes līdz n2 un saglabājiet to citā vektorā vai masīvā.
Pārejiet abus ceļus, līdz vērtības masīvos ir vienādas. Atgrieziet kopējo elementu tieši pirms neatbilstības.

Iepriekš minētā algoritma ieviešana ir šāda:

C++

// C++ Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> #include> using> namespace> std;> // A Binary Tree node> struct> Node {> >int> key;> >struct> Node *left, *right;> };> // Utility function creates a new binary tree node with> // given key> Node* newNode(>int> k)> {> >Node* temp =>new> Node;> >temp->taustiņš = k;> >temp->pa kreisi = temp->right = NULL;> >return> temp;> }> // Finds the path from root node to given root of the tree,> // Stores the path in a vector path[], returns true if path> // exists otherwise false> bool> findPath(Node* root, vector<>int>>& ceļš,>int> k)> (root->pa labi && atrastPath(sakne->pa labi, ceļš, k)))> >return> true>;> >// If not present in subtree rooted with root, remove> >// root from path[] and return false> >path.pop_back();> >return> false>;> > // Returns LCA if node n1, n2 are present in the given> // binary tree, otherwise return -1> int> findLCA(Node* root,>int> n1,>int> n2)> > // Driver program to test above functions> int> main()> {> >// Let us create the Binary Tree shown in above diagram.> >Node* root = newNode(1);> >root->pa kreisi = newNode(2);> >root->pa labi = newNode(3);> >root->pa kreisi->pa kreisi = newNode(4);> >root->pa kreisi->pa labi = newNode(5);> >root->pa labi-> pa kreisi = newNode(6);> >root->pa labi->pa labi = newNode(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5);> >cout <<>

'
LCA(4, 6) = '>

<< findLCA(root, 4, 6);> >cout <<>

'
LCA(3, 4) = '>

<< findLCA(root, 3, 4);> >cout <<>

'
LCA(2, 4) = '>

<< findLCA(root, 2, 4);> >return> 0;> }>

Java

// Java Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA of> // two given values n1 and n2> import> java.util.ArrayList;> import> java.util.List;> // A Binary Tree node> class> Node {> >int> data;> >Node left, right;> >Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> List path1 =>new> ArrayList();> >private> List path2 =>new> ArrayList();> >// Finds the path from root node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.clear();> >path2.clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >System.out.println((path1.size()>>>)> >?>'n1 is present'> >:>'n1 is missing'>);> >System.out.println((path2.size()>>>)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> ->1>;> >}> >int> i;> >for> (i =>0>

; i   i++) {  // System.out.println(path1.get(i) + ' ' +  // path2.get(i));  if (!path1.get(i).equals(path2.get(i)))  break;  }  return path1.get(i - 1);  }  // Finds the path from root node to given root of the  // tree, Stores the path in a vector path[], returns  // true if path exists otherwise false  private boolean findPath(Node root, int n,  List path)  {  // base case  if (root == null) {  return false;  }  // Store this node . The node will be removed if  // not in path from root to n.  path.add(root.data);  if (root.data == n ||  findPath(root.left, n, path) ||  findPath(root.right, n, path)) {  return true;  }  // If not present in subtree rooted with root,  // remove root from path[] and return false  path.remove(path.size() - 1);  return false;  }  // Driver code  public static void main(String[] args)  {  BT_NoParentPtr_Solution1 tree  = new BT_NoParentPtr_Solution1();  tree.root = new Node(1);  tree.root.left = new Node(2);  tree.root.right = new Node(3);  tree.root.left.left = new Node(4);  tree.root.left.right = new Node(5);  tree.root.right.left = new Node(6);  tree.root.right.right = new Node(7);  System.out.println('LCA(4, 5) = '  + tree.findLCA(4, 5));  System.out.println('LCA(4, 6) = '  + tree.findLCA(4, 6));  System.out.println('LCA(3, 4) = '  + tree.findLCA(3, 4));  System.out.println('LCA(2, 4) = '  + tree.findLCA(2, 4));  } } // This code is contributed by Sreenivasulu Rayanki.>

Python3

# Python Program for Lowest Common Ancestor in a Binary Tree> # O(n) solution to find LCS of two given values n1 and n2> # A binary tree node> class> Node:> ># Constructor to create a new binary node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # Finds the path from root node to given root of the tree.> # Stores the path in a list path[], returns true if path> # exists otherwise false> def> findPath(root, path, k):> ># Baes Case> >if> root>is> None>:> >return> False> ># Store this node is path vector. The node will be> ># removed if not in path from root to k> >path.append(root.key)> ># See if the k is same as root's key> >if> root.key>=>=> k:> >return> True> ># Check if k is found in left or right sub-tree> >if> ((root.left !>=> None> and> findPath(root.left, path, k))>or> >(root.right !>=> None> and> findPath(root.right, path, k))):> >return> True> ># If not present in subtree rooted with root, remove> ># root from path and return False> >path.pop()> >return> False> # Returns LCA if node n1 , n2 are present in the given> # binary tree otherwise return -1> def> findLCA(root, n1, n2):> ># To store paths to n1 and n2 fromthe root> >path1>=> []> >path2>=> []> ># Find paths from root to n1 and root to n2.> ># If either n1 or n2 is not present , return -1> >if> (>not> findPath(root, path1, n1)>or> not> findPath(root, path2, n2)):> >return> ->1> ># Compare the paths to get the first different value> >i>=> 0> >while>(i <>len>(path1)>and> i <>len>(path2)):> >if> path1[i] !>=> path2[i]:> >break> >i>+>=> 1> >return> path1[i>->1>]> # Driver program to test above function> if> __name__>=>=> '__main__'>:> > ># Let's create the Binary Tree shown in above diagram> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> > >print>(>'LCA(4, 5) = %d'> %> (findLCA(root,>4>,>5>,)))> >print>(>'LCA(4, 6) = %d'> %> (findLCA(root,>4>,>6>)))> >print>(>'LCA(3, 4) = %d'> %> (findLCA(root,>3>,>4>)))> >print>(>'LCA(2, 4) = %d'> %> (findLCA(root,>2>,>4>)))> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// C# Program for Lowest Common> // Ancestor in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> using> System.Collections;> using> System;> // A Binary Tree node> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> ArrayList path1 =>new> ArrayList();> >private> ArrayList path2 =>new> ArrayList();> >// Finds the path from root> >// node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.Clear();> >path2.Clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >Console.Write((path1.Count>0)> >?>'n1 is present'> >:>'n1 is missing'>);> >Console.Write((path2.Count>0)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> -1;> >}> >int> i;> >for>

(i = 0; i   i++) {  // System.out.println(path1.get(i)  // + ' ' + path2.get(i));  if ((int)path1[i] != (int)path2[i])  break;  }  return (int)path1[i - 1];  }  // Finds the path from root node  // to given root of the tree,  // Stores the path in a vector  // path[], returns true if path  // exists otherwise false  private bool findPath(Node root, int n, ArrayList path)  {  // base case  if (root == null) {  return false;  }  // Store this node . The node  // will be removed if not in  // path from root to n.  path.Add(root.data);  if (root.data == n) {  return true;  }  if (root.left != null  && findPath(root.left, n, path)) {  return true;  }  if (root.right != null  && findPath(root.right, n, path)) {  return true;  }  // If not present in subtree  // rooted with root, remove root  // from path[] and return false  path.RemoveAt(path.Count - 1);  return false;  }  // Driver code  public static void Main(String[] args)  {  BT_NoParentPtr_Solution1 tree  = new BT_NoParentPtr_Solution1();  tree.root = new Node(1);  tree.root.left = new Node(2);  tree.root.right = new Node(3);  tree.root.left.left = new Node(4);  tree.root.left.right = new Node(5);  tree.root.right.left = new Node(6);  tree.root.right.right = new Node(7);  Console.Write('LCA(4, 5) = ' + tree.findLCA(4, 5));  Console.Write('
LCA(4, 6) = '  + tree.findLCA(4, 6));  Console.Write('
LCA(3, 4) = '  + tree.findLCA(3, 4));  Console.Write('
LCA(2, 4) = '  + tree.findLCA(2, 4));  } } // This code is contributed by Rutvik_56>

Javascript

> >// JavaScript Program for Lowest Common> >// Ancestor in a Binary Tree> >// A O(n) solution to find LCA of> >// two given values n1 and n2> > >class Node> >{> >constructor(value) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = value;> >}> >}> > >let root;> >let path1 = [];> >let path2 = [];> > >// Finds the path from root node to given root of the tree.> >function> findLCA(n1, n2) {> >path1 = [];> >path2 = [];> >return> findLCAInternal(root, n1, n2);> >}> > >function> findLCAInternal(root, n1, n2) {> > >if> (!findPath(root, n1, path1) || !findPath(root, n2, path2))> >{> >document.write((path1.length>0) ?>> 'n1 is present'> :>'n1 is missing'>);> >document.write((path2.length>0) ?>> 'n2 is present'> :>'n2 is missing'>);> >return> -1;> >}> > >let i;> >for>

(i = 0; i     // System.out.println(path1.get(i) + ' ' + path2.get(i));  if (path1[i] != path2[i])  break;  }    return path1[i-1];  }    // Finds the path from root node to   // given root of the tree, Stores the  // path in a vector path[], returns true  // if path exists otherwise false  function findPath(root, n, path)  {  // base case  if (root == null) {  return false;  }    // Store this node . The node will be removed if  // not in path from root to n.  path.push(root.data);    if (root.data == n) {  return true;  }    if (root.left != null && findPath(root.left, n, path)) {  return true;  }    if (root.right != null && findPath(root.right, n, path)) {  return true;  }    // If not present in subtree rooted with root,   // remove root from  // path[] and return false  path.pop();    return false;  }    root = new Node(1);  root.left = new Node(2);  root.right = new Node(3);  root.left.left = new Node(4);  root.left.right = new Node(5);  root.right.left = new Node(6);  root.right.right = new Node(7);  document.write('LCA(4, 5) = ' + findLCA(4,5) + '');  document.write('LCA(4, 6) = ' + findLCA(4,6) + '');  document.write('LCA(3, 4) = ' + findLCA(3,4) + '');  document.write('LCA(2, 4) = ' + findLCA(2,4));>

Izvade

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>

Laika sarežģītība: O(N). Koks tiek šķērsots divas reizes, un tad tiek salīdzināti ceļu masīvi.
Palīgtelpa: O(N). Papildu vieta path1 un path2.

Zemākais kopīgais priekštecis binārajā kokā, veicot vienu šķērsošanu:

Ideja ir šķērsot koku, sākot no saknes. Ja kāda no dotajām atslēgām (n1 un n2) sakrīt ar sakni, tad sakne ir LCA (pieņemot, ka ir abas atslēgas). Ja sakne nesakrīt ar kādu no taustiņiem, mēs atkārtojam kreiso un labo apakškoku.

Mezgls, kura kreisajā apakškokā ir viena atslēga, bet labajā apakškokā ir otra atslēga, ir LCA.

Ja abas atslēgas atrodas kreisajā apakškokā, tad kreisajā apakškokā ir arī LCA,

Pretējā gadījumā LCA atrodas labajā apakškokā.

Ilustrācija:

Atrodiet 5 un 6 LCA

Sakne norāda uz mezglu ar vērtību 1, jo tā vērtība neatbilst {5, 6}. Mēs meklējam atslēgu kreisajā apakškokā un labajā apakškokā.

Kreisais apakškoks:

Jauna sakne = { 2 } ≠ 5 vai 6, tāpēc mēs turpināsim savu rekursiju

Jauna sakne = {4}, tā kreisā un labā apakškoka vērtība ir nulle, mēs atgriezīsim NULL šim zvanam

Jauna sakne = {5}, vērtība atbilst 5, tāpēc tiks atgriezts mezgls ar vērtību 5

Funkcijas izsaukums root ar vērtību 2 atgriezīs vērtību 5

Labais apakškoks:

Sakne = { 3 } ≠ 5 vai 6, tāpēc mēs turpinām savu rekursiju

Sakne = {6} = 5 vai 6, mēs atgriezīsim šo mezglu ar vērtību 6

Sakne = {7} ≠ 5 vai 6, mēs atgriezīsim NULL

Tātad funkcijas izsaukums root ar vērtību 3 atgriezīs mezglu ar vērtību 6

Tā kā mezgla kreisais apakškoks un labais apakškoks ar vērtību 1 nav NULL, tāpēc 1 ir LCA

Lai atrisinātu problēmu, veiciet tālāk norādītās darbības.

Mēs nododam sakni palīgfunkcijai un pārbaudām, vai saknes vērtība atbilst kādam no n1 un n2.
- Ja JĀ, atgrieziet sakni
- cits rekursīvs izsaukums kreisajā un labajā apakškokā
Būtībā mēs veicam iepriekšēju pasūtīšanu, vispirms pārbaudot, vai saknes->vērtība atbilst n1 vai n2. Pēc tam šķērsojiet kreiso un labo apakškoku.
Ja ir kāda sakne, kas atgriež vienu NULL un citu NONNULL vērtību, mēs atgriežam attiecīgo NON-NULL vērtību šim mezglam.
Mezgls, kas atgriež abas NONNULL vērtības gan kreisajam, gan labajam apakškokam, ir mūsu zemākais kopīgais priekštecis.

Zemāk ir aprakstīta iepriekš minētās pieejas īstenošana.

C++

/* C++ Program to find LCA of n1 and n2 using one traversal> >* of Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->taustiņš = atslēga;> >temp->pa kreisi = temp->right = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> struct> Node* findLCA(>struct> Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->taustiņš == n1> // Driver program to test above functions> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->pa kreisi = newNode(2);> >root->pa labi = newNode(3);> >root->pa kreisi->pa kreisi = newNode(4);> >root->pa kreisi->pa labi = newNode(5);> >root->pa labi-> pa kreisi = newNode(6);> >root->pa labi->pa labi = newNode(7);> >cout <<>'LCA(4, 5) = '>

  cout << '
LCA(4, 6) = '   cout << '
LCA(3, 4) = '   cout << '
LCA(2, 4) = '   return 0; } // This code is contributed by Aditya Kumar (adityakumar129)>

C

// C Program to find LCA of n1 and n2 using one traversalof> // Binary Tree> #include> #include> // A Binary Tree Node> typedef> struct> Node {> >struct> Node *left, *right;> >int> key;> } Node;> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp = (Node*)>malloc>(>sizeof>(Node));> >temp->taustiņš = atslēga;> >temp->pa kreisi = temp->right = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> Node* findLCA(Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->taustiņš == n1> // Driver program to test above functions> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->pa kreisi = newNode(2);> >root->pa labi = newNode(3);> >root->pa kreisi->pa kreisi = newNode(4);> >root->pa kreisi->pa labi = newNode(5);> >root->pa labi->pa kreisi = newNode(6);> >root->pa labi->pa labi = newNode(7);> >printf>(>'LCA(4, 5) = %d'>, findLCA(root, 4, 5)->atslēga);> >printf>(>

'
LCA(4, 6) = %d'>

, findLCA(root, 4, 6)->atslēga);> >printf>(>

'
LCA(3, 4) = %d'>

, findLCA(root, 3, 4)->atslēga);> >printf>(>

'
LCA(2, 4) = %d'>

, findLCA(root, 2, 4)->atslēga);> >return> 0;> }> // This code is contributed by Aditya Kumar (adityakumar129)>

Java

// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> /* Class containing left and right child of current> >node and key value*/> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> >> >// Base case> >if> (node ==>null>)> >return> null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by returning root (Note that> >// if a key is ancestor of other, then the ancestor> >// key becomes LCA> >if> (node.data == n1> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ tree.findLCA(>4>,>5>).data);> >System.out.println(>'LCA(4, 6) = '> >+ tree.findLCA(>4>,>6>).data);> >System.out.println(>'LCA(3, 4) = '> >+ tree.findLCA(>3>,>4>).data);> >System.out.println(>'LCA(2, 4) = '> >+ tree.findLCA(>2>,>4>).data);> >}> }>

Python3

# Python program to find LCA of n1 and n2 using one> # traversal of Binary tree> # A binary tree node> class> Node:> ># Constructor to create a new tree node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function returns pointer to LCA of two given> # values n1 and n2> # This function assumes that n1 and n2 are present in> # Binary Tree> def> findLCA(root, n1, n2):> ># Base Case> >if> root>is> None>:> >return> None> ># If either n1 or n2 matches with root's key, report> ># the presence by returning root (Note that if a key is> ># ancestor of other, then the ancestor key becomes LCA> >if> root.key>=>=> n1>or> root.key>=>=> n2:> >return> root> ># Look for keys in left and right subtrees> >left_lca>=> findLCA(root.left, n1, n2)> >right_lca>=> findLCA(root.right, n1, n2)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> # Driver code> if> __name__>=>=> '__main__'>:> > ># Let us create a binary tree given in the above example> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>).key)> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>).key)> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>).key)> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>).key)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// C# implementation to find lowest common> // ancestor of n1 and n2 using one traversal> // of binary tree> using> System;> // Class containing left and right> // child of current node and key value> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA> >// of two given values n1 and n2. This> >// function assumes that n1 and n2 are> >// present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> > node.data == n2)> >return> node;> >// Look for keys in left and right subtrees> >Node left_lca = findLCA(node.left, n1, n2);> >Node right_lca = findLCA(node.right, n1, n2);> >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree> >// and other is present in other, So this> >// node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or> >// right subtree is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >> >// Driver code> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> >+ tree.findLCA(4, 5).data);> >Console.WriteLine(>'LCA(4, 6) = '> >+ tree.findLCA(4, 6).data);> >Console.WriteLine(>'LCA(3, 4) = '> >+ tree.findLCA(3, 4).data);> >Console.WriteLine(>'LCA(2, 4) = '> >+ tree.findLCA(2, 4).data);> >}> }> // This code is contributed by pratham76>

Javascript

> >// JavaScript implementation to find> >// lowest common ancestor of> >// n1 and n2 using one traversal of binary tree> > >class Node> >{> >constructor(item) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = item;> >}> >}> > >//Root of the Binary Tree> >let root;> > >function> findlCA(n1, n2)> >{> >return> findLCA(root, n1, n2);> >}> > >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >function> findLCA(node, n1, n2)> >> > >root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >document.write(>'LCA(4, 5) = '> +> >findlCA(4, 5).data +>''>);> >document.write(>'LCA(4, 6) = '> +> >findlCA(4, 6).data +>''>);> >document.write(>'LCA(3, 4) = '> +> >findlCA(3, 4).data +>''>);> >document.write(>'LCA(2, 4) = '> +> >findlCA(2, 4).data +>''>);> > >

Izvade

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>

Laika sarežģītība : O(N), jo šī metode veic vienkāršu koka šķērsošanu augšupējā veidā.
Palīgtelpa: O(H), kur H ir koka augstums.

Piezīme: Iepriekš minētā metode paredz, ka atslēgas atrodas Binārajā kokā . Ja viena atslēga ir pieejama, bet otra nav, tā atgriež pašreizējo atslēgu kā LCA (ideālā gadījumā būtu jāatgriež NULL). Mēs varam paplašināt šo metodi, lai apstrādātu visus gadījumus, vispirms pārbaudot, vai kokā ir n1 un n2, un pēc tam atrodot n1 un n2 LCA. Lai pārbaudītu, vai mezgls ir vai nav binārajā kokā, pārejiet pa koku gan n1, gan n2 mezgliem atsevišķi.

C++

/* C++ program to find LCA of n1 and n2 using one traversal> >of Binary Tree. It handles all cases even when n1 or n2> >is not there in Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->taustiņš = atslēga;> >temp->pa kreisi = temp->right = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given> // valuesn1 and n2.> struct> Node* findLCAUtil(>struct> Node* root,>int> n1,>int> n2)> > // Returns true if key k is present in tree rooted with root> bool> find(Node* root,>int> k)> find(root->pa labi, k))> >return> true>;> >// Else return false> >return> false>;> > // This function returns LCA of n1 and n2 only if both n1> // and n2 are present in tree, otherwise returns NULL;> Node* findLCA(Node* root,>int> n1,>int> n2)> {> >// Return LCA only if both n1 and n2 are present in tree> >if> (find(root, n1) and find(root, n2))> >return> findLCAUtil(root, n1, n2);> >// Else return NULL> >return> NULL;> }> // Driver program to test above functions> int> main()> {> >// Let us create a binary tree given in the above> >// example> >Node* root = newNode(1);> >root->pa kreisi = newNode(2);> >root->pa labi = newNode(3);> >root->pa kreisi->pa kreisi = newNode(4);> >root->pa kreisi->pa labi = newNode(5);> >root->pa labi-> pa kreisi = newNode(6);> >root->pa labi->pa labi = newNode(7);> >Node* lca = findLCA(root, 4, 5);> >if> (lca != NULL)> >cout <<>'LCA(4, 5) = '>

  else  cout << 'Keys are not present ';  lca = findLCA(root, 4, 10);  if (lca != NULL)  cout << '
LCA(4, 10) = '   else  cout << '
Keys are not present ';  return 0; } // This code is contributed by Kshitij Dwivedi // (kshitijdwivedi28)>

Java

// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >static> boolean> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >Node findLCAUtil(Node node,>int> n1,>int> n2)> >{> >// Base case> >if> (node ==>null>)> >return> null>;> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>)> >return> temp;> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2)> >return> lca;> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >Node lca = tree.findLCA(>4>,>5>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 5) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >lca = tree.findLCA(>4>,>10>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 10) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >}> }>

Python3

''' Program to find LCA of n1 and n2 using one traversal of> >Binary tree> It handles all cases even when n1 or n2 is not there in tree> '''> # A binary tree node> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function return pointer to LCA of two given values> # n1 and n2> # v1 is set as true by this function if n1 is found> # v2 is set as true by this function if n2 is found> def> findLCAUtil(root, n1, n2, v):> ># Base Case> >if> root>is> None>:> >return> None> ># IF either n1 or n2 matches ith root's key, report> ># the presence by setting v1 or v2 as true and return> ># root (Note that if a key is ancestor of other, then> ># the ancestor key becomes LCA)> >if> root.key>=>=> n1:> >v[>0>]>=> True> >return> root> >if> root.key>=>=> n2:> >v[>1>]>=> True> >return> root> ># Look for keys in left and right subtree> >left_lca>=> findLCAUtil(root.left, n1, n2, v)> >right_lca>=> findLCAUtil(root.right, n1, n2, v)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> def> find(root, k):> ># Base Case> >if> root>is> None>:> >return> False> ># If key is present at root, or if left subtree or right> ># subtree , return true> >if> (root.key>=>=> k>or> find(root.left, k)>or> >find(root.right, k)):> >return> True> ># Else return false> >return> False> # This function returns LCA of n1 and n2 on value if both> # n1 and n2 are present in tree, otherwise returns None> def> findLCA(root, n1, n2):> ># Initialize n1 and n2 as not visited> >v>=> [>False>,>False>]> ># Find lca of n1 and n2 using the technique discussed above> >lca>=> findLCAUtil(root, n1, n2, v)> ># Returns LCA only if both n1 and n2 are present in tree> >if> (v[>0>]>and> v[>1>]>or> v[>0>]>and> find(lca, n2)>or> v[>1>]>and> >find(lca, n1)):> >return> lca> ># Else return None> >return> None> # Driver program to test above function> root>=> Node(>1>)> root.left>=> Node(>2>)> root.right>=> Node(>3>)> root.left.left>=> Node(>4>)> root.left.right>=> Node(>5>)> root.right.left>=> Node(>6>)> root.right.right>=> Node(>7>)> lca>=> findLCA(root,>4>,>5>)> if> lca>is> not> None>:> >print>(>'LCA(4, 5) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> lca>=> findLCA(root,>4>,>10>)> if> lca>is> not> None>:> >print>(>'LCA(4,10) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

using> System;> // c# implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >public> Node root;> >public> static> bool> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >public> virtual> Node findLCAUtil(Node node,>int> n1,> >int> n2)> >{> >// Base case> >if> (node ==>null>) {> >return> null>;> >}> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>) {> >return> temp;> >}> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>) {> >return> node;> >}> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >public> virtual> Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2) {> >return> lca;> >}> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Node lca = tree.findLCA(4, 5);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 5) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >lca = tree.findLCA(4, 10);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 10) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >}> }> // This code is contributed by Shrikant13>

Javascript

> // JavaScript implementation to find lowest> // common ancestor of n1 and n2 using one> // traversal of binary tree. It also handles> // cases even when n1 and n2 are not there in Tree> // Class containing left and right child> // of current node and key> class Node> {> >constructor(item)> >{> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> class BinaryTree{> > // Root of the Binary Tree> constructor()> {> >this>.root =>null>;> >this>.v1 =>false>;> >this>.v2 =>false>;> }> // This function returns pointer to LCA> // of two given values n1 and n2.> // v1 is set as true by this function> // if n1 is found> // v2 is set as true by this function> // if n2 is found> findLCAUtil(node, n1, n2)> {> > >// Base case> >if> (node ==>null>)> >{> >return> null>;> >}> > >// Store result in temp, in case of> >// key match so that we can search> >// for other key also.> >var> temp =>null>;> > >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as> >// true and return root (Note that if a key> >// is ancestor of other, then the ancestor> >// key becomes LCA)> >if> (node.data == n1)> >{> >this>.v1 =>true>;> >temp = node;> >}> >if> (node.data == n2)> >{> >this>.v2 =>true>;> >temp = node;> >}> > >// Look for keys in left and right subtrees> >var> left_lca =>this>.findLCAUtil(node.left, n1, n2);> >var> right_lca =>this>.findLCAUtil(node.right, n1, n2);> > >if> (temp !=>null>)> >{> >return> temp;> >}> > >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree and> >// other is present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >{> >return> node;> >}> > >// Otherwise check if left subtree or> >// right subtree is LCA> >return> left_lca !=>null> ? left_lca : right_lca;> }> // Finds lca of n1 and n2 under the> // subtree rooted with 'node'> findLCA(n1, n2)> {> > >// Initialize n1 and n2 as not visited> >this>.v1 =>false>;> >this>.v2 =>false>;> > >// Find lca of n1 and n2 using the> >// technique discussed above> >var> lca =>this>.findLCAUtil(>this>.root, n1, n2);> > >// Return LCA only if both n1 and n2> >// are present in tree> >if> (>this>.v1 &&>this>.v2)> >{> >return> lca;> >}> > >// Else return NULL> >return> null>;> }> }> // Driver code> var> tree =>new> BinaryTree();> tree.root =>new> Node(1);> tree.root.left =>new> Node(2);> tree.root.right =>new> Node(3);> tree.root.left.left =>new> Node(4);> tree.root.left.right =>new> Node(5);> tree.root.right.left =>new> Node(6);> tree.root.right.right =>new> Node(7);> var> lca = tree.findLCA(4, 5);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 5) = '> +> >lca.data +>' '>);> }>else> {> >document.write(>'Keys are not present'> +>' '>);> }> lca = tree.findLCA(4, 10);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 10) = '> +> >lca.data +>' '>);> }> else> {> >document.write(>'Keys are not present'> +>' '>);> }> // This code is contributed by rdtank> >

Izvade

LCA(4, 5) = 2 Keys are not present>

Laika sarežģītība : O(N), jo šī metode veic vienkāršu koka šķērsošanu augšupējā veidā.
Palīgtelpa: O(H), kur h ir koka augstums.

Izmantojot papildu datu struktūru (jaucēja tabulu):

The basic idea behind the 'Using an auxiliary data structure' approach for finding the lowest common ancestor of two nodes in a binary tree is to use a hash table or a map to store the parent pointers of each node. Once we have the parent pointers, we can traverse up from the first node and add all its ancestors to a set or a list. Then we can traverse up from the second node and check if each ancestor is already in the set or the list. The first ancestor that is already in the set or the list is the lowest common ancestor.>

Lai īstenotu iepriekš minēto pieeju, veiciet tālāk norādītās darbības.

Izveidojiet jaucējtabulu vai karti, lai saglabātu katra mezgla vecāku norādes binārajā kokā.
Brauciet pa bināro koku un aizpildiet jaucējtabulu vai karti ar katra mezgla vecākrādītājiem.
Sākot no pirmā mezgla, šķērsojiet koku un pievienojiet katru priekšteci kopai vai sarakstam.
Sākot no otrā mezgla, šķērsojiet koku un pārbaudiet, vai katrs sencis jau ir iekļauts kopā vai sarakstā. Pirmais priekštecis, kas jau ir komplektā vai sarakstā, ir zemākais kopējais sencis.
Ja kopīgs priekštecis netiek atrasts, atgrieziet nulli vai jebkuru citu vērtību, kas norāda, ka nav kopīga priekšteča.

Tālāk ir norādīta iepriekš minētās pieejas ieviešana.

C++

// C++ code to implement above approach> #include> #include> #include> #include> using> namespace> std;> // Definition of a binary tree node> struct> Node {> >int> data;> >Node* left;> >Node* right;> };> // Function to create a new binary tree node> Node* newNode(>int> data)> {> >Node* node =>new> Node;> >node->dati = dati;> >node->pa kreisi = NULL;> >node->pa labi = NULL;> >return> (node);> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> unordered_map buildParentMap(Node* root)> {> >unordered_map parentMap;> >parentMap[root] = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->pa kreisi) {> >parentMap[node->pa kreisi] = mezgls;> >queue.push_back(node->pa kreisi);> >}> >if> (node->pa labi) {> >parentMap[node->pa labi] = mezgls;> >queue.push_back(node->pa labi);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two nodes> // using an auxiliary data structure> int> findLCA(Node* root,>int> n1,>int> n2)> {> >// Build a hash table or a map of parent pointers for> >// each node in the tree> >unordered_map parentMap> >= buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node* p = NULL;> >Node* q = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->dati == n1) {> >p = node;> >}> >if> (node->dati == n2) {> >q = node;> >}> >if> (node->pa kreisi) {> >queue.push_back(node->pa kreisi);> >}> >if> (node->pa labi) {> >queue.push_back(node->pa labi);> >}> >}> >// Add all the ancestors of the first node to a set or a> >// list> >set ancestors;> >while> (p) {> >ancestors.insert(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if each> >// ancestor is already in the set or the list> >while> (q) {> >if> (ancestors.find(q) != ancestors.end()) {> >return> q> >->dati;>>>// already in the set or the list is> >// the lowest common ancestor> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> }> // Driver code> int> main()> {> >Node* root = newNode(1);> >root->pa kreisi = newNode(2);> >root->pa labi = newNode(3);> >root->pa kreisi->pa kreisi = newNode(4);> >root->pa kreisi->pa labi = newNode(5);> >root->pa labi-> pa kreisi = newNode(6);> >root->pa labi->pa labi = newNode(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5) << endl;> >cout <<>'LCA(4, 6) = '> << findLCA(root, 4, 6) << endl;> >cout <<>'LCA(3,4) = '> << findLCA(root, 3, 4) << endl;> >cout <<>'LCA(2, 4) = '> << findLCA(root, 2, 4) << endl;> >return> 0;> }> // This code is contributed by Veerendra_Singh_Rajpoot>

Java

import> java.util.*;> // Definition of a binary tree node> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> Main {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Map buildParentMap(Node root)> >{> >Map parentMap =>new> HashMap();> >parentMap.put(root,>null>);> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.left !=>null>) {> >parentMap.put(node.left, node);> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.put(node.right, node);> >queue.add(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> findLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Map parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.data == n1) {> >p = node;> >}> >if> (node.data == n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >queue.add(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >Set ancestors =>new> HashSet();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.contains(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> ->1>;>// No common ancestor found> >}> >public> static> void> main(String[] args)> >{> >Node root =>new> Node(>1>);> >root.left =>new> Node(>2>);> >root.right =>new> Node(>3>);> >root.left.left =>new> Node(>4>);> >root.left.right =>new> Node(>5>);> >root.right.left =>new> Node(>6>);> >root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ findLCA(root,>4>,>5>));> >System.out.println(>'LCA(4, 6) = '> >+ findLCA(root,>4>,>6>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>3>,>4>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>2>,>4>));> >}> }>

Python3

from> collections>import> deque> # Definition of a binary tree node> class> Node:> >def> __init__(>self>, data):> >self>.data>=> data> >self>.left>=> None> >self>.right>=> None> # Function to build a hash table or a map of parent> # pointers for each node in the tree> def> buildParentMap(root):> >parentMap>=> {}> >parentMap[root]>=> None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.left:> >parentMap[node.left]>=> node> >queue.append(node.left)> >if> node.right:> >parentMap[node.right]>=> node> >queue.append(node.right)> >return> parentMap> # Function to find the lowest common ancestor of two nodes> # using an auxiliary data structure> def> findLCA(root, n1, n2):> ># Build a hash table or a map of parent pointers for> ># each node in the tree> >parentMap>=> buildParentMap(root)> ># Find the nodes with values n1 and n2> >p, q>=> None>,>None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.data>=>=> n1:> >p>=> node> >if> node.data>=>=> n2:> >q>=> node> >if> node.left:> >queue.append(node.left)> >if> node.right:> >queue.append(node.right)> ># Add all the ancestors of the first node to a set or a> ># list> >ancestors>=> set>()> >while> p:> >ancestors.add(p)> >p>=> parentMap[p]> ># Traverse up from the second node and check if each> ># ancestor is already in the set or the list> >while> q:> >if> q>in> ancestors:> >return> q.data> >q>=> parentMap[q]> >return> ->1> # No common ancestor found> # Driver code> if> __name__>=>=> '__main__'>:> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>))> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>))> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>))> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>))>

C#

using> System;> using> System.Collections.Generic;> // Definition of a binary tree node> class> Node> {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> MainClass> {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Dictionary BuildParentMap(Node root)> >{> >Dictionary parentMap =>new> Dictionary();> >parentMap.Add(root,>null>);> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.left !=>null>)> >{> >parentMap.Add(node.left, node);> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >parentMap.Add(node.right, node);> >queue.Enqueue(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> FindLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Dictionary parentMap = BuildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.data == n1)> >{> >p = node;> >}> >if> (node.data == n2)> >{> >q = node;> >}> >if> (node.left !=>null>)> >{> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >queue.Enqueue(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >HashSet ancestors =>new> HashSet();> >while> (p !=>null>)> >{> >ancestors.Add(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>)> >{> >if> (ancestors.Contains(q))> >{> >return> q.data;> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> >}> >public> static> void> Main()> >{> >Node root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> + FindLCA(root, 4, 5));> >Console.WriteLine(>'LCA(4, 6) = '> + FindLCA(root, 4, 6));> >Console.WriteLine(>'LCA(3, 4) = '> + FindLCA(root, 3, 4));> >Console.WriteLine(>'LCA(2, 4) = '> + FindLCA(root, 2, 4));> >}> }> // This code is contributed by akashish__>

Javascript

// javascript code addition> // Definition of a binary tree node> class Node {> >constructor(item) {> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> function> buildParentMap(root) {> >const parentMap =>new> Map();> >parentMap.set(root,>null>);> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.left !=>null>) {> >parentMap.set(node.left, node);> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.set(node.right, node);> >queue.push(node.right);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two> // nodes using an auxiliary data structure> function> findLCA(root, n1, n2) {> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >const parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >let p =>null>, q =>null>;> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.data === n1) {> >p = node;> >}> >if> (node.data === n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >queue.push(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >const ancestors =>new> Set();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.has(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> -1;>// No common ancestor found> }> // Test the function> const root =>new> Node(1);> root.left =>new> Node(2);> root.right =>new> Node(3);> root.left.left =>new> Node(4);> root.left.right =>new> Node(5);> root.right.left =>new> Node(6);> root.right.right =>new> Node(7);> console.log(>'LCA(4, 5) = '> + findLCA(root, 4, 5));> console.log(>'LCA(4, 6) = '> + findLCA(root, 4, 6));> console.log(>'LCA(3, 4) = '> + findLCA(root, 3, 4));> console.log(>'LCA(2, 4) = '> + findLCA(root, 2, 4));> // The code is contributed by Nidhi goel.>

Izvade

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3,4) = 1 LCA(2, 4) = 2>

Laika sarežģītība: O(n),

Linux resursdators

Dotā koda laika sarežģītība ir O(n), kur n ir mezglu skaits binārajā kokā.

Lai izveidotu vecāku karti katram koka mezglam, katrs mezgls ir jāapmeklē vienu reizi, kas aizņem O(n) laiku. Lai atrastu mezglus ar vērtībām n1 un n2, katrs mezgls ir jāapmeklē vienu reizi, kas arī aizņem O(n) laiku. Braucot augšup no otrā mezgla un pārbaudot, vai katrs sencis jau ir kopā vai sarakstā, nepieciešams O(h) laiks, kur h ir binārā koka augstums.

Sliktākajā gadījumā binārā koka augstums ir O(n), ja binārais koks ir šķībs. Tāpēc dotā koda kopējā laika sarežģītība ir O(n) + O(n) + O(n) = O(n).

Telpas sarežģītība: O(n),

Dotā koda telpas sarežģītība sliktākajā gadījumā ir O(n). Tas ir tāpēc, ka katram koka mezglam izveidotās vecākkartes izmērs ir O(n). Turklāt priekšteču kopa var saturēt arī visus binārā koka mezglus sliktākajā gadījumā, kas arī aizņem O (n) vietu. Visbeidzot, rinda, ko izmanto binārā koka šķērsošanai, aizņem O (n) vietu. Tāpēc dotā koda kopējā telpas sarežģītība ir O(n) + O(n) + O(n) = O(n).

Mēs esam apsprieduši efektīvu risinājumu LCA atrašanai binārajā meklēšanas kokā. Binārajā meklēšanas kokā, izmantojot BST rekvizītus, mēs varam atrast LCA O(h) laikā, kur h ir koka augstums. Šāda ieviešana Binārajā kokā nav iespējama, jo atslēgas Binārā koka mezgli neievēro nekādu secību.

Iespējams, vēlēsities redzēt arī tālāk minētos rakstus:
LCA, izmantojot vecāku rādītāju
Zemākais kopīgais sencis binārajā meklēšanas kokā.
Atrodiet LCA binārajā kokā, izmantojot RMQ

TechCodeview

Zemākais kopīgais sencis binārajā kokā

Kas ir zemākais kopīgais priekštecis binārajā kokā?

Zemākā kopīgā priekšteča (LCA) pielietojums:

Zemākais kopīgais priekštecis binārajā kokā, saglabājot ceļus no saknes līdz n1 un saknes līdz n2:

C++

Java

Python3

C#

Javascript

Zemākais kopīgais priekštecis binārajā kokā, veicot vienu šķērsošanu:

C++

C

Java

Python3

C#

Javascript

C++

Java

Python3

C#

Javascript

C++

Java

Python3

C#

Javascript