Ņemot vērā divas virknes “X” un “Y”, atrodiet garākās kopīgās apakšvirknes garumu.
Piemēri:
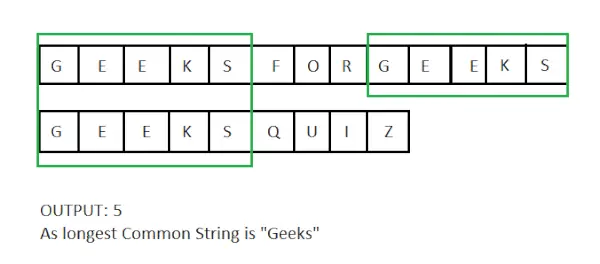
Ievade: X = techcodeview.com, y = GeeksQuiz
Izvade : 5
Paskaidrojums:
Garākā kopējā apakšvirkne ir Geeks, un tās garums ir 5.
Ievade: X = abcdxyz, y = xyzabcd
Izvade: 4
Paskaidrojums:
Garākā kopējā apakšvirkne ir abcd, un tās garums ir 4.Ievade: X = zxabcdezy, y = yzabcdezx
Izvade: 6
Paskaidrojums:
Garākā kopējā apakšvirkne ir abcdez, un tās garums ir 6.
Pieeja:
Apzīmēsim, ka m un n ir attiecīgi pirmās un otrās virknes garums.
A vienkāršs risinājums ir pa vienai izskatīt visas pirmās virknes apakšvirknes un katrai apakšvirknei pārbaudīt, vai tā ir otrās virknes apakšvirkne. Sekojiet līdzi maksimālā garuma apakšvirknei. Būs O(m^2) apakšvirknes, un mēs varam noskaidrot, vai virkne ir citas virknes apakšvirkne O(n) laikā (sk. šis ). Tātad šīs metodes kopējā laika sarežģītība būtu O (n * m2)
Dinamiskā programmēšana var izmantot, lai atrastu garāko kopējo apakšvirkni O(m*n) laikā. Ideja ir atrast garākā kopīgā sufiksa garumu visām abu virkņu apakšvirknēm un saglabāt šos garumus tabulā.
Garākajam kopējam sufiksam ir sekojoša optimāla apakšstruktūras īpašība.
Ja pēdējās rakstzīmes sakrīt, mēs samazinām abus garumus par 1
- LCSuff(X, Y, m, n) = LCSnepieciešams(X, Y, m-1, n-1) + 1, ja X[m-1] = Y[n-1]
Ja pēdējās rakstzīmes nesakrīt, rezultāts ir 0, t.i.,
- LCSuff(X, Y, m, n) = 0, ja (X[m-1] != Y[n-1])
Tagad mēs aplūkojam dažādu apakšvirkņu sufiksus, kas beidzas ar dažādiem indeksiem.
Maksimālais garums Garākā kopējā sufiksa ir garākā kopējā apakšvirkne.
LCSubStr(X, Y, m, n) = Max(LCSuff(X, Y, i, j)), kur 1 <= i <= m un 1 <= j <= n
Tālāk ir aprakstīta iepriekš minētā risinājuma iteratīva ieviešana.
C++
/* Dynamic Programming solution to> >find length of the> >longest common substring */> #include> #include> using> namespace> std;> /* Returns length of longest> >common substring of X[0..m-1]> >and Y[0..n-1] */> int> LCSubStr(>char>* X,>char>* Y,>int> m,>int> n)> {> >// Create a table to store> >// lengths of longest> >// common suffixes of substrings.> >// Note that LCSuff[i][j] contains> >// length of longest common suffix> >// of X[0..i-1] and Y[0..j-1].> >int> LCSuff[m + 1][n + 1];> >int> result = 0;>// To store length of the> >// longest common substring> >/* Following steps build LCSuff[m+1][n+1] in> >bottom up fashion. */> >for> (>int> i = 0; i <= m; i++)> >{> >for> (>int> j = 0; j <= n; j++)> >{> >// The first row and first column> >// entries have no logical meaning,> >// they are used only for simplicity> >// of program> >if> (i == 0 || j == 0)> >LCSuff[i][j] = 0;> >else> if> (X[i - 1] == Y[j - 1]) {> >LCSuff[i][j] = LCSuff[i - 1][j - 1] + 1;> >result = max(result, LCSuff[i][j]);> >}> >else> >LCSuff[i][j] = 0;> >}> >}> >return> result;> }> // Driver code> int> main()> {> >char> X[] =>'OldSite:techcodeview.com.org'>;> >char> Y[] =>'NewSite:GeeksQuiz.com'>;> >int> m =>strlen>(X);> >int> n =>strlen>(Y);> >cout <<>'Length of Longest Common Substring is '> ><< LCSubStr(X, Y, m, n);> >return> 0;> }> |
>
>
Java
// Java implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> import> java.io.*;> class> GFG {> >/*> >Returns length of longest common substring> >of X[0..m-1] and Y[0..n-1]> >*/> >static> int> LCSubStr(>char> X[],>char> Y[],>int> m,>int> n)> >{> >// Create a table to store> >// lengths of longest common> >// suffixes of substrings.> >// Note that LCSuff[i][j]> >// contains length of longest> >// common suffix of> >// X[0..i-1] and Y[0..j-1].> >// The first row and first> >// column entries have no> >// logical meaning, they are> >// used only for simplicity of program> >int> LCStuff[][] =>new> int>[m +>1>][n +>1>];> >// To store length of the longest> >// common substring> >int> result =>0>;> >// Following steps build> >// LCSuff[m+1][n+1] in bottom up fashion> >for> (>int> i =>0>; i <= m; i++) {> >for> (>int> j =>0>; j <= n; j++) {> >if> (i ==>0> || j ==>0>)> >LCStuff[i][j] =>0>;> >else> if> (X[i ->1>] == Y[j ->1>]) {> >LCStuff[i][j]> >= LCStuff[i ->1>][j ->1>] +>1>;> >result = Integer.max(result,> >LCStuff[i][j]);> >}> >else> >LCStuff[i][j] =>0>;> >}> >}> >return> result;> >}> >// Driver Code> >public> static> void> main(String[] args)> >{> >String X =>'OldSite:techcodeview.com.org'>;> >String Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.length();> >int> n = Y.length();> >System.out.println(> >'Length of Longest Common Substring is '> >+ LCSubStr(X.toCharArray(), Y.toCharArray(), m,> >n));> >}> }> // This code is contributed by Sumit Ghosh> |
>
>
Python3
# Python3 implementation of Finding> # Length of Longest Common Substring> # Returns length of longest common> # substring of X[0..m-1] and Y[0..n-1]> def> LCSubStr(X, Y, m, n):> ># Create a table to store lengths of> ># longest common suffixes of substrings.> ># Note that LCSuff[i][j] contains the> ># length of longest common suffix of> ># X[0...i-1] and Y[0...j-1]. The first> ># row and first column entries have no> ># logical meaning, they are used only> ># for simplicity of the program.> ># LCSuff is the table with zero> ># value initially in each cell> >LCSuff>=> [[>0> for> k>in> range>(n>+>1>)]>for> l>in> range>(m>+>1>)]> ># To store the length of> ># longest common substring> >result>=> 0> ># Following steps to build> ># LCSuff[m+1][n+1] in bottom up fashion> >for> i>in> range>(m>+> 1>):> >for> j>in> range>(n>+> 1>):> >if> (i>=>=> 0> or> j>=>=> 0>):> >LCSuff[i][j]>=> 0> >elif> (X[i>->1>]>=>=> Y[j>->1>]):> >LCSuff[i][j]>=> LCSuff[i>->1>][j>->1>]>+> 1> >result>=> max>(result, LCSuff[i][j])> >else>:> >LCSuff[i][j]>=> 0> >return> result> # Driver Code> X>=> 'OldSite:techcodeview.com.org'> Y>=> 'NewSite:GeeksQuiz.com'> m>=> len>(X)> n>=> len>(Y)> print>(>'Length of Longest Common Substring is'>,> >LCSubStr(X, Y, m, n))> # This code is contributed by Soumen Ghosh> |
>
>
C#
// C# implementation of finding length of longest> // Common substring using Dynamic Programming> using> System;> class> GFG {> >// Returns length of longest common> >// substring of X[0..m-1] and Y[0..n-1]> >static> int> LCSubStr(>string> X,>string> Y,>int> m,>int> n)> >{> >// Create a table to store lengths of> >// longest common suffixes of substrings.> >// Note that LCSuff[i][j] contains length> >// of longest common suffix of X[0..i-1]> >// and Y[0..j-1]. The first row and first> >// column entries have no logical meaning,> >// they are used only for simplicity of> >// program> >int>[, ] LCStuff =>new> int>[m + 1, n + 1];> >// To store length of the longest common> >// substring> >int> result = 0;> >// Following steps build LCSuff[m+1][n+1]> >// in bottom up fashion> >for> (>int> i = 0; i <= m; i++)> >{> >for> (>int> j = 0; j <= n; j++)> >{> >if> (i == 0 || j == 0)> >LCStuff[i, j] = 0;> >else> if> (X[i - 1] == Y[j - 1])> >{> >LCStuff[i, j]> >= LCStuff[i - 1, j - 1] + 1;> >result> >= Math.Max(result, LCStuff[i, j]);> >}> >else> >LCStuff[i, j] = 0;> >}> >}> >return> result;> >}> >// Driver Code> >public> static> void> Main()> >{> >String X =>'OldSite:techcodeview.com.org'>;> >String Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.Length;> >int> n = Y.Length;> >Console.Write(>'Length of Longest Common'> >+>' Substring is '> >+ LCSubStr(X, Y, m, n));> >}> }> // This code is contributed by Sam007.> |
>
>
Javascript
> // JavaScript implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> >/*> >Returns length of longest common> >substring of X[0..m-1] and Y[0..n-1]> >*/> >function> LCSubStr( X, Y , m , n) {> >// Create a table to store> >// lengths of longest common> >// suffixes of substrings.> >// Note that LCSuff[i][j]> >// contains length of longest> >// common suffix of> >// X[0..i-1] and Y[0..j-1].> >// The first row and first> >// column entries have no> >// logical meaning, they are> >// used only for simplicity of program> > >var> LCStuff => >Array(m + 1).fill().map(()=>Masīvs(n + 1).fill(0));> >// To store length of the longest> >// common substring> >var> result = 0;> >// Following steps build> >// LCSuff[m+1][n+1] in bottom up fashion> >for> (i = 0; i <= m; i++) {> >for> (j = 0; j <= n; j++) {> >if> (i == 0 || j == 0)> >LCStuff[i][j] = 0;> >else> if> (X[i - 1] == Y[j - 1]) {> >LCStuff[i][j] = LCStuff[i - 1][j - 1] + 1;> >result = Math.max(result, LCStuff[i][j]);> >}>else> >LCStuff[i][j] = 0;> >}> >}> >return> result;> >}> >// Driver Code> > >var> X =>'OldSite:techcodeview.com.org'>;> >var> Y =>'NewSite:GeeksQuiz.com'>;> >var> m = X.length;> >var> n = Y.length;> >document.write(>'Length of Longest Common Substring is '> +> >LCSubStr(X, Y, m, n));> // This code contributed by Rajput-Ji> > |
>
>
PHP
// Dynamic Programming solution to find // length of the longest common substring // Returns length of longest common // substring of X[0..m-1] and Y[0..n-1] function LCSubStr($X, $Y, $m, $n) { // Create a table to store lengths of // longest common suffixes of substrings. // Notethat LCSuff[i][j] contains length // of longest common suffix of X[0..i-1] // and Y[0..j-1]. The first row and // first column entries have no logical // meaning, they are used only for // simplicity of program $LCSuff = array_fill(0, $m + 1, array_fill(0, $n + 1, NULL)); $result = 0; // To store length of the // longest common substring // Following steps build LCSuff[m+1][n+1] // in bottom up fashion. for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++) { if ($i == 0 || $j == 0) $LCSuff[$i][$j] = 0; else if ($X[$i - 1] == $Y[$j - 1]) { $LCSuff[$i][$j] = $LCSuff[$i - 1][$j - 1] + 1; $result = max($result, $LCSuff[$i][$j]); } else $LCSuff[$i][$j] = 0; } } return $result; } // Driver Code $X = 'OldSite:techcodeview.com.org'; $Y = 'NewSite:GeeksQuiz.com'; $m = strlen($X); $n = strlen($Y); echo 'Length of Longest Common Substring is ' . LCSubStr($X, $Y, $m, $n); // This code is contributed by ita_c ?>>> |
>Length of Longest Common Substring is 10>
Laika sarežģītība: O(m*n)
Palīgtelpa: O(m*n), jo ir aizņemta m*n papildu vieta.
Cita pieeja: (Kosmosa optimizēta pieeja).
Iepriekš minētajā pieejā mēs izmantojam tikai pēdējo 2-D masīva rindu, tāpēc mēs varam optimizēt telpu, izmantojot
2-D masīvs ar izmēru 2*(min(n,m)).
Tālāk ir aprakstīta iepriekš minētās pieejas īstenošana.
C++
#include> #include> using> namespace> std;> // Function to find the length of the longest LCS> int> LCSubStr(string s, string t,>int> n,>int> m)> {> >// Create DP table> >vectorint>> dp(n + 1, vektors |
>
>
Java
xd nozīme
// Java implementation of the above approach> import> java.io.*;> class> GFG> {> > >// Function to find the length of the> >// longest LCS> >static> int> LCSubStr(String s,String t,> >int> n,>int> m)> >{> > >// Create DP table> >int> dp[][]=>new> int>[>2>][m+>1>];> >int> res=>0>;> > >for>(>int> i=>1>;i<=n;i++)> >{> >for>(>int> j=>1>;j<=m;j++)> >{> >if>(s.charAt(i->1>)==t.charAt(j->1>))> >{> >dp[i%>2>][j]=dp[(i->1>)%>2>][j->1>]+>1>;> >if>(dp[i%>2>][j]>res)> >res=dp[i%>2>][j];> >}> >else> dp[i%>2>][j]=>0>;> >}> >}> >return> res;> >}> > >// Driver Code> >public> static> void> main (String[] args)> >{> >String X=>'OldSite:techcodeview.com.org'>;> >String Y=>'NewSite:GeeksQuiz.com'>;> > >int> m=X.length();> >int> n=Y.length();> > >// Function call> >System.out.println(LCSubStr(X,Y,m,n));> > >}> }> |
>
>
Python3
# Python implementation of the above approach> # Function to find the length of the> # longest LCS> def> LCSubStr(s, t, n, m):> > ># Create DP table> >dp>=> [[>0> for> i>in> range>(m>+> 1>)]>for> j>in> range>(>2>)]> >res>=> 0> > >for> i>in> range>(>1>,n>+> 1>):> >for> j>in> range>(>1>,m>+> 1>):> >if>(s[i>-> 1>]>=>=> t[j>-> 1>]):> >dp[i>%> 2>][j]>=> dp[(i>-> 1>)>%> 2>][j>-> 1>]>+> 1> >if>(dp[i>%> 2>][j]>res):> >res>=> dp[i>%> 2>][j]> >else>:> >dp[i>%> 2>][j]>=> 0> >return> res> # Driver Code> X>=> 'OldSite:techcodeview.com.org'> Y>=> 'NewSite:GeeksQuiz.com'> m>=> len>(X)> n>=> len>(Y)> # Function call> print>(LCSubStr(X,Y,m,n))> # This code is contributed by avanitrachhadiya2155> |
>
>
C#
// C# implementation of the above approach> using> System;> public> class> GFG> {> >// Function to find the length of the> >// longest LCS> >static> int> LCSubStr(>string> s,>string> t,> >int> n,>int> m)> >{> >// Create DP table> >int>[,] dp =>new> int>[2, m + 1];> >int> res = 0;> >for>(>int> i = 1; i <= n; i++)> >{> >for>(>int> j = 1; j <= m; j++)> >{> >if>(s[i - 1] == t[j - 1])> >{> >dp[i % 2, j] = dp[(i - 1) % 2, j - 1] + 1;> >if>(dp[i % 2, j]>res)> >res = dp[i % 2, j];> >}> >else> dp[i % 2, j] = 0;> >}> >}> >return> res;> >}> >// Driver Code> >static> public> void> Main (){> >string> X =>'OldSite:techcodeview.com.org'>;> >string> Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.Length;> >int> n = Y.Length;> >// Function call> >Console.WriteLine(LCSubStr(X,Y,m,n));> >}> }> // This code is contributed by rag2127> |
>
>
Javascript
> // JavaScript implementation of the above approach> >// Function to find the length of the> >// longest LCS> >function> LCSubStr(s, t, n, m)> >{> > >// Create DP table> >var> dp = Array(2).fill().map(()=>Masīvs(m+1).fill(0));> >var> res = 0;> > >for>(>var> i = 1; i <= n; i++)> >{> >for>(>var> j = 1; j <= m; j++)> >{> >if>(s.charAt(i - 1) == t.charAt(j - 1))> >{> >dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1;> >if>(dp[i % 2][j]>res)> >res = dp[i % 2][j];> >}> >else> dp[i % 2][j] = 0;> >}> >}> >return> res;> >}> > >// Driver Code> >var> X =>'OldSite:techcodeview.com.org'>;> >var> Y =>'NewSite:GeeksQuiz.com'>;> > >var> m = X.length;> >var> n = Y.length;> > >// Function call> >document.write(LCSubStr(X, Y, m, n));> // This code is contributed by shivanisinghss2110> > |
>
>Izvade
10>
Laika sarežģītība: O(n*m)
Palīgtelpa: O(min(m,n))
Cita pieeja: (Izmantojot rekursiju)
Šeit ir iepriekš minētās pieejas rekursīvais risinājums.
C++
// C++ program using to find length of the> // longest common substring recursion> #include> using> namespace> std;> string X, Y;> // Returns length of function f> // or longest common substring> // of X[0..m-1] and Y[0..n-1]> int> lcs(>int> i,>int> j,>int> count)> {> >if> (i == 0 || j == 0)> >return> count;> >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = max(count,> >max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> }> // Driver code> int> main()> {> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.size();> >m = Y.size();> >cout << lcs(n, m, 0);> >return> 0;> }> |
>
>
Java
// Java program using to find length of the> // longest common substring recursion> import> java.io.*;> class> GFG {> >static> String X, Y;> >// Returns length of function> >// for longest common> >// substring of X[0..m-1] and Y[0..n-1]> >static> int> lcs(>int> i,>int> j,>int> count)> >{> >if> (i ==>0> || j ==>0>)> >{> >return> count;> >}> >if> (X.charAt(i ->1>)> >== Y.charAt(j ->1>))> >{> >count = lcs(i ->1>, j ->1>, count +>1>);> >}> >count = Math.max(count,> >Math.max(lcs(i, j ->1>,>0>),> >lcs(i ->1>, j,>0>)));> >return> count;> >}> > >// Driver code> >public> static> void> main(String[] args)> >{> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.length();> >m = Y.length();> >System.out.println(lcs(n, m,>0>));> >}> }> // This code is contributed by Rajput-JI> |
>
>
Python3
# Python3 program using to find length of> # the longest common substring recursion> # Returns length of function for longest> # common substring of X[0..m-1] and Y[0..n-1]> def> lcs(i, j, count):> >if> (i>=>=> 0> or> j>=>=> 0>):> >return> count> >if> (X[i>-> 1>]>=>=> Y[j>-> 1>]):> >count>=> lcs(i>-> 1>, j>-> 1>, count>+> 1>)> >count>=> max>(count,>max>(lcs(i, j>-> 1>,>0>),> >lcs(i>-> 1>, j,>0>)))> >return> count> # Driver code> if> __name__>=>=> '__main__'>:> >X>=> 'abcdxyz'> >Y>=> 'xyzabcd'> >n>=> len>(X)> >m>=> len>(Y)> >print>(lcs(n, m,>0>))> # This code is contributed by Ryuga> |
>
>
C#
// C# program using to find length> // of the longest common substring> // recursion> using> System;> class> GFG {> >static> String X, Y;> >// Returns length of function for> >// longest common substring of> >// X[0..m-1] and Y[0..n-1]> >static> int> lcs(>int> i,>int> j,>int> count)> >{> >if> (i == 0 || j == 0) {> >return> count;> >}> >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = Math.Max(count, Math.Max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> >}> >// Driver code> >public> static> void> Main()> >{> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.Length;> >m = Y.Length;> >Console.Write(lcs(n, m, 0));> >}> }> // This code is contributed by Rajput-JI> |
>
>
Javascript
> >// Javascript program using to find length of the> >// longest common substring recursion> >let X, Y;> > >// Returns length of function f> >// or longest common substring> >// of X[0..m-1] and Y[0..n-1]> >function> lcs(i, j, count)> >{> > >if> (i == 0 || j == 0)> >return> count;> > >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = Math.max(count,> >Math.max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> >}> > >let n, m;> > >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> > >n = X.length;> >m = Y.length;> > >document.write(lcs(n, m, 0));> > >// This code is contributed by divyeshrabadiya07.> > |
>
>
PHP
// PHP program using to find length of the // longest common substring recursion // Returns length of function for // longest common substring of // X[0..m-1] and Y[0..n-1] function lcs($i, $j, $count, &$X, &$Y) { if ($i == 0 || $j == 0) return $count; if ($X[$i - 1] == $Y[$j - 1]) { $count = lcs($i - 1, $j - 1, $count + 1, $X, $Y); } $count = max($count, lcs($i, $j - 1, 0, $X, $Y), lcs($i - 1, $j, 0, $X, $Y)); return $count; } // Driver code $X = 'abcdxyz'; $Y = 'xyzabcd'; $n = strlen($X); $m = strlen($Y); echo lcs($n, $m, 0, $X, $Y); // This code is contributed // by rathbhupendra ?>>> |
>4>
Laika sarežģītība : O(2^maks.(m,n)) jo funkcija veic divus rekursīvus izsaukumus – lcs(i, j-1, 0) un lcs(i-1, j, 0), kad rakstzīmes pie X[i-1] != Y[j-1]. Tātad tas nodrošinās sliktākā gadījuma laika sarežģītību kā 2^N, kur N = max(m, n), m un n ir X un Y virknes garums.
Palīgtelpa: O(1): jo funkcijas izsaukums neizmanto papildu vietu (funkcija izmanto tikai rekursīvu izsaukumu steku, ko mēs parasti neņemam vērā palīgtelpā).
