Lineārā programmēšana ir matemātisks jēdziens, ko izmanto, lai atrastu optimālo lineārās funkcijas risinājumu. Šī metode izmanto vienkāršus pieņēmumus dotās funkcijas optimizēšanai. Lineārajai programmēšanai ir milzīga reālās pasaules lietojumprogramma, un to izmanto dažādu veidu problēmu risināšanai.
Lineārā programmēšana tiek izmantota dažādās nozarēs, piemēram, kuģniecības nozarēs, ražošanas nozarēs, transporta nozarēs, telekomunikācijās un citās.
Termins 'lineārā programmēšana' sastāv no diviem vārdiem 'lineārais' un 'programmēšana', vārds 'lineārais' norāda uz saikni starp dažāda veida mainīgajiem, kuru viena pakāpe tiek izmantota uzdevumā, un vārds 'programmēšana' norāda uz soli pa solim šo problēmu risināšanas procedūru.
Šajā rakstā mēs detalizēti uzzināsim par lineāro programmēšanu, tās piemēriem, formulām un citiem jēdzieniem.
Satura rādītājs
- Kas ir lineārā programmēšana?
- Lineārās programmēšanas sastāvdaļas
- Lineārās programmēšanas piemēri
- Lineārās programmēšanas problēmas
- Lineārās programmēšanas problēmu veidi
- Lineārās programmēšanas formula
- Kā atrisināt lineārās programmēšanas problēmas?
- Lineārās programmēšanas metodes
- Lineārās programmēšanas vienkāršās metodes
- Lineārās programmēšanas grafiskā metode
- Lineārās programmēšanas lietojumprogrammas
- Lineārās programmēšanas nozīme
- Jaunākie lineārās programmēšanas pielietojumi
- Lineārā programmēšana operāciju izpētē
- Simpleksā metode
Kas ir lineārā programmēšana?
Lineārā programmēšana vai Lineārā optimizācija ir paņēmiens, kas palīdz mums atrast optimālo risinājumu konkrētai problēmai, optimālais risinājums ir risinājums, kas ir labākais iespējamais konkrētas problēmas iznākums.
Vienkārši izsakoties, tā ir metode, kā uzzināt, kā kaut ko izdarīt vislabākajā iespējamajā veidā. Ar ierobežotiem resursiem jums ir nepieciešams optimāli izmantot resursus un sasniegt vislabāko iespējamo rezultātu konkrētam mērķim, piemēram, ar viszemākajām izmaksām, augstāko rezervi vai mazāko laiku.
Situācija, kurā ir jāmeklē labākās mainīgo vērtības, kas pakļautas noteiktiem ierobežojumiem, ir tāda, kurā mēs izmantojam lineārās programmēšanas problēmas. Šīs situācijas nevar atrisināt ar parastajiem aprēķinu un skaitļu paņēmieniem.
Lineārās programmēšanas definīcija
Lineārā programmēšana ir metode, ko izmanto konkrēta scenārija optimizēšanai. Lineārās programmēšanas izmantošana sniedz mums vislabāko iespējamo rezultātu noteiktā situācijā. Tas izmanto visus pieejamos resursus tā, lai tie radītu optimālu rezultātu.
Lineārās programmēšanas sastāvdaļas
Lineārās programmēšanas (LP) problēmas pamatkomponenti ir:
- Lēmuma mainīgie: Mainīgie lielumi, kurus vēlaties noteikt, lai sasniegtu optimālo risinājumu.
- Mērķa funkcija: M atemātisks vienādojums, kas atspoguļo mērķi, kuru vēlaties sasniegt
- Ierobežojumi: Ierobežojumi vai ierobežojumi, kas jāievēro jūsu lēmumu mainīgajiem.
- Ierobežojumi, kas nav negatīvi: Dažos reālās pasaules scenārijos, lēmumu mainīgie nevar būt negatīvi
Lineārās programmēšanas papildu īpašības
- Galīgums: Lēmuma mainīgo un ierobežojumu skaits LP uzdevumā ir ierobežots.
- Linearitāte: Mērķa funkcijai un visiem ierobežojumiem ir jābūt lēmuma mainīgo lineārām funkcijām . Tas nozīmē, ka mainīgo lielumu pakāpei jābūt vienai.
Lineārās programmēšanas piemēri
Mēs varam saprast situācijas, kurās tiek izmantota lineārā programmēšana, izmantojot tālāk apskatīto piemēru,
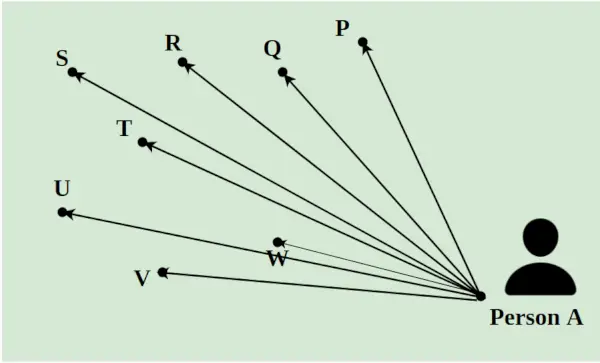
Pieņemsim, ka piegādātājam ir jāpiegādā 8 paciņas dienā uz dažādām pilsētas vietām. Viņam ir jāizvēlas visas paketes no A un jānogādā tās uz punktiem P, Q, R, S, T, U, V un W. Attālums starp tām ir norādīts, izmantojot līnijas, kā parādīts attēlā zemāk. Īsākais ceļš, ko iet piegādātājs, tiek aprēķināts, izmantojot lineārās programmēšanas koncepciju.
lejupielādējiet youtube videoklipus vlc
Lineārās programmēšanas problēmas
Lineārās programmēšanas problēmas (LPP) ietver lineāras funkcijas optimizāciju, lai atrastu funkcijas optimālo vērtību risinājumu. Optimālā vērtība var būt gan maksimālā, gan minimālā vērtība.
LPP tiek izsauktas lineārās funkcijas objektīvās funkcijas. Mērķa funkcijai var būt vairāki mainīgie, kas ir pakļauti nosacījumiem un kuriem ir jāatbilst lineāri ierobežojumi .
Lineārās programmēšanas problēmu veidi
Ir daudz dažādu lineārās programmēšanas problēmu (LPP), taču šajā rakstā mēs aplūkosim trīs galvenās lineārās programmēšanas problēmas.
Ražošanas problēmas
Ražošanas problēmas ir problēma, kas attiecas uz to vienību skaitu, kas būtu jāsaražo vai jāpārdod, lai palielinātu peļņu, ja katram produktam ir nepieciešams fiksēts darbaspēks, mašīnas stundas un izejvielas.
Diētas problēmas
To izmanto, lai aprēķinātu dažādu veidu uzturā iekļaujamo sastāvdaļu skaitu, lai iegūtu minimālās izmaksas atkarībā no pārtikas pieejamības un to cenām.
Transporta problēmas
To izmanto, lai noteiktu transportēšanas grafiku, lai atrastu lētāko veidu, kā transportēt produktu no ražotnēm/rūpnīcām, kas atrodas dažādās vietās, uz dažādiem tirgiem.
Lineārās programmēšanas formula
Lineārās programmēšanas problēma sastāv no:
- Lēmumu mainīgie
- Objektīvā funkcija
- Ierobežojumi
- Nenegatīvi ierobežojumi
Lēmumu mainīgie ir mainīgie x un y, kas nosaka lineārās programmēšanas problēmas izvadi un attēlo galīgo risinājumu.
The mērķa funkcija , ko parasti apzīmē ar Z, ir lineāra funkcija, kas ir jāoptimizē atbilstoši dotajam nosacījumam, lai iegūtu galīgo risinājumu.
The ierobežojumiem Uzliek lēmumu mainīgajiem, kas ierobežo to vērtības, sauc par ierobežojumiem.
Tagad lineārās programmēšanas problēmas vispārējā formula ir:
Mērķa funkcija : Z = cirvis + by
Ierobežojumi: cx + dy ≥ e, px + qy ≤ r
Nenegatīvi ierobežojumi: x ≥ 0, y ≥ 0
Iepriekš minētajā nosacījumā x un y ir lēmuma mainīgie.
Kā atrisināt lineārās programmēšanas problēmas?
Pirms lineārās programmēšanas uzdevumu risināšanas vispirms ir jāformulē uzdevumi atbilstoši standarta parametriem. Lineārās programmēšanas problēmu risināšanas soļi ir šādi:
1. darbība: Atzīmējiet uzdevumā lēmumu mainīgos.
2. darbība: Izveidojiet problēmas mērķa funkciju un pārbaudiet, vai funkcija ir jāsamazina vai jāpalielina.
3. darbība: Pierakstiet visus lineāro uzdevumu ierobežojumus.
4. darbība: Nodrošiniet lēmumu mainīgo lielumu nenegatīvus ierobežojumus.
5. darbība: Tagad atrisiniet lineārās programmēšanas problēmu, izmantojot jebkuru metodi, parasti mēs izmantojam vai nu simplekso, vai grafisko metodi.
Lineārās programmēšanas metodes
Lineārās programmēšanas uzdevumu risināšanai izmantojam dažādas metodes. Divas visbiežāk izmantotās metodes ir:
- Simpleksā metode
- Grafiskā metode
Šajā rakstā sīkāk uzzināsim par šīm divām metodēm,
Lineārās programmēšanas vienkāršās metodes
Viena no visizplatītākajām metodēm lineārās programmēšanas problēmas risināšanai ir vienkāršā metode. Šajā metodē mēs atkārtojam noteiktu nosacījumu “n” vairākas reizes, līdz tiek sasniegts optimālais risinājums.
Lai atrisinātu lineārās programmēšanas problēmas, izmantojot simplekso metodi, jāveic šādas darbības:
1. darbība: Formulējiet lineārās programmēšanas problēmas, pamatojoties uz dotajiem ierobežojumiem.
2. darbība: Pārvērtiet visas dotās nevienādības lineārās programmēšanas problēmu vienādojumos vai vienādībās, pievienojot katrai nevienādībai atslābuma mainīgo, kur tas ir nepieciešams.
3. darbība: Izveidojiet sākotnējo simpleksa tabulu. Attēlojot katru ierobežojuma vienādojumu pēc kārtas un ierakstot mērķa funkciju apakšējā rindā. Šādi iegūto tabulu sauc par Simplex tabulu.
4. darbība: Identificējiet lielāko negatīvo ierakstu apakšējā rindā, elementa kolonnu ar augstāko negatīvo ierakstu sauc par pivot kolonnu
5. darbība: Sadaliet galējās labās kolonnas ierakstus ar attiecīgās šarnīra kolonnas ierakstiem, izslēdzot apakšējās rindas ierakstus. Tagad rinda, kurā ir vismazākais ieraksts, tiek saukta par pagrieziena rindu. Pagrieziena elements tiek iegūts, krustojoties pagrieziena rindai un pagrieziena kolonnai.
6. darbība: Izmantojot matricas operāciju un ar pivot elementa palīdzību, visus ierakstus pivot kolonnā padariet par nullēm.
7. darbība: Pārbaudiet, vai apakšējā rindā nav negatīvu ierakstu, ja apakšējā rindā nav negatīvu ierakstu, pabeidziet procesu, pretējā gadījumā sāciet procesu vēlreiz no 4. darbības.
8. darbība: Tā iegūtā galīgā vienkāršā tabula sniedz mūsu problēmas risinājumu.
Lineārās programmēšanas grafiskā metode
Grafiskā metode ir cita metode, nevis Simplex metode, ko izmanto lineārās programmēšanas problēmu risināšanai. Kā norāda nosaukums, šī metode izmanto grafikus, lai atrisinātu dotās lineārās programmēšanas problēmas. Šī ir labākā metode lineārās programmēšanas problēmu risināšanai un prasa mazāk pūļu nekā vienkāršā metode.
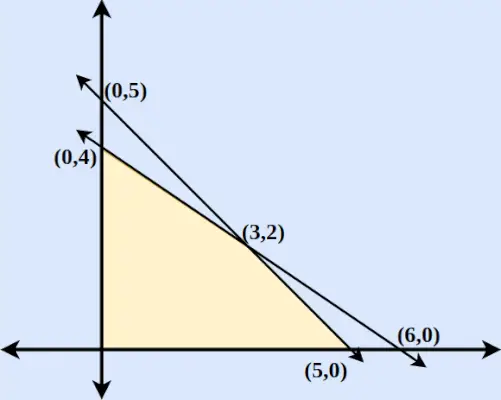
Izmantojot šo metodi, mēs attēlojam visas nevienādības, kas ir pakļautas ierobežojumiem dotajās lineārās programmēšanas problēmās. Tiklīdz visas dotās LPP nevienādības ir attēlotas XY grafikā, visu nevienādību kopējais apgabals dod optimālo risinājumu. Tiek aprēķināti visi iespējamā reģiona stūra punkti un visos šajos punktos tiek aprēķināta mērķa funkcijas vērtība, tad, salīdzinot šīs vērtības, iegūstam optimālo LPP risinājumu.
Piemērs: atrodiet z = 6x + 9y maksimālo un minimālo vērtību, ja ierobežojuma nosacījumi ir,
- 2x + 3y ≤ 12
- x un y ≥ 0
- x + y ≤ 5
Risinājums:
1. darbība : vispirms pārveidojiet vienādojumus parastajos vienādojumos. Tādējādi vienādojumi būs 2x+3y = 0, x = 0, y = 0 un x + y = 5.
2. darbība : atrodiet punktus, kuros 2x + 3y un x + y = 5 sagriež x asi un y asi. Lai atrastu x ass krustošanās punktu, attiecīgajā vienādojumā ievietojiet y = 0 un atrodiet punktu. Līdzīgi y ass krustošanās punktiem ielieciet x = 0 attiecīgajā vienādojumā.
3. darbība : uzzīmējiet divas līnijas, kas sagriež x asi un y asi. Mēs atklājam, ka abas asis sagriež viena otru pie (3, 2).
4. darbība : Ja x ≥ 0 un y ≥ 0, mēs atklājam, ka tiek ievēroti abi vienādojumi. Tādējādi reģions ietvers apgabala reģionu, ko norobežo divas asis un abas līnijas, ieskaitot izcelsmi. Uzzīmētais reģions ir parādīts zemāk attēlā.
5. darbība : Atrodiet Z katram punktam un maksimumus un minimumus.
Koordinātas Z = 6x + 9 g (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3.2) Z = 36 Tādējādi mēs atklājam, ka Z = 6x + 9y ir maksimālais pie (0,5) un minimālais pie (5,0).
Lineārās programmēšanas lietojumprogrammas
Lineārajai programmēšanai ir lietojumprogrammas dažādās jomās. To izmanto, lai noteiktu procesa minimālās izmaksas, ja ir norādīti visi problēmu ierobežojumi. To izmanto, lai optimizētu transportlīdzekļa transportēšanas izmaksas utt. Lineārās programmēšanas lietojumprogrammas ir dažādas
Inženierrūpniecības
Engineering Industries izmanto lineāro programmēšanu, lai atrisinātu projektēšanas un ražošanas problēmas un iegūtu maksimālu produkciju no noteiktā stāvokļa.
Ražošanas nozares
Ražošanas nozares izmanto lineāro programmēšanu, lai palielinātu uzņēmumu peļņu un samazinātu ražošanas izmaksas.
Enerģētikas nozares
Enerģētikas uzņēmumi izmanto lineāro programmēšanu, lai optimizētu savu ražošanas jaudu.
Transporta nozares
Lineārā programmēšana tiek izmantota arī transporta nozarēs, lai atrastu ceļu, kā samazināt transporta izmaksas.
Lineārās programmēšanas nozīme
Lineārajai programmēšanai ir milzīga nozīme dažādās nozarēs, tā palielina izvades vērtību, vienlaikus samazinot ievades vērtības atbilstoši dažādiem ierobežojumiem.
LP ir ļoti piemērojams, ja problēmas risināšanas laikā mums ir vairāki nosacījumi un mums ir jāoptimizē problēmas izvade, t.i., mums ir jāatrod minimālā vai maksimālā vērtība atbilstoši konkrētajam nosacījumam.
Lasīt vairāk,
- Lineārās nevienādības
- Lineāro nevienādību algebriskais risinājums
Lineārās programmēšanas problēmas
1. problēma: Uzņēmums ražo un pārdod divu veidu produktus, un katras vienības a un b ražošanas izmaksas ir attiecīgi 200 un 150 rūpijas, katra produkta vienība dod peļņu 20 rūpiju apmērā un katra produkta b vienība dod peļņu 15 rūpijas, pārdodot. . Uzņēmums lēš, ka A un B ikmēneša pieprasījums ir maksimāli no novāktās vienības visā mēneša ražošanas budžetā ir noteikts 50 000 rūpiju. Cik vienību uzņēmumam vajadzētu ražot, lai gūtu maksimālu peļņu no ikmēneša pārdošanas no un b?
Risinājums:
Pieņemsim, ka x = A tipa vienību skaits
y = B tipa vienību skaits
Maksimizēt Z = 40x + 50 g
Ievērojot ierobežojumus
3x + y ≤ 9
x + 2y ≤ 8
un x, y ≥ 0
Apsveriet vienādojumu,
3x + y = 9
x = 3
y = 0
un x + 2y = 8
x = 8
y = 0
Tagad mēs varam noteikt Z maksimālo vērtību, novērtējot Z vērtību četros punktos (virsotnēs), kas parādīts zemāk
Virsotnes
Z = 40x + 50 g
(0, 0)
Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
Maksimālā peļņa, Z = Rs. 230
∴ A tipa vienību skaits ir 2 un B tipa vienību skaits ir 3.
atkārtojiet, izmantojot karti java
2. problēma: maksimizēt Z = 3x + 4y.
Ievērojot ierobežojumus , x + y ≤ 450, 2x + y ≤ 600 un x, y ≤ 0.
Risinājums:
Mums ir no dotā
Ierobežojumi (1)
X + Y = 450
Liekot x = 0, ⇒ 0 + y = 450 ⇒ y = 450
y = 0, ⇒ x + 0 = 450 ⇒ x = 450
No, Ierobežojumi (2)
2x + y = 600
Liekot x = 0, ⇒ 0 + y = 600 ⇒ y = 600
y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Tagad mums ir punktu koordināte Z = 3x + 4y
| Virsotnes | Z = 3x + 4 g |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300+ 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Tāpēc optimālais risinājuma maksimums Z = 1800 pie koordinātām x = 0 un y = 450. Grafiks ir dots zemāk.

Jaunākie lineārās programmēšanas pielietojumi
Lineārā programmēšana, jaudīga matemātiska tehnika, tiek izmantota optimizācijas problēmu risināšanai dažādās nozarēs. Šeit ir dažas modernas lietojumprogrammas:
- Piegādes ķēdes optimizācija : Lineārā programmēšana palīdz uzņēmumiem samazināt izmaksas un palielināt piegādes ķēžu efektivitāti. To izmanto, lai noteiktu visrentablākos transportēšanas maršrutus, noliktavas operācijas un krājumu pārvaldības stratēģijas.
- Enerģijas pārvaldība : Enerģētikas nozarē lineāro programmēšanu izmanto, lai optimizētu enerģijas ražošanas metožu kombināciju. Tas ietver tradicionālo enerģijas avotu līdzsvarošanu ar atjaunojamiem, lai samazinātu izmaksas un ietekmi uz vidi, vienlaikus apmierinot pieprasījumu.
- Telekomunikāciju tīklu projektēšana : Lineārā programmēšana palīdz efektīvu telekomunikāciju tīklu projektēšanā. Tas palīdz piešķirt joslas platumu, izstrādāt tīkla izkārtojumus un optimizēt datu plūsmu, lai nodrošinātu ātrdarbīgu komunikāciju par zemākām izmaksām.
- Finanšu plānošana : Uzņēmumi un finanšu analītiķi izmanto lineāro programmēšanu portfeļa optimizācijai, riska pārvaldībai un kapitāla budžeta veidošanai. Tas palīdz pieņemt lēmumus par ieguldījumiem, kas palielina peļņu, vienlaikus samazinot risku.
- Veselības aprūpes loģistika : veselības aprūpē tiek izmantota lineārā programmēšana, lai optimizētu resursu, piemēram, slimnīcu gultu, medicīnas personāla un aprīkojuma, piešķiršanu. Tas ir ļoti svarīgi, lai uzlabotu pacientu aprūpi, samazinātu gaidīšanas laiku un efektīvi pārvaldītu izmaksas.
- Ražošanas procesa optimizācija : Lineārā programmēšana tiek izmantota, lai noteiktu optimālos ražošanas līmeņus vairākiem produktiem ražotnē, ņemot vērā tādus ierobežojumus kā darbaspēks, materiāli un iekārtu pieejamība.
- Lauksaimniecības plānošana : Lauksaimnieki un lauksaimniecības plānotāji izmanto lineāro programmēšanu, lai izlemtu par kultūraugu izvēli, zemes izmantošanu un resursu piešķiršanu, lai palielinātu ražu un peļņu, vienlaikus saglabājot resursus.
- Aviokompānijas apkalpes plānošana : Aviokompānijas izmanto lineāru programmu, lai efektīvi plānotu apkalpes, nodrošinot, ka lidojumos tiek nodrošināts personāls atbilstoši noteikumiem un līdz minimumam samazinot darbības izmaksas.
Šīs lietojumprogrammas demonstrē lineārās programmēšanas daudzpusību un jaudu, risinot sarežģītas optimizācijas problēmas dažādās nozarēs, parādot tās nozīmi mūsdienu uz datiem balstītajā pasaulē.
Lineārā programmēšana operāciju izpētē
- Galvenais rīks : Lineārā programmēšana ir pamatrīks operāciju izpētē resursu optimizēšanai.
- Lēmumu pieņemšana : palīdz pieņemt labākos lēmumus attiecībā uz resursu piešķiršanu, peļņas palielināšanu vai izmaksu samazināšanu.
- Plašas lietojumprogrammas : izmanto dažādās jomās, piemēram, loģistikā, ražošanā, finansēs un veselības aprūpē sarežģītu problēmu risināšanai.
- Reālās pasaules problēmu modelēšana : pārveido reālās pasaules problēmas matemātiskajos modeļos, lai atrastu visefektīvākos risinājumus.
Simpleksā metode
- Optimizācijas algoritms : Simpleksā metode ir spēcīgs algoritms, ko izmanto lineārajā programmēšanā, lai atrastu optimālo risinājumu lineārajām nevienādībām.
- Soli pa solim pieeja : tas iteratīvi virzās uz labāko risinājumu, pārvietojoties pa iespējamā reģiona malām, ko nosaka ierobežojumi.
- Efektivitāte : pazīstama ar savu efektivitāti liela mēroga lineārās programmēšanas problēmu risināšanā.
- Daudzpusība : piemērojams dažādās jomās, piemēram, uztura plānošanā, tīkla plūsmās, ražošanas plānošanā un citās jomās, demonstrējot tā daudzpusību.
Lineārā programmēšana – FAQ
Kas ir lineārā programmēšana?
Lineārā programmēšana ir matemātiska koncepcija, ko izmanto, lai optimizētu noteiktu lineāru problēmu, kurai ir dažādi ierobežojumi. Izmantojot lineāro programmēšanu, mēs iegūstam dotās problēmas optimālo izvadi
Kas ir lineārās programmēšanas problēmas?
Lineārās programmēšanas problēmas (LPP) ir problēmas, kas dod optimālu risinājumu dotajiem nosacījumiem.
Kas ir lineārās programmēšanas formula?
Vispārējās lineārās programmēšanas formulas ir,
- Mērķa funkcija: Z = cirvis + by
- Ierobežojumi: px + qy ≤ r, sx + ty ≤ u
- Nenegatīvi ierobežojumi: x ≥ 0, y ≥ 0
Kādi ir dažādi lineārās programmēšanas veidi?
Dažāda veida lineārās programmēšanas metodes ir,
- Lineārā programmēšana ar vienkāršās metodes palīdzību
- Lineārā programmēšana pēc R metodes
- Lineārā programmēšana ar grafisko metodi
Kādas ir lineārās programmēšanas prasības?
Lineārās programmēšanas problēmas ir dažādas prasības,
- Linearitāte
- Mērķa funkcija
- Ierobežojumi
- Nenegatīvisms
Kādas ir lineārās programmēšanas priekšrocības?
Lineārās programmēšanas priekšrocības ir dažādas:
- Tas nodrošina optimālu risinājumu jebkurai lineārai problēmai.
- Tas ir viegli lietojams un vienmēr nodrošina konsekventus rezultātus
- Tas palīdz palielināt peļņu un samazināt ieguldījumu izmaksas.