Garums, platums un augstums ir ģeometriskas figūras izmēri, kas norāda figūras garumu, platumu un augstumu. Garums, platums un augstums ir svarīgi rīki ģeometriskām figūrām.
Šajā rakstā jūs uzzināsit visas detaļas, kas saistītas ar garumu, platumu un augstumu. Ja esat īsts students un vēlaties uzzināt garumu, platumu un augstumu, tad esat īstajā vietā.
Satura rādītājs
- Kas ir garums platums augstums?
- Kā uzrakstīt garuma izmērus platumu un augstumu
- Garums × platums × augstums
- Garums pret platumu
- Garums, platums un augstums taisnstūrī
- Garuma platuma augstuma formula
Kas ir garums platums augstums?
Garums, platums un augstums tiek izmantoti, lai atrastu objekta malu vai izmērus. Figūras garākā mala ir garums, platums ir figūras īsākā mala, un figūras vertikālo izmēru sauc par augstumu. Garums un platums tiek izmantoti divdimensiju formās (2D formas), savukārt trīsdimensiju formās (3D formās) mēs izmantojam augstumu kopā ar garumu un platumu.
Garums
Rīks, kuram nepieciešams izmērīt attālumu starp diviem punktiem, ir pazīstams kā garums. Garumu izmanto, lai izmērītu figūras garāko izmēru. Garums ir lineārs mērījums, ko izmanto, lai izmērītu tikai attālumu, kas atdala divus punktus. Garuma mērvienības ir metri, kilometri, centimetri, collas utt.
Kā garuma piemēru varam teikt, ka kriketa laukuma laukuma garums ir 20 metri.
Platums
Rīku, ko izmanto, lai izmērītu mazāku attālumu līdz objektam vai figūrai, sauc par platumu. Tā ir figūras īsākā dimensija. Platums ir lineārs mērījums, ko izmanto, lai izmērītu tikai īsāku attālumu līdz objektam. Platuma mērvienības ir metri, kilometri, centimetri, collas un tā tālāk.
Kā platuma piemēru varam teikt, ka kriketa laukuma laukuma platums ir 5 metri garš.
Augstums
Vēl viens augstuma termins ir dziļums. Augstums vai dziļums ir trešā objekta vertikālā dimensija 3D formā. Tas nosaka objekta dziļumu vai augstumu. Augstuma mērvienības ir metri, kilometri, centimetri, collas un tā tālāk.
Kā uzrakstīt garuma izmērus platumu un augstumu
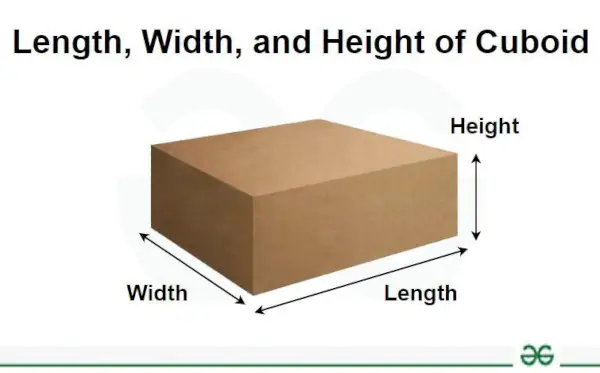
Garuma, platuma un augstuma izmērus var ierakstīt ļoti viegli, jo mēs jau esam izlasījuši šo rīku definīciju. 2D ģeometriskā formā mēs iegūstam tikai divus izmērus, garumu un platumu (platumu). 3D formā mēs iegūstam visus trīs garuma, platuma un augstuma izmērus. Attēla garākā puse ir marķēta kā garums. Vertikālais izmērs tiek rakstīts kā augstums vai dziļums. Atlikušo pusi sauc par platumu vai platumu.
Šī koncepcija ir parādīta iepriekš redzamajā diagrammā. Šo izmēru vienības ir izteiktas tādās vienībās kā metri, centimetri, collas utt.
Garums × platums × augstums
Sareizinot visas trīs dimensijas kopā, iegūstam ģeometriskas formas tilpumu. Tilpums tiek definēts kā vietas daudzums, ko aizņem ģeometriska forma. The kuboīda tilpums ir vienāds ar tā garuma, platuma un augstuma reizinājumu. Citiem vārdiem sakot, ja mēs reizinām visas trīs dimensijas kopā, mēs iegūstam kuboīda vai jebkura taisnstūra kastes tilpumu.
Matemātiski taisnstūra prizmas tilpums ( kuboīds ) vai kaste = garums × platums × augstums.
Piemēram, ja taisnstūra prizmas garums, platums un augstums ir attiecīgi 5, 8 un 10 vienības, tad tās tilpums (V) ir,
V = 5 × 8 × 10
V = 400 kuba vienības
Garums pret platumu
Gan garumu, gan platumu izmanto, lai izmērītu attālumu vai malas izmēru, taču starp šiem diviem ir ievērojama atšķirība. Garums ir garākais izmērs, bet platums ir īsākais izmērs. Garums vienmēr ir lielāks par platumu. Citiem vārdiem sakot, garums apzīmē figūras garāko pusi, bet platums apzīmē tās īsāko pusi. Platums (platums) piešķir ģeometriskas formas plašo raksturu, savukārt garums norāda, cik gara ir forma.
Ja ir doti divi ģeometriskas formas izmēri, kas ir attiecīgi 100 cm un 70 cm, tad mēs varam viegli teikt, ka 100 cm ir garums un 70 cm ir platums.
Garums, platums un augstums taisnstūrī
Taisnstūris ir 2D formas piemērs, tāpēc tam ir tikai garums un platums, bet taisnstūrveida kaste vai taisnstūrveida prizma (kuboīds) ir 3D forma, lai tam būtu visas trīs dimensijas: garums, platums un augstums. Tātad, mēs varam teikt, ka taisnstūra formas paplašinājumi 3D satur garumu, platumu un augstumu.
Garuma platuma augstuma formula
Garums, platums un augstums tiek izmantoti, lai aprēķinātu taisnstūra prizmas tilpumu un virsmas laukumu, izmantojot noteiktas formulas. Šīs formulas ir norādītas zemāk,
Taisnstūra prizmas tilpums Formula
Taisnstūra prizmas tilpums = garums × platums × augstums
Taisnstūra prizmas virsmas laukums Formula
Taisnstūra prizmas sānu virsmas laukums = 2 [(garums × platums) + (platums × augstums)]
Taisnstūra prizmas kopējais virsmas laukums = 2 [(garums × platums) + (platums × augstums) + (garums × augstums)]
Garums Platums Kastes augstums
Kastes garumu, platumu un augstumu var viegli izteikt, aplūkojot tās formu. Tā kā mēs zinām, ka kastes garums parasti ir garākā mala, tās platums ir īsākā mala un augstums ir dimensijas vertikālā dimensijā.

Parasti jebkuras 3-D formas izmēri tiek rakstīti kā garums, kam seko platums vai platums un augstums. Tas nozīmē, ka, ja ir jāmēra kastes izmēri, tad tie jānorāda kā garums, platums un augstums. Piemēram, 10 metri, 5 metri un 8 metri apzīmē,
- Kastes garums = 10 metri
- Kastes platums = 5 metri
- Kastes augstums = 8 metri
Līdzīgi raksti,
- 2D formu apgabals
- 3D formu virsmas laukums un apjoms
Garums Platums Augstums Piemēri
Daži piemēri par garuma, platuma un augstuma tēmu ir,
1. piemērs: 2D taisnstūra dārza izmēri ir 50 metri un 35 metri. Kāds ir garums un platums?
Risinājums:
Kā mēs zinām,
Garāks izmērs parasti tiek uzskatīts par garumu, bet īsāks par platumu
Garuma izmērs ir 50 metri un platums ir 35 metri
2. piemērs: ja taisnstūra kastes izmēri ir attiecīgi 26 m, 22 m un 24 m. Kāda būs šīs taisnstūra kastes augstuma vērtība?
Risinājums:
Kā zināms, izmēri 3D formā tiek izteikti garuma, platuma un augstuma secībā.
Dotie izmēri,
- Garums = 26 m
- Platums = 22 m
- Augstums = 24 m
Tātad, augstums ir 24 metri
3. piemērs: Taisnstūra prizmas garums, platums un augstums ir norādīti kā 6 cm, 4 cm un 5 cm. Nosakiet tā tilpumu.
ja vēl paziņojums java
Risinājums:
Ņemot vērā,
- Garums = 6 cm
- Platums = 4 cm
- Augstums = 5 cm
Tilpums = garums × platums × augstums
Tilpums = 6 × 4 × 5
Tilpums = 120 cm³
Prakses jautājumi par garumu platumu un augstumu
Daži prakses jautājumi par garumu, platumu un augstumu ir,
1. jautājums: atrodiet kuboīda tilpumu, kura garums, platums un augstums ir, garums = 12 cm, platums = 8 cm, augstums = 4 cm.
Q2: Atrodiet kuboīda tilpumu, kura garums, platums un augstums ir, garums = 18 m, platums = 9 m, augstums = 3 m.
3. jautājums: atrodiet kuboīda TSA, kura garums, platums un augstums ir, garums = 42 cm, platums = 28 cm, augstums = 14 cm.
4. jautājums: atrodiet taisnstūrveida LSA, kura garums, platums un augstums ir kā garums = 7 cm, platums = 5 cm, augstums = 6 cm.
Bieži uzdotie jautājumi par garuma platumu un augstumu
Kas ir garums platums augstums?
Garums, platums un augstums ir rīki, ko izmanto dažādu trīsdimensiju objektu izmēru mērīšanai.
Kurš ir garāks izmērs starp platumu un garumu?
Garums ir garāks izmērs. Garumu parasti izmanto objekta garāku izmēru mērīšanai.
Kas notiks ar dimensiju, ja objekts ir apaļš, piemēram, bumba?
Dažādiem objektu, piemēram, bumbiņu, mērījumiem mēs izmantojam rādiusu vai diametru, nevis garumu, platumu vai augstumu, ja objekts ir apaļš. Sfēras “augstums” ir vienāds ar tās diametru.
Tilpums vienmēr tiek aprēķināts pēc formulas garuma × platums × augums?
Tilpuma formula parasti ir garums × platums × augstums 3-D formām, kur tās izmēri ir garums, platums un augstums.
