Aritmētiskā vērtība, kas tiek izmantota daudzuma attēlošanai un tiek izmantota aprēķinos, ir definēta kā skaitļi. Simbols, piemēram, 4, 5, 6, kas apzīmē skaitli, ir pazīstams kā cipars. Bez skaitļiem mēs nevaram skaitīt lietas, datumu, laiku, naudu utt., šie skaitļi tiek izmantoti arī mērīšanai un marķēšanai.

Ciparu īpašības padara tos noderīgus, veicot aritmētiskās darbības ar tiem. Šos skaitļus var rakstīt ciparu formās un arī vārdos.

Piemēram , 3 ir rakstīts kā trīs ar vārdiem, 35 ir rakstīts kā trīsdesmit pieci vārdos utt. Lai uzzinātu vairāk, skolēni var rakstīt skaitļus no 1 līdz 100 vārdos.

Ir dažādi skaitļu veidi, kurus mēs varam iemācīties. Tie ir veseli un naturāli skaitļi, nepāra un pāra skaitļi, racionāli un iracionāli skaitļi utt.

Kas ir skaitļu sistēma?

Skaitļu sistēma ir skaitļu parādīšanas metode, rakstot, kas ir matemātisks veids, kā attēlot dotās kopas skaitļus, izmantojot skaitļus vai simbolus matemātiskā veidā. Rakstīšanas sistēma skaitļu apzīmēšanai, loģiskā veidā izmantojot ciparus vai simbolus, ir definēta kā skaitļu sistēma.

Mēs varam izmantot ciparus no 0 līdz 9, lai veidotu visus skaitļus. Ar šiem cipariem ikviens var izveidot bezgalīgus skaitļus.

Piemēram, 156, 3907, 3456, 1298, 784859 utt.

Kas ir kvadrātsakne?

Kvadrātsakņu skaita vērtība, kas, reizinot ar sevi, dod sākotnējo skaitli. Pieņemsim, ka a ir kvadrātsakne no b, tad tā tiek attēlota kā a = √b vai mēs varam izteikt to pašu vienādojumu kā a2 = b. Šeit “√” šis simbols, ko izmantojām, lai attēlotu skaitļu sakni, tiek saukts par radikālu. Pozitīvais skaitlis, ja tas jāreizina ar sevi, ir skaitļa kvadrāts. Jebkura pozitīva skaitļa kvadrāta kvadrātsakne dod sākotnējo skaitli.

Piemēram, kvadrāts 4 ir 16, 4²= 16, un kvadrātsakne no 16, √16 = 4. Tā kā 4 ir ideāls kvadrāts, tāpēc ir viegli atrast šādu skaitļu kvadrātsakni, taču nepilnīga kvadrāta gadījumā tas ir ļoti sarežģīti.

Kvadrātsakne ir attēlota kā '√' To sauc par radikālu simbolu. Lai attēlotu skaitli “a” kā kvadrātsakni, izmantojot šo simbolu, var rakstīt šādi: “√a”, kur a ir skaitlis.

parametrs čaulas skriptā

Skaitlis šeit zem radikālas simbola tiek saukts par radikānu. Piemēram, kvadrātsakne no 4 tiek attēlota arī kā 4 radikālis. Abi apzīmē vienu un to pašu vērtību.

Kvadrātsaknes atrašanas formula ir šāda: a = √b

Kvadrātsakņu īpašības

To definē kā funkciju “viens pret vienu”, kas kā ievadi izmanto pozitīvu skaitli un atgriež kvadrātsakni no dotā ievades skaitļa.

f(x) = √x

Piemēram, ja x = 9, tad funkcija atgriež izvades vērtību kā 3.

datortīkli

Kvadrātsaknes īpašības ir šādas:

• Ja skaitlis ir ideāls kvadrātveida skaitlis, tad noteikti pastāv perfekta kvadrātsakne.
• Ja skaitlis beidzas ar pāra skaitu nullēm (0), tad mums var būt kvadrātsakne.
• Abas kvadrātsaknes vērtības var reizināt. Piemēram, √3 var reizināt ar √2, tad rezultāts būs √6.
• Sareizinot divas vienādas kvadrātsaknes, rezultātam jābūt radikālam skaitlim. Tas parāda, ka rezultāts ir skaitlis, kas nav kvadrātsakne. Piemēram, ja √7 reizina ar √7, iegūtais rezultāts ir 7.
• Negatīvo skaitļu kvadrātsakne nav definēta. Tādējādi ideāls kvadrāts nevar būt negatīvs.
• Daži skaitļi beidzas ar 2, 3, 7 vai 8 (vienības ciparā), tad ideālā kvadrātsakne nepastāv.
• Daži skaitļi vienības ciparā beidzas ar 1, 4, 5, 6 vai 9, tad skaitlim būs kvadrātsakne.

Ir viegli atrast kvadrātsakni no skaitļa, kas ir ideāls kvadrāts.

Ideāli kvadrāti ir tie pozitīvie skaitļi, kurus var uzrakstīt kā skaitļa reizinājumu ar sevi, vai arī jūs varat teikt, ka ideāls kvadrāts ir skaitlis, kas ir jebkura vesela skaitļa jaudas 2 vērtība.

Skaitlis, ko var izteikt kā divu vienādu veselu skaitļu reizinājumu. Piemēram, 16 ir ideāls kvadrāts, jo tas ir divu vienādu veselu skaitļu reizinājums, 4 × 4 = 16. Tomēr 24 nav ideāls kvadrāts, jo to nevar izteikt kā divu vienādu veselu skaitļu reizinājumu. (8 × 3 = 24).

Skaitli, ko iegūst, izliekot veselu skaitli kvadrātā, sauc par perfektu kvadrātu.

Ja pieņemam, ka N ir pilnīgs vesela skaitļa y kvadrāts, to var uzrakstīt kā N = y un y = y reizinājums².

Tātad ideālo kvadrātveida formulu var izteikt šādi:

N = Y ²

Izmantosim formulu ar vērtībām:

Ja y = 9 un N = y²

kas ir svn checkout

Tas nozīmē, ka N = 9²= 81.

Šeit 81 ir ideāls kvadrāts ar 9, jo tas ir vesela skaitļa kvadrāts.

Ar kvadrātsakņu palīdzību mēs varam noteikt, vai skaitlis ir ideāls kvadrāts, ja mēs aprēķinām dotā skaitļa kvadrātsakni.

Ja kvadrātsakne ir vesels skaitlis, tad dotais skaitlis būs ideāls kvadrāts, un, ja kvadrātsaknes vērtība nav vesels skaitlis, tad dotais skaitlis nav ideāls kvadrāts.

Piemēram, lai pārbaudītu, vai 24 ir ideāls kvadrāts, mēs aprēķināsim tā kvadrātsakni. √24 = 4,898979. Kā redzam, 4,898979 nav vesels skaitlis, tāpēc 24 nav ideāls kvadrāts.

Ņemsim vēl vienu piemēru

Skaitlis 49. √49 = 7. Var redzēt, ka 7 ir vesels skaitlis, tāpēc 49 ir ​​ideāls kvadrāts.

Vai 196 ir ideāls laukums?

Risinājums:

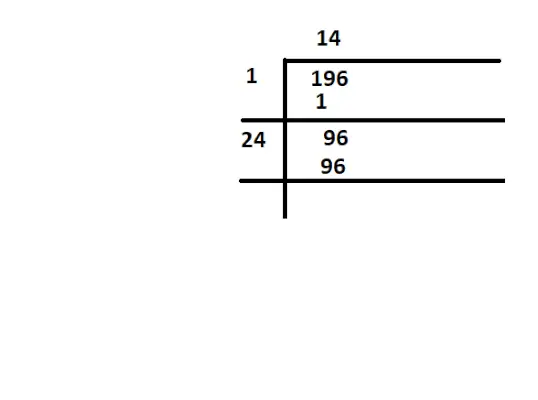
Lai pārbaudītu, vai 196 ir ideāls kvadrāts, mums jāatrod kvadrātsaknes no 196

java slēdža paziņojums

ideāls kvadrāts no 196

Šeit kvadrātsakne no 196 ir 14

Perfektie kvadrāti ir tie pozitīvie skaitļi, kurus var uzrakstīt kā skaitļa reizinājumu ar sevi, vai arī jūs varat teikt, ka ideāls kvadrāts ir skaitlis, kas ir jebkura vesela skaitļa jaudas 2 vērtība.

Šeit mēs varam ierakstīt √196 = 14 vai 14²= 14 × 14 = 196.

Tāpēc 196 ir ideāls kvadrāts.

Līdzīgi jautājumi

1. jautājums: kāda ir kvadrātsakne no 625?

Risinājums:

ideāls kvadrāts no 625

javascript nolaižamā izvēlne

šeit 625 ir ideāls kvadrāts no 25

Tātad mēs varam rakstīt kā √625 = 25 vai 25²= 25 × 25 = 625

2. jautājums: kā atrast kvadrātsakni no 24?

Risinājums:

kvadrātsakne no 24

Šeit 24 nav ideāls kvadrāts 4,8989.

Tāpēc √24 = 4,8989...

3. jautājums: atrast kvadrātsakni no 361?

Risinājums:

361 kvadrāts

Šeit kvadrātsakne no 361 ir 19 , vesels skaitlis, kas ir ideāls kvadrāts

Tāpēc √361 = 19 vai 19²= 19 × 19 = 361