Trijstūri ir trīspusēji slēgti daudzstūri, ko veido trīs līniju krustošanās. Ikdienā ar to sastopas daudz. Tā ir viena no ģeometrijas pamatformām. Tam ir trīs malas, trīs leņķi un trīs virsotnes. Taisnleņķa trijstūris ir tāds, kurā viens no leņķiem vienmēr ir vienāds ar 90°. Pitagora teorēma ir atvasināts taisnleņķa trijstūriem, kas nosaka, ka hipotenūzas kvadrāts (garākā mala) ir vienāds ar pamatnes un perpendikulāra kvadrātu summu.

Ņemot vērā vismaz divu taisnleņķa trijstūra malu garumu, mēs varam atrast jebkura taisnleņķa trijstūra leņķa vērtību. Šim nolūkam mēs izmantojam dažādas trigonometriskās funkcijas, piemēram, sinusu, kosinusu, tangensu, kotangensu, sek un koseku. Tie palīdz mums saistīt taisnleņķa trīsstūra leņķus ar tā malām.

Īpašības

• Starp trim virsotnēm ir taisnleņķa virsotne
• Malu, kas ir pretēja taisnleņķa virsotnei, sauc par hipotenūza .
• Sānu garums atbilst Pitagora teorēmai, kas nosaka

hipotenūza ² = bāze ² + augstums virs jūras līmeņa ²

• Hipotenūza ir taisnleņķa trīsstūra garākā mala.
• Leņķi, kas nav taisnais leņķis, ir asi leņķi, jo vērtība ir mazāka par 90^O

Trigonometriskās funkcijas

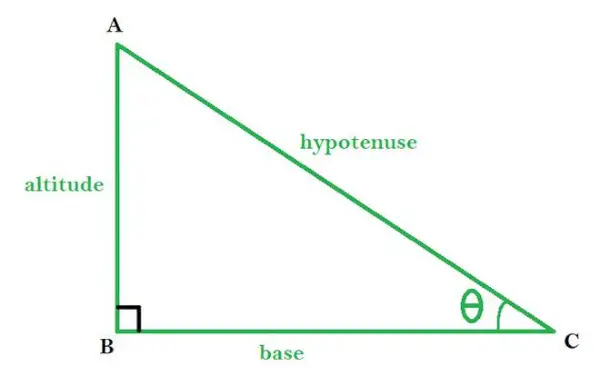
ABC ir taisnleņķa trīsstūris ar ∠B kā taisnleņķi

inurl:.git/head

• cosθ: Tas dod taisnleņķa trijstūra pamatnes attiecību ar hipotenūzu.

cosθ = bāze / hipotenūza

• grēksθ: Tas parāda augstuma attiecību ar taisnleņķa trīsstūra hipotenūzu.

sinθ = augstums / hipotenūza

• tanθ: Tā ir augstuma attiecība pret taisnleņķa trijstūra pamatni.

tanθ = augstums / bāze

• cotθ: Tā ir tanθ apgrieztā vērtība
• secθ: Tā ir cosθ apgrieztā vērtība
• cosecθ: Tā ir sinθ apgrieztā vērtība

Lai atrastu taisnleņķa trijstūra leņķus, mēs varam ņemt trigonometrisko apgriezto trijstūra doto malu attiecību.

Piemērs:

Ja sinθ = x, tad mēs varam rakstīt

θ = grēks ^-1 x.

Tas atgriež leņķi, kuram leņķa sinusa vērtība ir x.

Tāpat pastāv cos^-1θ, tātad^-1es, gultiņa^-1θ, sek^-1θ un cosec^-1i

Problēmu paraugi

1. jautājums. Dots taisnleņķa trīsstūris, kura pamatne ir 10 cm un hipotenūza ir 20 cm. Atrodiet bāzes leņķa vērtību.

Risinājums:

Ņemot vērā, pamatne = 10 cm

Hipotenūza = 20 cm

Pieņemsim, ka bāzes leņķa vērtība ir θ. Mēs varam rakstīt

cosθ = bāze / hipotenūza = 10/20 = 1/2

θ = cos^-1(1/2) = 60^O

Tādējādi bāzes leņķa vērtība ir 60 ^O .

2. jautājums. Atrodiet taisnleņķa trijstūra leņķu vērtību, ja viens no asajiem leņķiem ir divreiz lielāks par otru.

Risinājums:

Tā kā mēs zinām, ka visu trīs trijstūra leņķu summa ir 180^O.

Tā kā viens no leņķiem ir 90^Oun viens no asajiem leņķiem ir divreiz par otru, mēs tos varam uzskatīt par θ un 2θ.

Tātad, mēs varam rakstīt

90^O+ θ + 2θ = 180^O

3θ = 180^O– 90^O

3θ = 90^O

θ = 90^O/3 = 30 ^O

2θ = 2 × 30^O= 60 ^O

Tātad leņķi ir 30 ^O , 60 ^O , un 90 ^O .

3. jautājums. Atrodiet 5m garu kāpņu pacēluma leņķa vērtību, ņemot vērā, ka kāpņu pamatne atrodas 3m attālumā no sienas.

Risinājums:

Tā kā kāpnes darbojas kā taisnleņķa trijstūra hipotenūza un pamatnes attālums ir vienāds ar 3 m, mēs varam rakstīt

Hipotenūza = 5m

Pamatne = 3m

Ļaujiet pacēluma leņķim būt θ. Tātad, mēs varam rakstīt

cosθ = Bāze / Hipotenūza = 3/5

θ = cos^-1(3/5)

θ = 53^O

Tādējādi pacēluma leņķa vērtība ir 53^O.

4. jautājums. Atrodiet hipotenūzas vērtību, ja augstuma garums ir 8 m un bāzes leņķis ir vienāds ar 30 ^O .

Risinājums:

Ņemot vērā, bāzes leņķis ir vienāds ar 30^Oun augstums ir vienāds ar 8 m, mēs varam izmantot sinusa funkciju, lai atrastu hipotenūzas garumu.

grēks30 ^O = augstums / hipotenūza

hipotenūza = augstums / grēks30^O

Kopš grēka vērtības30^Oir vienāds ar 1/2, mēs varam rakstīt

hipotenūza = augstums / (1/2) = 2 × augstums

Tādējādi hipotenūza = 2 × 8 = 16 m

Tādējādi hipotenūzas garums ir vienāds ar 16 m.