Ford-Fulkerson algoritms ir plaši izmantots algoritms, lai atrisinātu maksimālās plūsmas problēmu plūsmas tīklā. Maksimālās plūsmas problēma ietver maksimālā plūsmas daudzuma noteikšanu, ko var nosūtīt no avota virsotnes uz izlietnes virsotni virzītā svērtā grafikā, ņemot vērā kapacitātes ierobežojumus malās.
Algoritms darbojas, iteratīvi atrodot palielināšanas ceļu, kas ir ceļš no avota līdz izlietnei atlikušajā grafikā, t.i., grafiks, kas iegūts, atņemot strāvas plūsmu no katras malas jaudas. Pēc tam algoritms palielina plūsmu pa šo ceļu par maksimāli iespējamo summu, kas ir malu minimālā ietilpība gar ceļu.
Problēma:
Dots grafiks, kas attēlo plūsmas tīklu, kurā katrai malai ir jauda. Tāpat, ņemot vērā divas virsotnes avots 'smiltis izlietne “t” grafikā atrodiet maksimālo iespējamo plūsmu no s līdz t ar šādiem ierobežojumiem:
- Plūsma uz malas nepārsniedz doto malas kapacitāti.
- Ienākošā plūsma ir vienāda ar izejošo plūsmu katrai virsotnei, izņemot s un t.
Piemēram, apsveriet šādu grafiku no CLRS grāmatas.
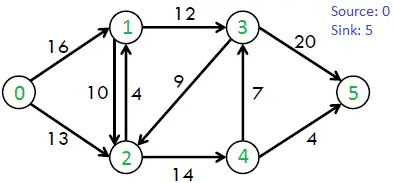
Maksimālā iespējamā plūsma iepriekš minētajā grafikā ir 23.

Priekšnosacījums: Maksimālās plūsmas problēmas ievads
Ford-Fulkersona algoritms
Tālāk ir sniegta vienkārša Ford-Fulkersona algoritma ideja:
- Sāciet ar sākotnējo plūsmu kā 0.
- Lai gan pastāv papildu ceļš no avota līdz izlietnei:
- Atrodiet papildinošu ceļu, izmantojot jebkuru ceļa meklēšanas algoritmu, piemēram, meklēšanu pēc platuma vai meklēšanu pēc dziļuma.
- Nosakiet plūsmas daudzumu, ko var nosūtīt pa palielināšanas ceļu, kas ir minimālā atlikušā jauda gar ceļa malām.
- Palieliniet plūsmu pa palielināšanas ceļu par noteikto daudzumu.
- Atgrieziet maksimālo plūsmu.
Laika sarežģītība: Iepriekš minētā algoritma laika sarežģītība ir O(max_flow * E). Mēs veicam cilpu, kamēr ir palielināšanas ceļš. Sliktākajā gadījumā mēs varam pievienot 1 plūsmas vienību katrā iterācijā. Tāpēc laika sarežģītība kļūst par O(max_flow * E).
Kā ieviest iepriekš minēto vienkāršo algoritmu?
Vispirms definēsim atlikušā grafika jēdzienu, kas ir nepieciešams ieviešanas izpratnei.
Atlikušais grafiks Plūsmas tīkls ir grafiks, kas norāda papildu iespējamo plūsmu. Ja atlikušajā grafikā ir ceļš no avota līdz izlietnei, tad ir iespējams pievienot plūsmu. Katrai atlikušā grafika malai ir vērtība, ko sauc atlikušā jauda kas ir vienāda ar malas sākotnējo jaudu mīnus strāvas plūsma. Atlikusī jauda būtībā ir malas pašreizējā jauda.
Tagad parunāsim par ieviešanas detaļām. Atlikušā ietilpība ir 0, ja starp divām atlikušā grafa virsotnēm nav malas. Mēs varam inicializēt atlikušo grafiku kā sākotnējo grafiku, jo nav sākotnējās plūsmas un sākotnēji atlikušā jauda ir vienāda ar sākotnējo jaudu. Lai atrastu papildināšanas ceļu, mēs varam veikt atlikušā grafika BFS vai DFS. Mēs esam izmantojuši BFS tālāk norādītajā ieviešanā. Izmantojot BFS, mēs varam noskaidrot, vai ir ceļš no avota līdz izlietnei. BFS veido arī vecāku [] masīvu. Izmantojot vecāku [] masīvu, mēs šķērsojam atrasto ceļu un atrodam iespējamo plūsmu pa šo ceļu, atrodot minimālo atlikušo jaudu gar ceļu. Vēlāk mēs pievienojam atrastā ceļa plūsmu kopējai plūsmai.
2 līdz 1 multipleksors
Svarīgi ir tas, ka mums ir jāatjaunina atlikušās jaudas atlikušajā grafikā. Mēs atņemam ceļa plūsmu no visām ceļa malām un pievienojam ceļa plūsmu gar reversajām malām. Mums ir jāpievieno ceļa plūsma gar pretējām malām, jo vēlāk var būt nepieciešams nosūtīt plūsmu pretējā virzienā (skatiet, piemēram, šo saiti).
Zemāk ir Ford-Fulkerson algoritma ieviešana. Lai lietas būtu vienkāršas, grafiks tiek attēlots kā 2D matrica.
C++
// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> >'t' in residual graph. Also fills parent[] to store the> >path */> bool> bfs(>int> rGraph[V][V],>int> s,>int> t,>int> parent[])> {> >// Create a visited array and mark all vertices as not> >// visited> >bool> visited[V];> >memset>(visited, 0,>sizeof>(visited));> >// Create a queue, enqueue source vertex and mark source> >// vertex as visited> >queue<>int>>q;> >q.push(s);> >visited[s] =>true>;> >parent[s] = -1;> >// Standard BFS Loop> >while> (!q.empty()) {> >int> u = q.front();> >q.pop();> >for> (>int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Ja mēs atrodam savienojumu ar izlietnes mezglu, // tad BFS vairs nav jēgas. Mums // vienkārši jāiestata tā vecākais un var atgriezties // true if (v == t) { vecāks[ v] = u; atgriezt patiesu; } q.push(v); vecāks[v] = u; apmeklēts[v] = patiess; } } } // Mēs nesasniedzām izlietni BFS, sākot no avota, tāpēc // return false return false; } // Atgriež maksimālo plūsmu no s uz t dotajā grafikā int fordFulkerson(int graph[V][V], int s, int t) { int u, v; // Izveidojiet atlikušo grafiku un aizpildiet atlikušo grafiku // ar dotajām kapacitātēm sākotnējā grafikā kā // atlikušās kapacitātes atlikušajā grafikā int rGrafs[V] [V]; // Atlikušais grafs kur rGraph[i][j] // norāda malas atlikušo kapacitāti // no i līdz j (ja ir mala. Ja // rGraph[i][j] ir 0, tad nav) for (u = 0; u for (v = 0; v rGrafs[u][v] = grafiks[u][v]; int vecāks[V]; // Šo masīvu aizpilda BFS un // saglabāt ceļu int max_flow = 0 // Sākotnēji nav plūsmas // Palielināt plūsmu, kamēr ir ceļš no avota līdz // grimt while (bfs(rGraph, s, t, parent)) { // Atrast malu minimālo atlikušo ietilpību; pa // ceļu, ko aizpilda BFS, vai arī mēs varam teikt, ka atrodam // maksimālo plūsmu cauri atrastajam ceļam vecāks[v]; ceļš_plūsma = min(ceļš_plūsma, rGrafs[u][v] } // atjaunina malu atlikušās kapacitātes un // apgrieztās malas, kas paredzētas (v = t; v != s; v =); mātes[v]) { u = mātes_plūsma [v] - = ceļš rGrafs [v][u] += ceļa_plūsma } // Pievienot ceļa plūsmu kopējai plūsmai; // Atgriezt kopējo plūsmu return max_flow; } // Draivera programma, lai pārbaudītu iepriekš minētās funkcijas int main() { // Izveidosim grafiku, kas parādīts iepriekš minētajā piemērā int graph[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0} }; cout<< 'The maximum possible flow is ' << fordFulkerson(graph, 0, 5); return 0; }> |
>
>
Java
Aktieris Reha
// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> >static> final> int> V =>6>;>// Number of vertices in graph> >/* Returns true if there is a path from source 's' to> >sink 't' in residual graph. Also fills parent[] to> >store the path */> >boolean> bfs(>int> rGraph[][],>int> s,>int> t,>int> parent[])> >{> >// Create a visited array and mark all vertices as> >// not visited> >boolean> visited[] =>new> boolean>[V];> >for> (>int> i =>0>; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Ja mēs atrodam savienojumu ar izlietni // mezglu, tad BFS vairs nav jēgas // Mums tikai jāiestata tā vecāk // un var atgriezt patiesu if (v == t) { vecāks[ v] = u; atgriezt patiesu; } rinda.pievienot(v); vecāks[v] = u; apmeklēts[v] = patiess; } } } // Mēs nesasniedzām izlietni BFS, sākot no avota, // tāpēc return false return false; } // Atgriež maksimālo plūsmu no s uz t dotajā // grafikā int fordFulkerson(int graph[][], int s, int t) { int u, v; // Izveidojiet atlikušo grafiku un aizpildiet atlikušo // grafiku ar dotajām ietilpībām sākotnējā grafikā // kā atlikušās kapacitātes atlikušajā grafikā // Atlikušais grafiks, kur rGraph[i][j] norāda // malas atlikušo kapacitāti no i līdz j (ja // ir mala. Ja rGrafs[i][j] ir 0, tad // nav) int rGrafs[][] = new int[V][V]; for (u = 0; u for (v = 0; v rGrafs[u][v] = grafiks[u][v]; // Šo masīvu aizpilda BFS un saglabāt ceļu int vecāk[] = new int[ V] int max_flow = 0 // Sākotnēji nav plūsmas // Palielināt plūsmu, kamēr ir ceļš no avota // līdz izlietnei, kamēr (bfs(rGraph, s, t, parent)) { // Atrast minimālo atlikušo jaudu; no malām // pa ceļu, ko piepilda BFS ]) { u = mātes [v] ceļa_plūsma = Math.min(ceļa_plūsma, rGrafs[u][v] } // atjaunināt malu un // apgriezto malu atlikušās ietilpības ceļā uz (v = t; v != s = mātes [v]) { u = vecāks[v] - rGrafs[v][u] += ceļa_plūsma } // Pievienot ceļu plūsmai; flow max_flow += path_flow } // Atgriež kopējo plūsmas atgriešanos max_flow } // Draiveris, lai pārbaudītu iepriekš minētās funkcijas public static void main(String[] args) izmet java.lang.Exception { // Izveidosim parādīto grafiku; iepriekš minētajā piemērā int grafiks[][] = jauns int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = jauns MaxFlow(); System.out.println('Maksimālā iespējamā plūsma ir ' + m.fordFulkerson(graph, 0, 5)); } }> |
>
>
Python
# Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> |
ievietošanas kārtošanas algoritms
>
>
C#
// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List |
>
>
imessage spēles Android ierīcēs
Javascript
> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // Ja mēs atrodam savienojumu ar izlietni // mezglu, tad BFS vairs nav jēgas // Mums tikai jāiestata tā vecāk // un var atgriezt patiesu if (v == t) { vecāks[ v] = u; atgriezt patiesu; } rinda.push(v); vecāks[v] = u; apmeklēts[v] = patiess; } } } // Mēs nesasniedzām izlietni BFS, sākot no // no avota, tāpēc return false return false; } // Atgriež maksimālo plūsmu no s uz t // dotajā grafika funkcijā fordFulkerson(graph, s, t) { let u, v; // Izveidojiet atlikušo grafiku un aizpildiet // atlikušo grafiku ar norādītajām ietilpībām // sākotnējā grafikā kā atlikumu // jaudas atlikušajā grafikā // Atlikušā diagramma kur rGraph[i][j] // norāda malas atlikušo kapacitāti // / no i līdz j (ja ir mala. // Ja rGraph[i][j] ir 0, tad nav // nav) lai rGraph = new Array(V); for(u = 0; u { rGrafs[u] = jauns masīvs(V); for(v = 0; v rGrafs[u][v] = grafiks[u][v]; } // Šo masīvu aizpilda BFS un saglabāt ceļu let parent = new Array(V) // Sākotnēji nav plūsmas let max_flow = 0 // Palielināt plūsmu, kamēr ir ceļš no avota līdz izlietnei, kamēr (bfs(rGraph, s, t); , vecāks)) { // Atrodiet malu minimālo atlikušo ietilpību // pa ceļu, ko aizpilda BFS ; v != s; apgrieztās malas pa ceļu for(v = t; v != s; v = vecāks[v]) { u = vecāks[v] - rGrafs[v][u] +; = ceļš_plūsma } // Pievienot ceļa plūsmu kopējai plūsmai. , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 , 20 ], [ 0, 0, 0, 7, 0, 4 ], [ 0, 0, 0, 0, 0, 0 ]]; document.write('Maksimālā iespējamā plūsma ir ' + fordFulkerson(graph, 0, 5)); // Šo kodu ir sagatavojis avanitrachhadiya2155>> |
>The maximum possible flow is 23>
Laika sarežģītība : O(|V| * E^2) ,kur E ir šķautņu skaits un V ir virsotņu skaits.
Telpas sarežģītība: O(V), kā mēs izveidojām rindu.
Iepriekš minēto Ford Fulkersona algoritma ieviešanu sauc Edmonda-Karpa algoritms . Edmonds-Karp ideja ir izmantot BFS Ford Fulkerson ieviešanā, jo BFS vienmēr izvēlas ceļu ar minimālu malu skaitu. Izmantojot BFS, sliktākā gadījuma laika sarežģītību var samazināt līdz O (VE2). Iepriekš minētajā implementācijā tiek izmantots blakus esošu matricas attēlojums, lai gan BFS izmanto O (V2) laikā, iepriekš minētās realizācijas laika sarežģītība ir O(EV3) (Atsaukties CLRS grāmata lai pierādītu laika sarežģītību)
Tā ir svarīga problēma, jo tā rodas daudzās praktiskās situācijās. Piemēri ietver transportēšanas maksimālu palielināšanu ar noteiktiem trafika ierobežojumiem, pakešu plūsmas maksimizēšanu datortīklos.
Dinc algoritms maksimālajai plūsmai.
Vingrinājums:
Modificējiet iepriekš minēto implementāciju, lai tā darbotos O (VE2) laiks.
