Dzēšanas funkcija tiek izmantota, lai dzēstu norādīto mezglu no binārā meklēšanas koka. Tomēr mums ir jāizdzēš mezgls no binārā meklēšanas koka tā, lai netiktu pārkāptas binārās meklēšanas koka īpašības. Ir trīs situācijas, kā dzēst mezglu no binārās meklēšanas koka.
avl koks
Dzēšamais mezgls ir lapas mezgls
Tas ir vienkāršākais gadījums, šajā gadījumā nomainiet lapas mezglu ar NULL un vienkārši atbrīvojiet piešķirto vietu.
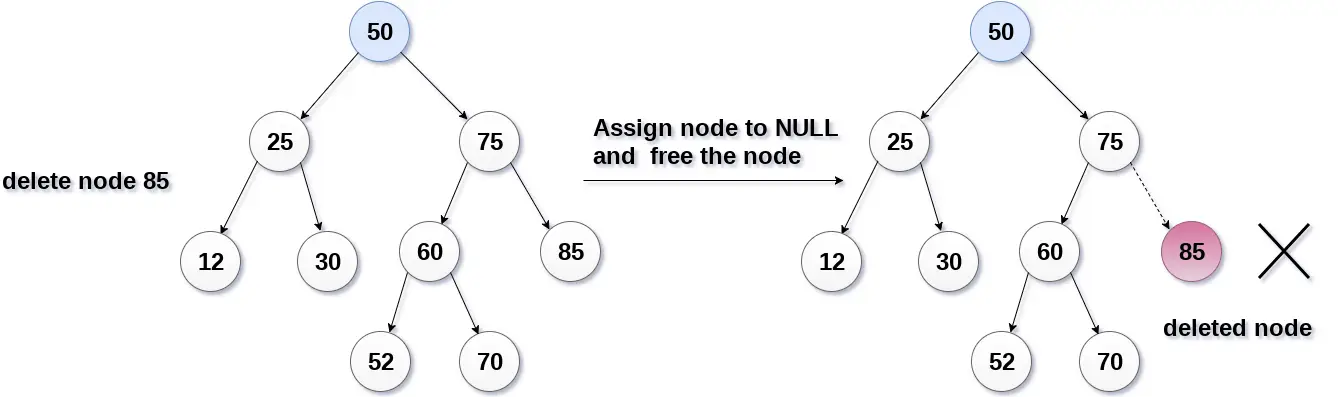
Nākamajā attēlā mēs dzēšam mezglu 85, jo mezgls ir lapas mezgls, tāpēc mezgls tiks aizstāts ar NULL un tiks atbrīvota piešķirtā vieta.
Dzēšamajam mezglam ir tikai viens bērns.
Šajā gadījumā nomainiet mezglu ar tā atvasināto mezglu un izdzēsiet pakārtoto mezglu, kurā tagad ir dzēšamā vērtība. Vienkārši nomainiet to ar NULL un atbrīvojiet piešķirto vietu.
numurs uz virkni java
Nākamajā attēlā mezgls 12 ir jāizdzēš. Tam ir tikai viens bērns. Mezgls tiks aizstāts ar tā atvasināto mezglu, un aizstātais mezgls 12 (kas tagad ir lapas mezgls) tiks vienkārši izdzēsts.

Dzēšamajam mezglam ir divi bērni.
Tas ir nedaudz sarežģīts gadījums, salīdzinot ar citiem diviem gadījumiem. Tomēr dzēšamais mezgls tiek rekursīvi aizstāts ar tā secības pēcteci vai priekšgājēju, līdz mezgla vērtība (jāizdzēš) tiek ievietota koka lapā. Pēc procedūras nomainiet mezglu ar NULL un atbrīvojiet piešķirto vietu.
Nākamajā attēlā ir jādzēš mezgls 50, kas ir koka saknes mezgls. Tālāk norādītā koka šķērsošana secībā.
numurs uz virkni java
6, 25, 30, 50, 52, 60, 70, 75.
aizstāt 50 ar tā kārtas pēcteci 52. Tagad 50 tiks pārvietoti uz koka lapu, kas tiks vienkārši dzēsta.

Algoritms
Dzēst (TREE, ITEM)
Ierakstiet “prece nav atrasta kokā” ELSE IF ITEM DATA
Dzēst(TREE->LEFT, ITEM)
CITĀJĀ, JA ITEM > KOKS -> DATI
Dzēst (KOKS —> LABĀJĀ, ITEM)
CITU JA KOKS -> KREISĀ UN KOKS -> LABAIS
IESTATĪT TEMP = atrastLielāko mezglu (KOKS -> PA kreisi)
SET TREE -> DATA = TEMP -> DATA
Dzēst (KOKS -> PA kreisi, TEMP. -> DATI)
CITS
SET TEMP = KOKS
IF TREE -> LEFT = NULL UN TREE -> RIGHT = NULL
IESTATĪT KOKU = NULL
ELSE IF TREE -> LEFT != NULL
IESTATĪT KOKU = TREE -> LEFT
CITS
IESTATĪT KOKU = KOKS -> LABĀ
[JA BEIGAS]
BEZMAKSAS TEMP
[JA BEIGAS]
Funkcija:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 