Šajā rakstā ir runāts par datu šifrēšanas standartu (DES), vēsturisku šifrēšanas algoritmu, kas pazīstams ar 56 bitu atslēgas garumu. Mēs izpētām tā darbību, atslēgu pārveidošanas un šifrēšanas procesu, atklājot tā lomu datu drošībā un ievainojamības mūsdienu kontekstā.
Kas ir DES?
Datu šifrēšanas standarts (DES) ir bloku šifrs ar 56 bitu atslēgas garumu, kam ir bijusi nozīmīga loma datu drošībā. . Datu šifrēšanas standarts (DES) ir atzīts par neaizsargātu pret ļoti spēcīgiem uzbrukumiem, tāpēc DES popularitāte ir nedaudz samazinājusies. DES ir bloku šifrs un šifrē datus blokos, kuru lielums ir 64 biti katrs, kas nozīmē, ka 64 biti vienkārša teksta tiek izmantoti kā ievade DES, kas rada 64 bitus šifrētā teksta. Tas pats algoritms un atslēga tiek izmantoti šifrēšanai un atšifrēšana , ar nelielām atšķirībām. Atslēgas garums ir 56 biti .
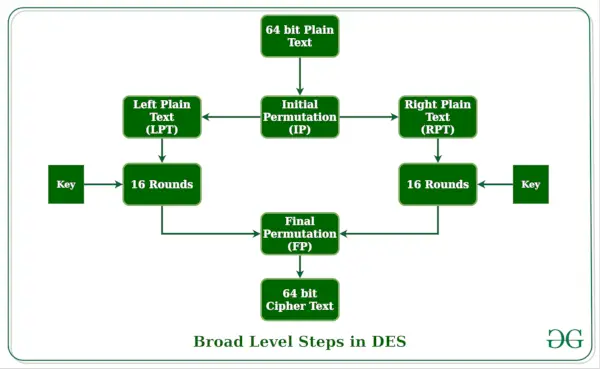
Pamatideja ir parādīta zemāk:
kāds ir mana monitora ekrāna izmērs
Mēs esam minējuši, ka DES izmanto 56 bitu atslēgu. Faktiski sākotnējā atslēga sastāv no 64 bitiem. Tomēr, pirms DES process pat sākas, katrs 8. atslēgas bits tiek izmests, lai izveidotu 56 bitu atslēgu. Tas nozīmē, ka bitu pozīcijas 8, 16, 24, 32, 40, 48, 56 un 64 tiek atmestas.

Tādējādi katra 8. atslēgas bita atmešana rada a 56 bitu atslēga no oriģināla 64 bitu atslēga .
DES ir balstīta uz diviem galvenajiem atribūtiem kriptogrāfija : aizstāšana (saukta arī par apjukumu) un transponēšana (saukta arī par difūziju). DES sastāv no 16 soļiem, no kuriem katru sauc par kārtu. Katrā kārtā tiek veiktas aizstāšanas un transponēšanas darbības. Tagad apspriedīsim DES plaša līmeņa darbības.
- Pirmajā darbībā 64 bitu vienkāršā teksta bloks tiek nodots iniciāļiem Permutācija (IP) funkcija.
- Sākotnējā permutācija tiek veikta vienkāršam tekstam.
- Pēc tam sākotnējā permutācija (IP) rada divas permutētā bloka puses; sakot kreiso vienkāršu tekstu (LPT) un labo vienkāršu tekstu (RPT).
- Tagad katrs LPT un RPT iziet cauri 16 šifrēšanas procesa posmiem.
- Galu galā LPT un RPT tiek atkārtoti apvienoti, un apvienotajam blokam tiek veikta galīgā permutācija (FP).
- Šī procesa rezultāts rada 64 bitu šifrētu tekstu.
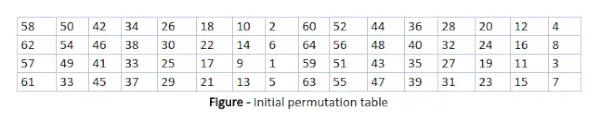
Sākotnējā permutācija (IP)
Kā mēs atzīmējām, sākotnējā permutācija (IP) notiek tikai vienu reizi, un tā notiek pirms pirmās kārtas. Tajā ir norādīts, kā būtu jāturpina transponēšana IP, kā parādīts attēlā. Piemēram, tajā ir teikts, ka IP aizstāj sākotnējā vienkāršā teksta bloka pirmo bitu ar oriģinālā vienkāršā teksta 58. bitu, otro bitu ar sākotnējā vienkāršā teksta bloka 50. bitu un tā tālāk.
Tas nav nekas cits kā sākotnējā vienkāršā teksta bloka bitu pozīciju žonglēšana. tas pats noteikums attiecas uz visām pārējām bitu pozīcijām, kas parādītas attēlā.
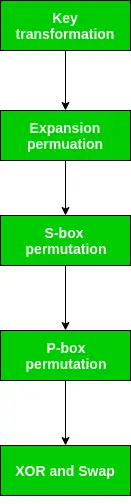
Kā mēs atzīmējām pēc IP pabeigšanas, iegūtais 64 bitu permutētais teksta bloks ir sadalīts divos pusblokos. Katrs pusbloks sastāv no 32 bitiem, un katrs no 16 kārtām, savukārt, sastāv no plaša līmeņa soļiem, kas norādīti attēlā.
1. darbība: atslēgas pārveidošana
Mēs esam ievērojuši, ka sākotnējā 64 bitu atslēga tiek pārveidota par 56 bitu atslēgu, atmetot katru sākotnējās atslēgas 8. bitu. Tādējādi katram ir pieejama 56 bitu atslēga. No šīs 56 bitu atslēgas katras kārtas laikā tiek ģenerēta cita 48 bitu apakšatslēga, izmantojot procesu, ko sauc par atslēgas pārveidošanu. Šim nolūkam 56 bitu atslēga ir sadalīta divās daļās, katra no 28 bitiem. Šīs pusītes ir apļveida nobīdes pa kreisi par vienu vai divām pozīcijām atkarībā no kārtas.
Piemēram: ja kārtas skaitļi 1, 2, 9 vai 16, pārejām kārtām tiek veikta tikai viena pozīcija, apļveida nobīde tiek veikta par divām pozīcijām. Atslēgas bitu skaits, kas nobīdīts vienā kārtā, ir parādīts attēlā.

Pēc atbilstošas maiņas tiek atlasīti 48 no 56 bitiem. No 48 mēs varam iegūt 64 vai 56 bitus, pamatojoties uz prasībām, kas palīdz mums atpazīt, ka šis modelis ir ļoti daudzpusīgs un spēj izpildīt jebkuru nepieciešamo vai nodrošināto prasību klāstu. lai izvēlētos 48 no 56 bitiem, tabula ir parādīta attēlā zemāk. Piemēram, pēc maiņas bits numurs 14 tiek pārvietots uz pirmo pozīciju, bits numurs 17 tiek pārvietots uz otro pozīciju un tā tālāk. Ja mēs novērojam tabulu, mēs sapratīsim, ka tajā ir tikai 48 bitu pozīcijas. 18. bits tiek atmests (tabulā mēs to neatradīsim), tāpat kā 7 bitu, lai 56 bitu atslēgu samazinātu uz 48 bitu atslēgu. Tā kā atslēgas pārveidošanas process ietver permutāciju, kā arī sākotnējās 56 bitu atslēgas 48 bitu apakškopas atlasi, to sauc par kompresijas permutāciju.
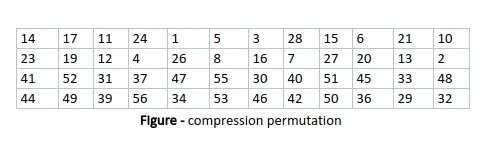
Šīs saspiešanas permutācijas metodes dēļ katrā kārtā tiek izmantota cita atslēgu bitu apakškopa. Tāpēc DES nav viegli uzlauzt.
2. darbība: paplašināšanas permutācija
Atgādiniet, ka pēc sākotnējās permutācijas mums bija divi 32 bitu vienkārša teksta apgabali, ko sauca par kreiso vienkāršu tekstu (LPT) un labo vienkāršu tekstu (RPT). Paplašināšanas permutācijas laikā RPT tiek paplašināts no 32 bitiem līdz 48 bitiem. Biti ir arī permutēti, tāpēc tos sauc par paplašināšanas permutāciju. Tas notiek, jo 32 bitu RPT ir sadalīts 8 blokos, un katrs bloks sastāv no 4 bitiem. Pēc tam katrs iepriekšējā soļa 4 bitu bloks tiek paplašināts līdz atbilstošam 6 bitu blokam, t.i., katram 4 bitu blokam tiek pievienoti vēl 2 biti.
kā virkni pārvērst int
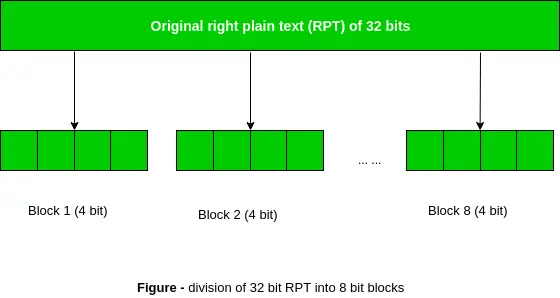
Šī procesa rezultātā tiek paplašināts, kā arī tiek mainīts ievades bits, vienlaikus veidojot izvadi. Atslēgas pārveidošanas process saspiež 56 bitu atslēgu līdz 48 bitiem. Tad paplašināšanas permutācijas process paplašina 32 bitu RPT uz 48 biti . Tagad ir 48 bitu atslēga BEZMAKSAS ar 48 bitu RPT, un iegūtā izvade tiek nodota nākamajam solim, kas ir S-box aizstāšana .
Python
# Python3 code for the above approach> # Hexadecimal to binary conversion> def> hex2bin(s):> >mp>=> {>'0'>:>'0000'>,> >'1'>:>'0001'>,> >'2'>:>'0010'>,> >'3'>:>'0011'>,> >'4'>:>'0100'>,> >'5'>:>'0101'>,> >'6'>:>'0110'>,> >'7'>:>'0111'>,> >'8'>:>'1000'>,> >'9'>:>'1001'>,> >'A'>:>'1010'>,> >'B'>:>'1011'>,> >'C'>:>'1100'>,> >'D'>:>'1101'>,> >'E'>:>'1110'>,> >'F'>:>'1111'>}> >bin> => ''> >for> i>in> range>(>len>(s)):> >bin> => bin> +> mp[s[i]]> >return> bin> # Binary to hexadecimal conversion> def> bin2hex(s):> >mp>=> {>'0000'>:>'0'>,> >'0001'>:>'1'>,> >'0010'>:>'2'>,> >'0011'>:>'3'>,> >'0100'>:>'4'>,> >'0101'>:>'5'>,> >'0110'>:>'6'>,> >'0111'>:>'7'>,> >'1000'>:>'8'>,> >'1001'>:>'9'>,> >'1010'>:>'A'>,> >'1011'>:>'B'>,> >'1100'>:>'C'>,> >'1101'>:>'D'>,> >'1110'>:>'E'>,> >'1111'>:>'F'>}> >hex> => ''> >for> i>in> range>(>0>,>len>(s),>4>):> >ch>=> ''> >ch>=> ch>+> s[i]> >ch>=> ch>+> s[i>+> 1>]> >ch>=> ch>+> s[i>+> 2>]> >ch>=> ch>+> s[i>+> 3>]> >hex> => hex> +> mp[ch]> >return> hex> # Binary to decimal conversion> def> bin2dec(binary):> >binary1>=> binary> >decimal, i, n>=> 0>,>0>,>0> >while>(binary !>=> 0>):> >dec>=> binary>%> 10> >decimal>=> decimal>+> dec>*> pow>(>2>, i)> >binary>=> binary>/>/>10> >i>+>=> 1> >return> decimal> # Decimal to binary conversion> def> dec2bin(num):> >res>=> bin>(num).replace(>'0b'>, '')> >if>(>len>(res)>%> 4> !>=> 0>):> >div>=> len>(res)>/> 4> >div>=> int>(div)> >counter>=> (>4> *> (div>+> 1>))>-> len>(res)> >for> i>in> range>(>0>, counter):> >res>=> '0'> +> res> >return> res> # Permute function to rearrange the bits> def> permute(k, arr, n):> >permutation>=> ''> >for> i>in> range>(>0>, n):> >permutation>=> permutation>+> k[arr[i]>-> 1>]> >return> permutation> # shifting the bits towards left by nth shifts> def> shift_left(k, nth_shifts):> >s>=> ''> >for> i>in> range>(nth_shifts):> >for> j>in> range>(>1>,>len>(k)):> >s>=> s>+> k[j]> >s>=> s>+> k[>0>]> >k>=> s> >s>=> ''> >return> k> # calculating xow of two strings of binary number a and b> def> xor(a, b):> >ans>=> ''> >for> i>in> range>(>len>(a)):> >if> a[i]>=>=> b[i]:> >ans>=> ans>+> '0'> >else>:> >ans>=> ans>+> '1'> >return> ans> # Table of Position of 64 bits at initial level: Initial Permutation Table> initial_perm>=> [>58>,>50>,>42>,>34>,>26>,>18>,>10>,>2>,> >60>,>52>,>44>,>36>,>28>,>20>,>12>,>4>,> >62>,>54>,>46>,>38>,>30>,>22>,>14>,>6>,> >64>,>56>,>48>,>40>,>32>,>24>,>16>,>8>,> >57>,>49>,>41>,>33>,>25>,>17>,>9>,>1>,> >59>,>51>,>43>,>35>,>27>,>19>,>11>,>3>,> >61>,>53>,>45>,>37>,>29>,>21>,>13>,>5>,> >63>,>55>,>47>,>39>,>31>,>23>,>15>,>7>]> # Expansion D-box Table> exp_d>=> [>32>,>1>,>2>,>3>,>4>,>5>,>4>,>5>,> >6>,>7>,>8>,>9>,>8>,>9>,>10>,>11>,> >12>,>13>,>12>,>13>,>14>,>15>,>16>,>17>,> >16>,>17>,>18>,>19>,>20>,>21>,>20>,>21>,> >22>,>23>,>24>,>25>,>24>,>25>,>26>,>27>,> >28>,>29>,>28>,>29>,>30>,>31>,>32>,>1>]> # Straight Permutation Table> per>=> [>16>,>7>,>20>,>21>,> >29>,>12>,>28>,>17>,> >1>,>15>,>23>,>26>,> >5>,>18>,>31>,>10>,> >2>,>8>,>24>,>14>,> >32>,>27>,>3>,>9>,> >19>,>13>,>30>,>6>,> >22>,>11>,>4>,>25>]> # S-box Table> sbox>=> [[[>14>,>4>,>13>,>1>,>2>,>15>,>11>,>8>,>3>,>10>,>6>,>12>,>5>,>9>,>0>,>7>],> >[>0>,>15>,>7>,>4>,>14>,>2>,>13>,>1>,>10>,>6>,>12>,>11>,>9>,>5>,>3>,>8>],> >[>4>,>1>,>14>,>8>,>13>,>6>,>2>,>11>,>15>,>12>,>9>,>7>,>3>,>10>,>5>,>0>],> >[>15>,>12>,>8>,>2>,>4>,>9>,>1>,>7>,>5>,>11>,>3>,>14>,>10>,>0>,>6>,>13>]],> >[[>15>,>1>,>8>,>14>,>6>,>11>,>3>,>4>,>9>,>7>,>2>,>13>,>12>,>0>,>5>,>10>],> >[>3>,>13>,>4>,>7>,>15>,>2>,>8>,>14>,>12>,>0>,>1>,>10>,>6>,>9>,>11>,>5>],> >[>0>,>14>,>7>,>11>,>10>,>4>,>13>,>1>,>5>,>8>,>12>,>6>,>9>,>3>,>2>,>15>],> >[>13>,>8>,>10>,>1>,>3>,>15>,>4>,>2>,>11>,>6>,>7>,>12>,>0>,>5>,>14>,>9>]],> >[[>10>,>0>,>9>,>14>,>6>,>3>,>15>,>5>,>1>,>13>,>12>,>7>,>11>,>4>,>2>,>8>],> >[>13>,>7>,>0>,>9>,>3>,>4>,>6>,>10>,>2>,>8>,>5>,>14>,>12>,>11>,>15>,>1>],> >[>13>,>6>,>4>,>9>,>8>,>15>,>3>,>0>,>11>,>1>,>2>,>12>,>5>,>10>,>14>,>7>],> >[>1>,>10>,>13>,>0>,>6>,>9>,>8>,>7>,>4>,>15>,>14>,>3>,>11>,>5>,>2>,>12>]],> >[[>7>,>13>,>14>,>3>,>0>,>6>,>9>,>10>,>1>,>2>,>8>,>5>,>11>,>12>,>4>,>15>],> >[>13>,>8>,>11>,>5>,>6>,>15>,>0>,>3>,>4>,>7>,>2>,>12>,>1>,>10>,>14>,>9>],> >[>10>,>6>,>9>,>0>,>12>,>11>,>7>,>13>,>15>,>1>,>3>,>14>,>5>,>2>,>8>,>4>],> >[>3>,>15>,>0>,>6>,>10>,>1>,>13>,>8>,>9>,>4>,>5>,>11>,>12>,>7>,>2>,>14>]],> >[[>2>,>12>,>4>,>1>,>7>,>10>,>11>,>6>,>8>,>5>,>3>,>15>,>13>,>0>,>14>,>9>],> >[>14>,>11>,>2>,>12>,>4>,>7>,>13>,>1>,>5>,>0>,>15>,>10>,>3>,>9>,>8>,>6>],> >[>4>,>2>,>1>,>11>,>10>,>13>,>7>,>8>,>15>,>9>,>12>,>5>,>6>,>3>,>0>,>14>],> >[>11>,>8>,>12>,>7>,>1>,>14>,>2>,>13>,>6>,>15>,>0>,>9>,>10>,>4>,>5>,>3>]],> >[[>12>,>1>,>10>,>15>,>9>,>2>,>6>,>8>,>0>,>13>,>3>,>4>,>14>,>7>,>5>,>11>],> >[>10>,>15>,>4>,>2>,>7>,>12>,>9>,>5>,>6>,>1>,>13>,>14>,>0>,>11>,>3>,>8>],> >[>9>,>14>,>15>,>5>,>2>,>8>,>12>,>3>,>7>,>0>,>4>,>10>,>1>,>13>,>11>,>6>],> >[>4>,>3>,>2>,>12>,>9>,>5>,>15>,>10>,>11>,>14>,>1>,>7>,>6>,>0>,>8>,>13>]],> >[[>4>,>11>,>2>,>14>,>15>,>0>,>8>,>13>,>3>,>12>,>9>,>7>,>5>,>10>,>6>,>1>],> >[>13>,>0>,>11>,>7>,>4>,>9>,>1>,>10>,>14>,>3>,>5>,>12>,>2>,>15>,>8>,>6>],> >[>1>,>4>,>11>,>13>,>12>,>3>,>7>,>14>,>10>,>15>,>6>,>8>,>0>,>5>,>9>,>2>],> >[>6>,>11>,>13>,>8>,>1>,>4>,>10>,>7>,>9>,>5>,>0>,>15>,>14>,>2>,>3>,>12>]],> >[[>13>,>2>,>8>,>4>,>6>,>15>,>11>,>1>,>10>,>9>,>3>,>14>,>5>,>0>,>12>,>7>],> >[>1>,>15>,>13>,>8>,>10>,>3>,>7>,>4>,>12>,>5>,>6>,>11>,>0>,>14>,>9>,>2>],> >[>7>,>11>,>4>,>1>,>9>,>12>,>14>,>2>,>0>,>6>,>10>,>13>,>15>,>3>,>5>,>8>],> >[>2>,>1>,>14>,>7>,>4>,>10>,>8>,>13>,>15>,>12>,>9>,>0>,>3>,>5>,>6>,>11>]]]> # Final Permutation Table> final_perm>=> [>40>,>8>,>48>,>16>,>56>,>24>,>64>,>32>,> >39>,>7>,>47>,>15>,>55>,>23>,>63>,>31>,> >38>,>6>,>46>,>14>,>54>,>22>,>62>,>30>,> >37>,>5>,>45>,>13>,>53>,>21>,>61>,>29>,> >36>,>4>,>44>,>12>,>52>,>20>,>60>,>28>,> >35>,>3>,>43>,>11>,>51>,>19>,>59>,>27>,> >34>,>2>,>42>,>10>,>50>,>18>,>58>,>26>,> >33>,>1>,>41>,>9>,>49>,>17>,>57>,>25>]> def> encrypt(pt, rkb, rk):> >pt>=> hex2bin(pt)> ># Initial Permutation> >pt>=> permute(pt, initial_perm,>64>)> >print>(>'After initial permutation'>, bin2hex(pt))> ># Splitting> >left>=> pt[>0>:>32>]> >right>=> pt[>32>:>64>]> >for> i>in> range>(>0>,>16>):> ># Expansion D-box: Expanding the 32 bits data into 48 bits> >right_expanded>=> permute(right, exp_d,>48>)> ># XOR RoundKey[i] and right_expanded> >xor_x>=> xor(right_expanded, rkb[i])> ># S-boxex: substituting the value from s-box table by calculating row and column> >sbox_str>=> ''> >for> j>in> range>(>0>,>8>):> >row>=> bin2dec(>int>(xor_x[j>*> 6>]>+> xor_x[j>*> 6> +> 5>]))> >col>=> bin2dec(> >int>(xor_x[j>*> 6> +> 1>]>+> xor_x[j>*> 6> +> 2>]>+> xor_x[j>*> 6> +> 3>]>+> xor_x[j>*> 6> +> 4>]))> >val>=> sbox[j][row][col]> >sbox_str>=> sbox_str>+> dec2bin(val)> ># Straight D-box: After substituting rearranging the bits> >sbox_str>=> permute(sbox_str, per,>32>)> ># XOR left and sbox_str> >result>=> xor(left, sbox_str)> >left>=> result> ># Swapper> >if>(i !>=> 15>):> >left, right>=> right, left> >print>(>'Round '>, i>+> 1>,>' '>, bin2hex(left),> >' '>, bin2hex(right),>' '>, rk[i])> ># Combination> >combine>=> left>+> right> ># Final permutation: final rearranging of bits to get cipher text> >cipher_text>=> permute(combine, final_perm,>64>)> >return> cipher_text> pt>=> '123456ABCD132536'> key>=> 'AABB09182736CCDD'> # Key generation> # --hex to binary> key>=> hex2bin(key)> # --parity bit drop table> keyp>=> [>57>,>49>,>41>,>33>,>25>,>17>,>9>,> >1>,>58>,>50>,>42>,>34>,>26>,>18>,> >10>,>2>,>59>,>51>,>43>,>35>,>27>,> >19>,>11>,>3>,>60>,>52>,>44>,>36>,> >63>,>55>,>47>,>39>,>31>,>23>,>15>,> >7>,>62>,>54>,>46>,>38>,>30>,>22>,> >14>,>6>,>61>,>53>,>45>,>37>,>29>,> >21>,>13>,>5>,>28>,>20>,>12>,>4>]> # getting 56 bit key from 64 bit using the parity bits> key>=> permute(key, keyp,>56>)> # Number of bit shifts> shift_table>=> [>1>,>1>,>2>,>2>,> >2>,>2>,>2>,>2>,> >1>,>2>,>2>,>2>,> >2>,>2>,>2>,>1>]> # Key- Compression Table : Compression of key from 56 bits to 48 bits> key_comp>=> [>14>,>17>,>11>,>24>,>1>,>5>,> >3>,>28>,>15>,>6>,>21>,>10>,> >23>,>19>,>12>,>4>,>26>,>8>,> >16>,>7>,>27>,>20>,>13>,>2>,> >41>,>52>,>31>,>37>,>47>,>55>,> >30>,>40>,>51>,>45>,>33>,>48>,> >44>,>49>,>39>,>56>,>34>,>53>,> >46>,>42>,>50>,>36>,>29>,>32>]> # Splitting> left>=> key[>0>:>28>]># rkb for RoundKeys in binary> right>=> key[>28>:>56>]># rk for RoundKeys in hexadecimal> rkb>=> []> rk>=> []> for> i>in> range>(>0>,>16>):> ># Shifting the bits by nth shifts by checking from shift table> >left>=> shift_left(left, shift_table[i])> >right>=> shift_left(right, shift_table[i])> ># Combination of left and right string> >combine_str>=> left>+> right> ># Compression of key from 56 to 48 bits> >round_key>=> permute(combine_str, key_comp,>48>)> >rkb.append(round_key)> >rk.append(bin2hex(round_key))> print>(>'Encryption'>)> cipher_text>=> bin2hex(encrypt(pt, rkb, rk))> print>(>'Cipher Text : '>, cipher_text)> print>(>'Decryption'>)> rkb_rev>=> rkb[::>->1>]> rk_rev>=> rk[::>->1>]> text>=> bin2hex(encrypt(cipher_text, rkb_rev, rk_rev))> print>(>'Plain Text : '>, text)> # This code is contributed by Aditya Jain> |
>
>
Javascript
java pgm
// Define DES key and plaintext> const key =>'0123456789abcdef'>;> const plaintext =>'Hello, world!'>;> // Perform DES encryption> const des =>new> DES(key);> const ciphertext = des.encrypt(plaintext);> // Perform DES decryption> const decrypted = des.decrypt(ciphertext);> // Print results> console.log(>'Plaintext: '>, plaintext);> console.log(>'Ciphertext: '>, ciphertext);> console.log(>'Decrypted: '>, decrypted);> // Define DES class> class DES {> >constructor(key) {> >// Initialize DES with key> >this>.key = CryptoJS.enc.Hex.parse(key);> >}> >encrypt(plaintext) {> >// Perform DES encryption on plaintext> >const encrypted = CryptoJS.DES.encrypt(> >plaintext,> >this>.key,> >{ mode: CryptoJS.mode.ECB }> >);> >// Return ciphertext as hex string> >return> encrypted.ciphertext.toString();> >}> >decrypt(ciphertext) {> >// Parse ciphertext from hex string> >const ciphertextHex = CryptoJS.enc.Hex.parse(ciphertext);> >// Perform DES decryption on ciphertext> >const decrypted = CryptoJS.DES.decrypt(> >{ ciphertext: ciphertextHex },> >this>.key,> >{ mode: CryptoJS.mode.ECB }> >);> >// Return decrypted plaintext as UTF-8 string> >return> decrypted.toString(CryptoJS.enc.Utf8);> >}> }> |
>
>Izvade
...60AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536>
Izvade:
java pievienot masīvam
Encryption: After initial permutation: 14A7D67818CA18AD After splitting: L0=14A7D678 R0=18CA18AD Round 1 18CA18AD 5A78E394 194CD072DE8C Round 2 5A78E394 4A1210F6 4568581ABCCE Round 3 4A1210F6 B8089591 06EDA4ACF5B5 Round 4 B8089591 236779C2 DA2D032B6EE3 Round 5 236779C2 A15A4B87 69A629FEC913 Round 6 A15A4B87 2E8F9C65 C1948E87475E Round 7 2E8F9C65 A9FC20A3 708AD2DDB3C0 Round 8 A9FC20A3 308BEE97 34F822F0C66D Round 9 308BEE97 10AF9D37 84BB4473DCCC Round 10 10AF9D37 6CA6CB20 02765708B5BF Round 11 6CA6CB20 FF3C485F 6D5560AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536>
Secinājums
Noslēgumā jāsaka, ka datu šifrēšanas standarts (DES) ir a bloķēt šifru ar 56 bitu atslēgas garumu, kam ir bijusi nozīmīga loma datu drošībā. Tomēr ievainojamības dēļ tā popularitāte ir samazinājusies. DES darbojas, izmantojot vairākas kārtas, kas ietver atslēgu transformāciju, paplašināšanas permutāciju un aizstāšanu, galu galā veidojot šifrētu tekstu no vienkārša teksta. Lai gan DES ir vēsturiska nozīme, ir svarīgi apsvērt drošāku šifrēšana alternatīvas mūsdienu datu aizsardzības vajadzībām.
bieži uzdotie jautājumi
Q.1 : Kas būtu jāuzskata par alternatīvu DES datu šifrēšanai?
Atbilde:
Mūsdienu datu šifrēšanas vajadzībām apsveriet iespēju izmantot spēcīgākus šifrēšanas algoritmus, piemēram, AES (Uzlabots šifrēšanas standarts).
Q.2 : Kā DES katrai kārtai tiek ģenerēta 48 bitu apakšatslēga?
Atbilde:
48 bitu apakšatslēga katrai DES kārtai tiek iegūta no 56 bitu atslēgas, izmantojot apļveida nobīdes un permutācijas procesu, nodrošinot atslēgu dažādību.

