KOTANGENTES FORMULA

Trigonometrija ir svarīga matemātikas nozare, kas nodarbojas ar attiecību starp taisnleņķa trīsstūra malu garumiem un leņķiem. Sinuss, kosinuss, tangenss, kosekants, sekants un kotangenss ir sešas trigonometriskās attiecības vai funkcijas. Kur trigonometriskā attiecība ir attēlota kā attiecība starp taisnleņķa trīsstūra malām.

sin θ = pretējā puse/hipotenūza
cos θ = blakus esošā puse/hipotenūza
iedegums θ = pretējā puse/blakuspuse
cosec θ = 1/sin θ = hipotenūza/pretējā puse
sec θ = 1/cos θ = hipotenūza/blakuspuse
gultiņa θ = 1/iedegums θ = blakus puse/pretējā puse

Kotangentes funkcija ir dotās pieskares funkcijas abpusēja funkcija. Kotangences leņķa vērtība taisnleņķa trijstūrī ir dotajam leņķim blakus esošās malas garuma attiecība pret dotajam leņķim pretējās malas garumu. Mēs rakstām kotangentes funkciju kā bērnu gultiņa.

Trīsstūris ABC

Tagad leņķa θ kotangences formula ir,

bērnu gultiņa θ = (blakus esošā puse)/(pretējā puse)

Kotangences funkcija ir pozitīva pirmajā un trešajā kvadrantā un negatīva otrajā un ceturtajā kvadrantā.

gultiņa (2π + θ) = bērnu gultiņa θ (1^stkvadrants)
bērnu gultiņa (π – θ) = – gultiņa θ (2^ndkvadrants)
gultiņa (π + θ) = bērnu gultiņa θ (3^rdkvadrants)
bērnu gultiņa (2π – θ) = – gultiņa θ (4^thkvadrants)

Kotangenses funkcija ir negatīva funkcija, jo negatīvā leņķa kotangenss ir negatīvā kotangences pozitīvā leņķa.

gultiņa (-θ) = – gultiņa θ

Runājot par pieskares funkciju, kotangentes funkcija ir uzrakstīta kā,

bērnu gultiņa θ = 1/tan θ

(vai)

gultiņa θ = iedegums (90° – θ) (vai) iedegums (π/2 – θ)

Kotangentes funkciju sinusa un kosinusa funkciju izteiksmē var uzrakstīt kā,

gultiņa θ = cos θ/sin θ

Mēs zinām, ka gultiņa θ = blakus esošā puse/pretējā puse

Tagad sadaliet gan skaitītāju, gan saucēju ar hipotenūzu

⇒ bērnu gultiņa θ = (blakuspuse/hipotenūza) / (pretējā puse/hipotenūza)

Mēs zinām, ka grēks θ = pretējā puse/hipotenūza

cos θ = blakus esošā puse/hipotenūza
java savienojošās virknes

Tādējādi gultiņa θ = cos θ/sin θ

Kotangentes funkciju sinusa funkcijas izteiksmē var uzrakstīt kā,

gultiņa θ = (√1 – grēks ² i)/grēks i

Mēs zinām, ka cot θ = cos θ/sin θ

No Pitagora identitātēm, kas mums ir;

cos²θ + grēks²θ = 1

⇒ cos θ = √1 – grēks²i

Tādējādi bērnu gultiņa θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

Kotangentes funkciju kosinusa funkcijas izteiksmē var uzrakstīt kā,

gultiņa θ = cos θ/(√1 -cos ² i)

Mēs zinām, ka cot θ = cos θ/sin θ

No Pitagora identitātēm, kas mums ir;

cos²θ + grēks²θ = 1

sin θ = √1 – cos²i

Tādējādi bērnu gultiņa θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

Kotangentes funkciju sekantu un kosekantu funkciju izteiksmē var uzrakstīt kā,

gultiņa θ = cosec θ/sec θ

Mums ir, gultiņa θ = cos θ/sin θ

To var uzrakstīt šādi: cot θ = (1/sin θ) / (1/cos θ)

⇒ gultiņa θ = cosec θ/sec θ

Kotangentes funkciju kosekantu funkcijas izteiksmē var uzrakstīt šādi:

bērnu gultiņa θ = √ (kosek ² - 1)

No Pitagora identitātēm mums ir,

cosec²θ – bērnu gultiņa²θ = 1

⇒ bērnu gultiņa²θ = 1 – kosek²- 1

Tādējādi bērnu gultiņa θ = √ (kosek²- 1)

Kotangentes funkciju secant funkcijas izteiksmē var uzrakstīt šādi:

gultiņa θ = 1/(√s ² es - 1)

No Pitagora identitātēm mums ir,

sek²θ – tātad²θ = 1

iedegums θ = √sek²es - 1

Mēs zinām, ka gultiņa θ = 1/tan θ

Tāpēc gultiņa θ = $frac{1}{sqrt{left(1-sec^{2} heta ight)}}$

Trigonometrisko attiecību tabula

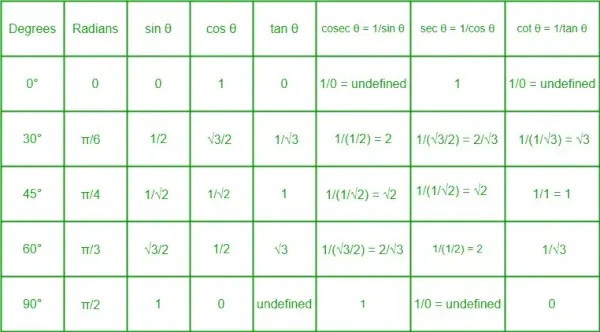
Trigonometrisko attiecību tabula

Kotangensu likums vai kotangentu likums

Kotangences likums izskatās līdzīgs sinusa likumam, bet šeit tas ietver pusleņķus. Kotangensu likums apraksta attiecības starp trijstūra malu garumiem un trīs leņķu pušu kotangentēm. Aplūkosim trīsstūri ABC, kur a, b un c ir trijstūra malu garumi.

Kotangensu likums nosaka, ka

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

Kur s ir trijstūra ABC pusperimetrs un r ir tā trijstūra ierakstītā riņķa rādiuss.

s = (a + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

Problēmu paraugi

1. uzdevums: atrodiet gultiņas θ vērtību, ja iedegums θ = 3/4.

Risinājums:

Dotajos datos tan θ = 3/4

Mēs to zinām, bērnu gultiņa θ = 1/tan θ

⇒ bērnu gultiņa θ = 1/(3/4) = 4/3

Tātad, bērnu gultiņa θ = 4/3

2. uzdevums. Atrodiet cot α vērtību, sin α = 1/3 un cos α = 2√2/3.

java sarakstu uz masīvu

Risinājums:

Dotajos datos sin α = 1/3 un cos α = 2√2/3

Mēs to zinām, gultiņa α = cos α/sin α

⇒ bērnu gultiņa α = (2√2/3) / (1/3) = 2√2

Tādējādi bērnu gultiņas vērtība α = 2√2

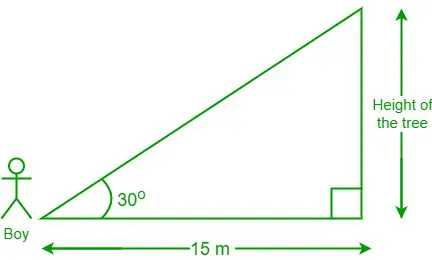
3. problēma: zēns, kurš stāv 15 m attālumā no koka, skatās 30 grādu leņķī pret koka galotni. Kāds ir koka augstums?

Risinājums:

Diagramma no dotajiem datiem

Dotie dati, attālums starp zēnu un koka pēdu = 15 m un θ = 30°

Lai koka augstums ir “h”

Mums ir, gultiņa θ = blakus esošā puse/pretējā puse

⇒ bērnu gultiņa 30° = 15/h

⇒ √3 = 15/h [kopš, bērnu gultiņa 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3 m

Tātad koka augstums = 5√3 m

4. uzdevums: atrodiet gultiņas x vērtību, ja sec x = 6/5.

Risinājums:

Dotie dati, sek x = 6/5

Mums ir, sek ² x - tā ² x = 1

⇒ (6/5)²- tātad²x = 1

⇒ 36/25 – tātad²x = 1

⇒ tā²x = 36/25 – 1

⇒ tā²x = 11/25

⇒ iedegums x = √(11/25) = √11/5

Mēs to zinām, gultiņa x = 1/iedegums x

⇒ bērnu gultiņa x = 1/(√11/5) = 5/√11

Tādējādi bērnu gultiņa x = 5/√11

5. uzdevums: atrodiet gultiņas θ vērtību, ja cosec θ = 25/24.

Risinājums:

Dotie dati, cosec θ = 25/24

Mēs to zinām, bērnu gultiņa θ = √ (kosek ² - 1)

⇒ bērnu gultiņa θ = √(25/24)²- 1

⇒ bērnu gultiņa θ =√(625–576)/576 = √49/576

⇒ bērnu gultiņa θ = 7/24

Tādējādi bērnu gultiņas vērtība θ = 7/24

6. uzdevums: atrodiet gultiņas β vērtību, ja sin β = 5/13.

Risinājums:

Dotajiem datiem grēks β = 5/13

Mēs to zinām, bez ² β + cos ² β = 1
virkne līdz veselam skaitlim

⇒ (5/13)²+ cos²β = 1

⇒ cos²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cos β = √144/169 = 12/13

gultiņa β = cosβ/sin β

= (12/13) / (5/13)

⇒ bērnu gultiņa β = 12/5

Tādējādi bērnu gultiņas vērtība β = 12/5

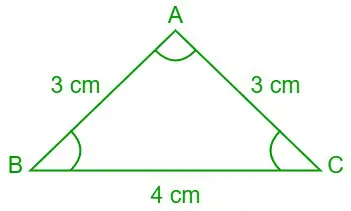
7. uzdevums. Izmantojot kotangenšu likumu, atrodiet ∠A, ∠B un ∠C vērtības (grādos), ja trīsstūra ABC trīs malu garumi ir a = 4 cm, b= 3 cm un c= 3 cm.

Risinājums:

Ņemot vērā, ka a = 4 cm, b = 3 cm un c = 3 cm

Trīsstūris ABC

No kotangensu likuma

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Tagad s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1) (2) (2)/5]

Trijstūra rādiuss r = 2/√5

No kotangensu likuma vienādojuma,

bērnu gultiņa (A/2)/1 = 1/(2/√5)

⇒ bērnu gultiņa (A/2) = √5/2 ⇒ A/2 = bērnu gultiņa^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

bērnu gultiņa (B/2)/2 = 1/(2/√5)

⇒ bērnu gultiņa (B/2)/2 = √5/2 ⇒ bērnu gultiņa (B/2) = √5

⇒ (B/2) = bērnu gultiņa^-1(√5) = 24,1° ⇒ ∠B = 48,2°

bērnu gultiņa (C/2)/2 = 1/(2/√5)

⇒ gultiņa (C/2) = √5 ⇒ (C/2) = bērnu gultiņa^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

Tādējādi trīsstūra ABC leņķi ir ∠A = 83,6°, ∠B = 48,2° un ∠C = 48,2°.