Paātrinājums ir ātruma izmaiņas laika gaitā. Reālajā dzīvē paātrinājums arī mainās ar laiku. Piemēram, jūs ceļojat no vienas pilsētas uz citu pilsētu pa autoceļiem. Tad šajā gadījumā jūs paātrināsit vairāk tukša ceļa gadījumā un paātrināsiet uz leju satiksmes gadījumā. Šīs paātrinājuma izmaiņas var novērot, grafikā attēlojot paātrinājumu pret laiku. To sauc par paātrinājuma laika grafiku. Šajā rakstā mēs detalizēti uzzināsim par paātrinājuma laika grafiku un atrisināsim problēmas, pamatojoties uz to.
ievietošanas šķirošanas algoritmi
Kas ir paātrinājuma laika diagramma?
Paātrinājuma laika grafiks tiek izmantots, lai attēlotu attiecības starp paātrinājums un laiks, kur paātrinājums ir neatkarīgs mainīgais, kas attēlots uz Y ass, un laiks ir atkarīgs mainīgais, kas attēlots uz X ass. To iegūst, kad iegūtos paātrinājuma un laika datus attēlo taisnstūrveida grafikā, pētot ķermeņa kustību. Ātruma izmaiņas noteiktā laika intervālā varam noteikt ar paātrinājuma-laika grafika palīdzību. Nosakot laukumu zem paātrinājuma-laika grafika līknes, mēs varam atrast kustībā esoša objekta ātruma izmaiņas noteiktā laika periodā.
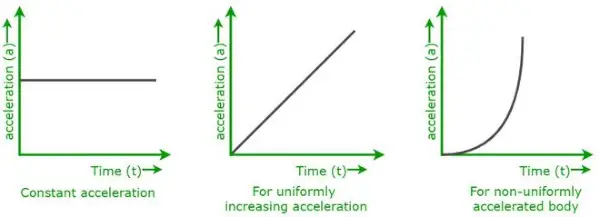
Iepriekš parādītie grafiki ir paātrinājuma laika grafiki dažāda veida ķermeņa kustībām.
- Kad ķermenis kustas ar pastāvīgu paātrinājumu,
- Kad ķermenis pārvietojas vienmērīgi, palielinoties paātrinājumam.
- Kad ķermenis pārvietojas nevienmērīgi ar mainīgu paātrinājumu.
Secinājumi
Tālāk ir norādīti punkti, kas iegūti no paātrinājuma laika grafikiem.
- Paātrinājuma un laika grafika slīpums ir △a/△t.
- Laukums zem paātrinājuma laika grafika attēlo ātruma izmaiņas.
Ļaujiet,
△ v būt ātruma izmaiņām,
△a būt paātrinājuma izmaiņām,
△ t būt laika maiņai.
Tagad laukums zem līknes = △v
Mēs zinām, ka ķermeņa paātrinājumu sauc par ātruma izmaiņu ātrumu noteiktā laika periodā.
Tātad,
△a = △v/△t
Tagad, reizinot ar △t abās pusēs, mēs iegūstam,
△v = △a × △t (v tas ir laukums zem līknes paātrinājuma laikā grafikā )
- Objektam, kas pārvietojas ar pastāvīgu paātrinājumu, t.i., paātrinājums visos laika intervālos ir vienāds. Tādējādi paātrinājuma un laika grafika slīpums ir nulle, un grafiks būs paralēls laika asij.
Paātrinājums pret aizkavēšanos

Paātrinājums: Ķermeņa paātrinājumu sauc par ātruma izmaiņu ātrumu noteiktā laika periodā. Tas ir vektora lielums, un to mēra m/s2.
Paātrinājums = ātruma/laika izmaiņas
šeit ātruma izmaiņas ir pozitīvas.
Pieņemsim, ka ķermenis, kas pārvietojas ar vienmērīgu ātrumu, palielina savu ātrumu. Ātruma pieauguma ātrumu sauc par ķermeņa paātrinājumu. Lai u ir sākotnējais ātrums, v ir gala ātrums un t ir laika intervāls, tad ķermeņa paātrinājums tiek dots kā,
Paātrinājums (a) = (v – u)/t
Piemērs: Paātrinājuma piemērs ikdienā ir automašīnas pagriešana līkumā. Automašīnas ātrums palielinās, mainoties virzienam, kā rezultātā notiek paātrinājums. Paātrinājums palielinās, palielinoties pagrieziena ātrumam.
Atpalicība: Ķermeņa aizkavēšanos sauc par ātruma izmaiņu ātrumu noteiktā laika periodā. Atpalicība nozīmē negatīvu paātrinājumu.
Retardācija = ātruma/laika izmaiņas
šeit ātruma izmaiņas ir negatīvas.
Pieņemsim, ka ķermenis, kas pārvietojas ar vienmērīgu ātrumu, samazina savu ātrumu. Ātruma samazināšanās ātrumu sauc par ķermeņa aizkavēšanos. Lai u ir sākotnējais ātrums, v ir gala ātrums un t ir laika intervāls, tad ķermeņa aizkavēšanās tiek dota kā,
Atpalicība = (v – u)/t
Piemērs: Dzīves atpalicības piemērs ir ventilatora izslēgšana. Kad kustīgā ventilatora slēdzis ir izslēgts, ventilatora lāpstiņu griešanās ātrums pakāpeniski palēninās. Šis ventilatora ātruma samazinājuma ātrums ir pazīstams kā aizkavēšanās.
Pārbaudiet arī šo:
- Attāluma laika grafiki
- Ātruma laika grafiki
Problēmu paraugi paātrinājuma laika diagrammās
1. problēma. No paātrinājuma un laika grafika, kas parādīts zemāk, nosakiet ātruma izmaiņas.

Risinājums:
Lai noteiktu ķermeņa ātruma izmaiņas, mums jānosaka laukums zem līknes.
Tātad, lai atrastu objekta ātruma izmaiņas, mums jāaprēķina trīsstūra laukums.
△v = trijstūra laukums
= ½ × 25 × 6
△v = 75 m/s.
Tādējādi ātruma izmaiņas ir 75 m/s.
2. uzdevums. No paātrinājuma un laika grafika, kas parādīts zemāk, atrodiet ķermeņa sākotnējo ātrumu, ja tā galīgais ātrums ir 55 m/sek.

Risinājums:
Lai noteiktu ķermeņa ātruma izmaiņas, mums jānosaka laukums zem līknes. No grafika mēs varam novērot, ka tam ir taisnstūris un trīsstūris. Tātad, lai atrastu objekta ātruma izmaiņas, mums jāaprēķina šo skaitļu laukums.
△v = trīsstūra laukums + taisnstūra laukums
= ½ × 8 × 6 + 2 × 8
△v = 24 + 16 = 42 m/s
Mēs to zinām,
△v = gala ātrums – sākuma ātrums
42 = 55 collasi
iekšāi= 55 – 42 = 13 m/s
Tādējādi sākotnējais ātrums ir 13 m/s.
3. uzdevums. No paātrinājuma un laika grafika, kas sniegts tālāk, nosakiet ātrumu pie t = 6 sek, ja v(0) = 0.

Risinājums:
Paātrinājumu dod;
a = dv/dt
⇒ dv = (a)dt
Integrējot abās pusēs, mēs iegūstam
∫dv = ∫(a) dt
⇒ v = ∫(1,5) dt
⇒ v(t) = 1,5t + c, kur c ir konstante
⇒ v(0) = 0
⇒ c = 0
Tagad v(t) = 1,5 t
v(6) = 1,5 × 6 = 9 m/s
Tādējādi ātrums pie t = 6 sek ir 9 m/s.
4. problēma: ko norāda laukums zem paātrinājuma laika grafika?
Risinājums:
Laukums zem paātrinājuma laika grafika attēlo ātruma izmaiņas.
Lai △v ir ātruma izmaiņas, △a ir paātrinājuma izmaiņas un △ nav izmaiņas laikā.
Tagad laukums zem līknes = △v
Mēs zinām, ka ķermeņa paātrinājumu sauc par ātruma izmaiņu attiecību noteiktā laika periodā.
Tātad,
△a = △v/△t
Tagad, reizinot ar △t abās pusēs, mēs iegūstam,
△v = △a × △t
Tātad laukumu zem līknes iegūst, reizinot paātrinājuma izmaiņas un izmaiņas laikā.
5. problēma: ko nozīmē saraustīšanās paātrinājuma laika grafikā?
Risinājums:
Saraustīšana ir pēkšņas izmaiņas kustīgā ķermeņa paātrinājumā, un a-t diagrammas slīpums atspoguļo grūdienu.
Paātrinājuma un laika grafika slīpums = raustīšanās = △a/△t
Paātrinājuma laika diagramma — FAQ
Kas ir paātrinājuma laika grafiks?
Paātrinājuma laika diagramma parāda, kā paātrinājums laika gaitā mainās objektam, kas pārvietojas pa taisnu līniju. Tas attēlo paātrinājumu uz y ass pret laiku uz x ass.
Kā aprēķināt laukumu zem paātrinājuma laika grafika un ko tas attēlo?
Laukums zem paātrinājuma laika grafika attēlo ātruma izmaiņas laika periodā, ko aptver grafiks. Lai aprēķinātu šo laukumu, parasti ir jāsaskaita to taisnstūru vai trapecveida laukumi, kas atrodas zem līknes, kas atbilst atšķirīgiem laika intervāliem, kuru laikā paātrinājums ir nemainīgs.
Vai jūs varat noteikt objekta ātrumu noteiktā laikā no paātrinājuma laika grafika?
Momentāno ātrumu noteiktā laikā tieši noteikt no paātrinājuma laika grafika nav iespējams. Tomēr jūs varat aprēķināt ātruma izmaiņas noteiktā laika periodā, šajā periodā atrodot apgabalu zem diagrammas. Zinot sākotnējo ātrumu, varat noteikt galīgo ātrumu.
Ko norāda negatīvs paātrinājums šāda veida grafikā?
Negatīvs paātrinājums paātrinājuma laika grafikā norāda palēninājumu, kur objekta ātrums samazinās, ja objekts pārvietojas pozitīvā virzienā. Ja objekts pārvietojas virzienā, kas tiek uzskatīts par negatīvu, tad negatīvs paātrinājums nozīmē ātruma palielināšanos.
Kā jūs varat atrast vidējo paātrinājumu no paātrinājuma laika grafika?
Vidējo paātrinājumu var noteikt, atrodot kopējās ātruma izmaiņas (summējot laukumus zem līknes, ņemot vērā virzienu) un dalot to ar kopējo laika intervālu. Vizuāli to var attēlot kā taisnstūri, kura laukums ir vienāds ar kopējo laukumu zem paātrinājuma laika grafika.
Ko attēlo paātrinājuma un laika grafika slīpums?
Paātrinājuma un laika diagrammas slīpums norāda paātrinājuma izmaiņu ātrumu laika gaitā, ko sauc par saraustīšanu. Stāvs slīpums nozīmē straujas paātrinājuma izmaiņas.
Kā attēlot miera stāvoklī esošu ķermeni paātrinājuma laika grafikā?
Ķermenis miera stāvoklī vai kustībā ar nemainīgu ātrumu ir attēlots paātrinājuma laika grafikā ar līniju gar laika asi pie nulles paātrinājuma.
Kā jūs interpretējat paātrinājuma laika grafiku?
Paātrinājuma laika diagrammas slīpums atspoguļo paātrinājuma izmaiņu ātrumu, kur stāvāks slīpums norāda uz lielāku izmaiņu ātrumu.
Ko attēlo laukums zem paātrinājuma laika grafika?
Laukums zem līknes paātrinājuma laika grafikā attēlo objekta ātruma izmaiņas. Konkrēti, tas apzīmē galīgo ātrumu mīnus sākotnējais ātrums.
